§2. Геометрический и физический смысл производной

Пусть – функция непрерывная на интервале , и – точки графика этой функции. Здесь

, Проведем через точки и секущую (см. рис.). Запишем уравнение секущей.

.

. (1)

Здесь

(2)

– угловой коэффициент секущей. При в силу непрерывности функции расстояние между точками и

стремится к нулю. Точка по кривой приближается к точке , а секущая поворачивается вокруг точки . Ее предельное положение называют касательной к кривой, то есть к графику функции в точке . Тогда из (2) получим угловой коэффициент касательной

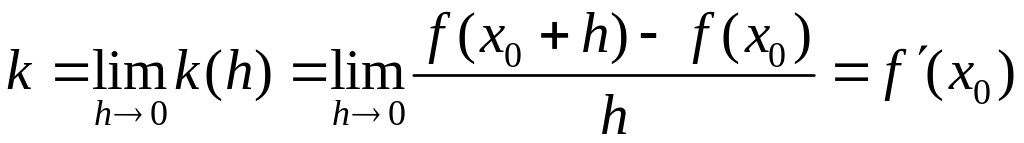. (3)

А из уравнения секущей получим уравнение касательной

. (4)

Из рисунка видно, что угловой коэффициент секущей (2) равен тангенсу угла ее наклона к оси , то есть Так как , то отсюда ясен геометрический смысл производной – это угловой коэффициент касательной в точке . Если или то касательная будет перпендикулярна оси . Ее называют вертикальной касательной, а точку на кривой – точкой перегиба. Говорят, что функция имеет в точке бесконечную производную (см. рис.).

Если левая и правая производные в точке бесконечности разных знаков ( или наоборот), то и в этом случае прямую называют вертикальной касательной, а точку на кривой называют точкой возврата графика функции (см. рис.).

Пример 1. Найти касательную к графику функции в точке (см. рис.).

Решение.

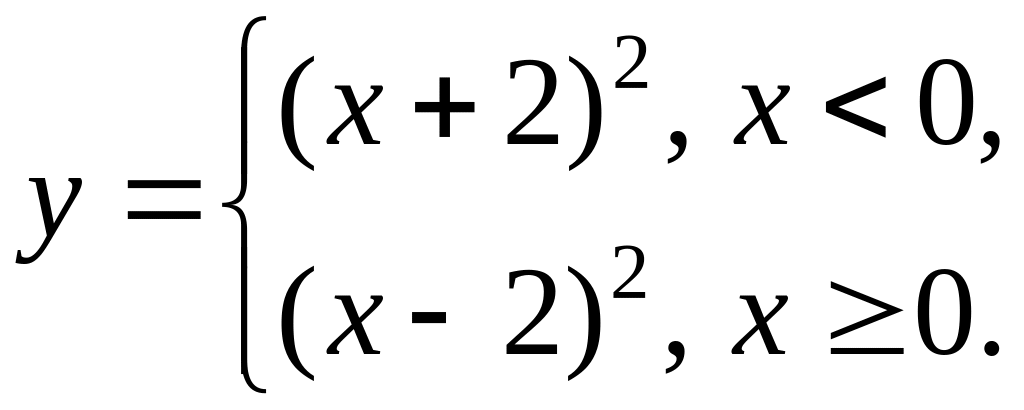
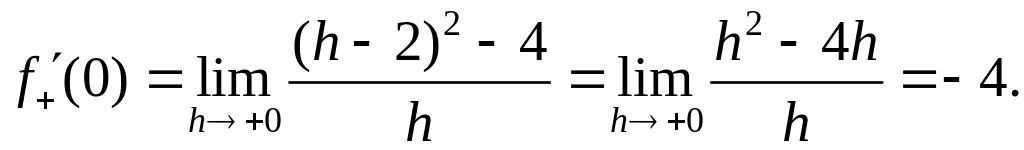
Так как функция не имеет производной в точке , то не имеет и касательной в точке . Однако, есть левая и правая касательные в этой точке: и . Точка графика функции называется угловой.

Пример 2. Найти касательную к графику функции в точке .

Решение.   – вертикальная касательная (см. рис. 5.7).

Пример 3. Найти производную в точке .

Решение.

, .

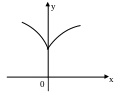
Функция не имеет бесконечной производной в точке , но имеет вертикальную касательную. Точка (0,1) графика функции является точкой возврата (см. рис.).

Пусть – закон движения точки по траектории, то есть закон изменения пути от времени .

Пусть в момент времени точка находится в пункте , а в момент времени в пункте , то есть за время точка прошла путь, равный

(см. рис.).

Величину

называют средней скоростью движения точки на участке , а

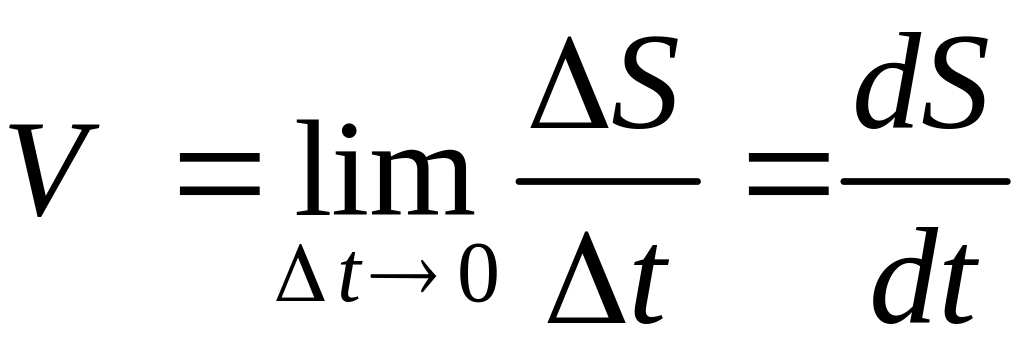
называют величиной мгновенной скорости в момент времени . Таким образом, одна из физических интерпретаций производной – скорость движения точки.

Пусть  – масса стержня длиной . Тогда  – масса стержня длиной , а средняя плотность участка стержня длиной . 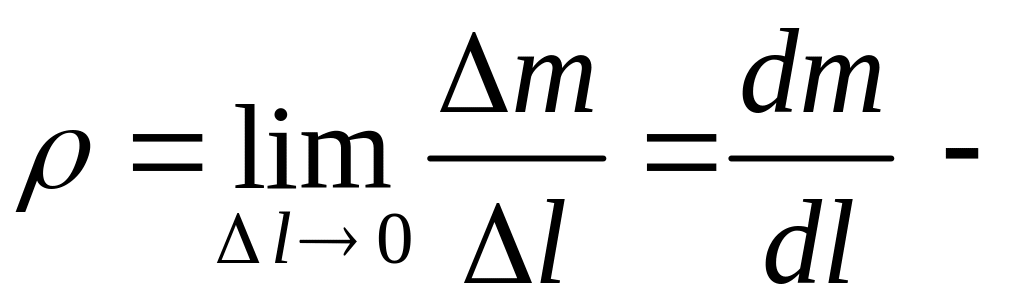линейная (погонная) плотность стержня.

Пусть  – количество электричества, протекающее через поперечное сечение проводника за время . Тогда количество электричества, протекающее за время ,  средний ток за время , а мгновенный ток в момент времени .

Можно привести и другие интерпретации производной.