50.Преобразование графиков функций.

51.Предел числовой последовательности. Основные теоремы о пределах.

Постоянная «А» называется пределом переменной , если разность между ними есть б.м.в., т.е.

Определение: Постоянная А называется пределом числовой пос-ти , если для любого сколь угодно малого положительного числа Ɛ найдется такой номер N, зависящий от Ɛ, что при всех значениях n>N справедливо неравенство . Число A-предел, -любое число.

>N) выполняется неравенство

Теоремы.

1)

2)

3)

4)

Сл.1

Сл.2

52.Предел функции в точке и на бесконечности.

А называется f(x) в точке если для любой пос-ти соответствует значений функций .

y= ,

Постоянная А называется пределом f(x) в точке , если для любого сколь угодно малого числа Ɛ>0 существует такое число σ>0, что при выполнении равенства |x- |< σ выполняется |f(x)-A|<Ɛ.

А называется при x->+∞, если для любой положительной б.б.пос-ти. , пос-ть соответствующих значений функций сходится к числу А

Определение: А называется пределом функции f(x) при х->+∞, если для любого числа Ɛ>0, найдется такое число M>0, что при всех значениях x>M выполняется неравенство

|f(x)-A|<Ɛ.

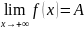
53.Сравнение бесконечно малых величин.

1)Если , то -называется б.м.в. более высокого порядка малости, чем 𝛃.

2)Если , то -называется б.м.в. более низкого порядка малости, чем 𝛃.

3)Если , то 𝛂 и 𝛃 – б.м.в данного порядка малости.

4) Если – называются эквивалентами б.м.в. .

59. Механический смысл производной.

Пусть материальная точка движется прямолинейно по закону S=f(t), предположим, что к моменту точка прошла путь , а к моменту времени t путь s, тогда за промежуток времени △t=t- материальная точка прошла путь △s=s- .

V( )= Мех.смысл.пр-й: скорость прямолинейного движения материальной точки в данный момент времени есть производная от пути по времен, вычисленная в данный момент времени.

54. Замечательные пределы.

Первый замечательный предел.

Первый замечательный предел позволяет открывать неопределенность ( ).

Второй замечательный предел.

позволяет открыть неопределенность

55. Непрерывность функции. Классификация точек разрыва.

Функция f(x) называется непрерывной в точке , если выполняются следующие условия:

1)Функция определена в точке , т.е. существует f( )

2)Существует конечный предел функции при x-> , т.е.

3)Этот предел равен значению функции в точке , т.е.

Функция называется непрерывной в точке б.м.в. приращению аргумента х этой точке соответствует бесконечно-малое п-риращение функции.

△x=x- – приращение аргумента

△y=y- – приращение функции

Классификация точек разрыва:

1)Точки разрыва первого рода (точки, в которых пределы слева и справа конечны, но друг другу не равны)

2)Точки разрыва второго рода. Точки, в которых хотя бы один из пределов слева или справа, равен бесконечности или не существует.

3)Точки устранимого режима – это точки, в разрыве которых предел функции существует(но не равен значению функции в этой точке).

К точкам устранимого разрыва относят к точкам разрыва первого рода.