43.Эллипс. Каноническое уравнение эллипса. Исследование формы эллипса по его каноническому уравнению.

1)Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух заданных точек F1 и F2 , называемых фокусами эллипса, есть величина постоянная.

=2a – большая ось, a – большая полуось. -маленькая оси эллипса,b-малая полуось.

| |+| |=2a=const, 2a>2c, |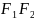 |=2C – фокусное расстояние. -фокусы эллипса.

2) параметры эллипса–

Каноническое уравнение эллипса.

3)a>b, 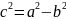. b>a,

Первый вариант, как на рисунке, второй – вдоль оси Y.(оси не меняются)

44.Эксцентриситет эллипса. Связь эллипса с окружностью.

Эксцентриситет эллипса – это отношение расстояние между фокусами к длине большой оси.

1)a>b, Ɛ=

2)b>a, Ɛ=

0< Ɛ<1. a=b.

=1

45. Гипербола. Каноническое уравнение гиперболы. Исследование формы гиперболы по её уравнению.

где r и d не писать, линии, которые проходят через о;о – асимптоты.

Пусть на плоскости заданы две точки и и дано число a (0 < a < c). Гипербола - множество точек M плоскости, для каждой из которых модуль разности расстояний от точек и равен 2a. Точки и называются фокусами гиперболы; - действительная ось; - мнимая ось; O - центр; - левый и правый фокусы; - вершины.

–каноническое уравнение гиперболы.

Равнобочная гипербола (как на рисунке)

Сопряженная гипербола (ветви сверху и снизу)

46.Эксцентриситет гиперболы. Равносторонняя гипербола.

Эксцентриситетом гиперболы называется отношение расстояние между фокусами к длине действительной оси.

Ɛ= , Ɛ>1

Равносторонняя гипербола. a=b.

=> – уравнение равносторонней гиперболы. 0 (0;0) – центр гиперболы.

48. Понятие функции. Классификация функций.

Ф ункция — зависимость между двумя или большим количеством величин, при которой каждым значениям одних величин, называемых аргументами функции, ставятся в соответствие значения других величин, называемых значениями функции.

Элементарные функции делятся на два класса.

1 класс алгебраических функций:

а) у = А0хп + А1хп-1 + А2 – многочлен

б) у = ( А0хп + А1хп-1 + . + Ап)/(В0хм + В1хм-1 + . +Вм) – дробно-рациональная

2 класс трансценденных функций.

а) у = ах, а > 0, а ≠1, показательная функция,

б) у = logах, а> 0, а ≠1, логарифмическая функция,

в) все тригонометрические функции,

г) все обратные тригонометрические функции,

д) функции вида у = хL , где L – иррациональное число.

47.Парабола. Каноническое уравнение параболы. Исследование формы параболы по её уравнению.

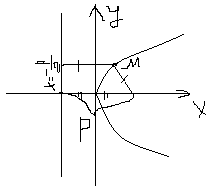
x – прямая, которая называется директриса

- каноническое уравнение параболы.

p>0, p – расстояние от фокуса до директрисы.

F( ;0)-фокус, О(0;0)-вершина

, F(- ;0)

49. Бесконечно малые величины и их свойства. Бесконечно большие величины.

Б.м.в обратна по величине б.б.в.. Свойства бесконечно малых:

1)Сумма конечного числа бесконечно малых — бесконечно малая.

2)Произведение бесконечно малых — бесконечно малая.

3)Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

4)Если — бесконечно малая последовательность, сохраняющая знак, то бесконечно большая последовательность.

Б.б.в- это такая переменная, которая по абсолютной величине неограниченно-возрастает.