§4. Неоднорідні системи лінійних алгебраїчних рівнянь.

1. Зв’язок між розв’язками неоднорідної та зведеної однорідної систем лінійних рівнянь. Розглянемо сумісну неоднорідну систему лінійних алгебраїчних рівнянь

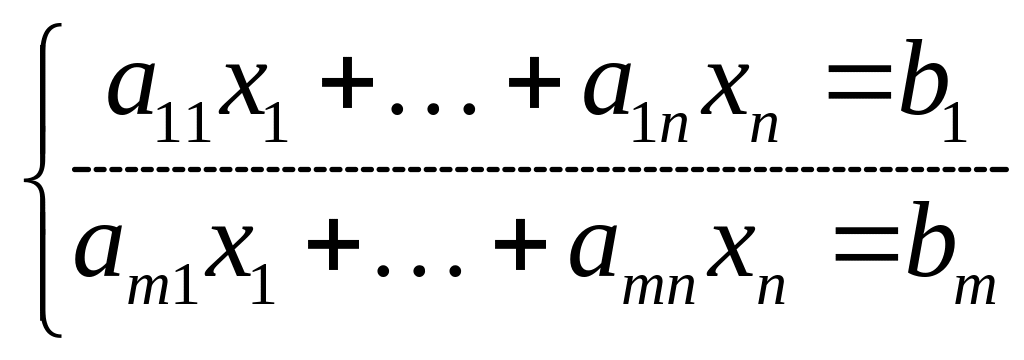. (14)

Системі (14) можна однозначно співставити однорідну систему

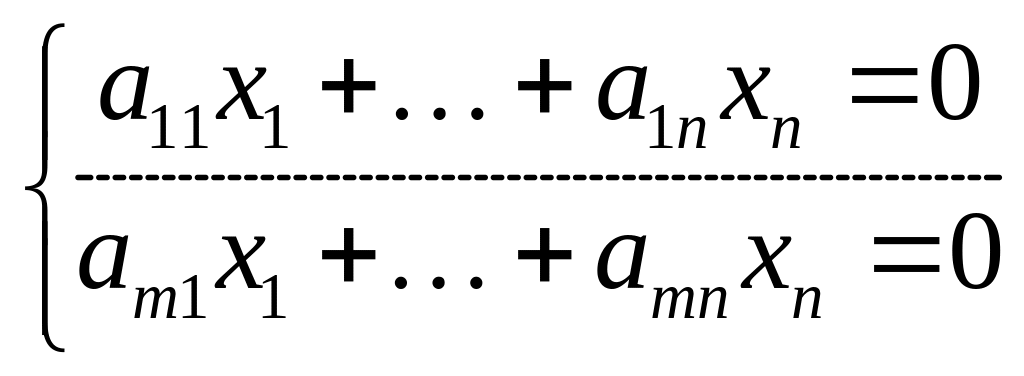, (15)

яка називається зведеною.

Запишемо системи (14), (15) в матричній формі:

,

,

де , , .

Теорема 1. Сума будь-якого розв’язку неоднорідної системи та будь-якого розв’язку зведеної однорідної системи є розв’язком неоднорідної системи.

Доведення. Нехай – який-небудь розв’язок неоднорідної системи , а – розв’язок відповідної зведеної однорідної системи . Підставимо суму в ліву частину системи :

,

тобто є розв’язком системи (14).

Теорема 2. Різниця будь-яких двох розв’язків неоднорідної системи є розв’язком зведеної однорідної системи.

Доведення. Нехай , – два довільні розв’язки неоднорідної системи (14). Підставимо різницю в ліву частину системи :

.

Теорему доведено.

2. Лінійний многовид розв’язків неоднорідної системи. Нехай – який-небудь розв’язок неоднорідної системи (14), а – довільний розв’язок зведеної однорідної системи (15) і розглянемо вектор

. (16)

Зафіксуємо вектор , а вектор будемо змінювати так, щоб він пробігав увесь лінійний підпростір розв’язків зведеної однорідної системи (15). За теоремою 1, кожний отриманий таким способом вектор є розв’язком неоднорідної системи (14). Покажемо, що формула (16) вичерпує всі можливі розв’язки неоднорідної системи (14). Справді, нехай – який-небудь розв’язок системи (14). За теоремою 2, вектор є розв’язком зведеної однорідної системи. Позначимо вектор через , . Тоді , тобто кожний розв’язок неоднорідної системи отримується за формулою (16).

Деталізуємо рівність (16). Нехай ранг зведеної однорідної системи (15) дорівнює і нехай фундаментальна система розв’язків цієї системи складається з лінійно незалежних векторів . Тоді рівність (16) можна переписати у такому вигляді:

. (17)

Рівність (17) задає всі розв’язки неоднорідної системи (14) – кожний розв’язок отримується при певних значеннях числових параметрів . Рівність (17) називається загальним розв’язком неоднорідної системи (14), а її окремий, хоч і довільний розв’язок називається частинним розв’язком. Таким чином, загальний розв’язок лінійної неоднорідної системи є сумою загального розв’язку зведеної однорідної системи та якого-небудь частинного розв’язку заданої неоднорідної системи.

Лінійна оболонка є –вимірним лінійним підпростором розв’язків зведеної однорідної системи, тобто -площиною, що проходить через початок координат. Сума визначає –площину, яка отримується паралельним зсувом підпростору розв’язків на вектор . Саме ця –площина і називається лінійним многовидом розв’язків неоднорідної системи (14).

Приклад. Знайти загальний розв’язок системи лінійних алгебраїчних рівнянь

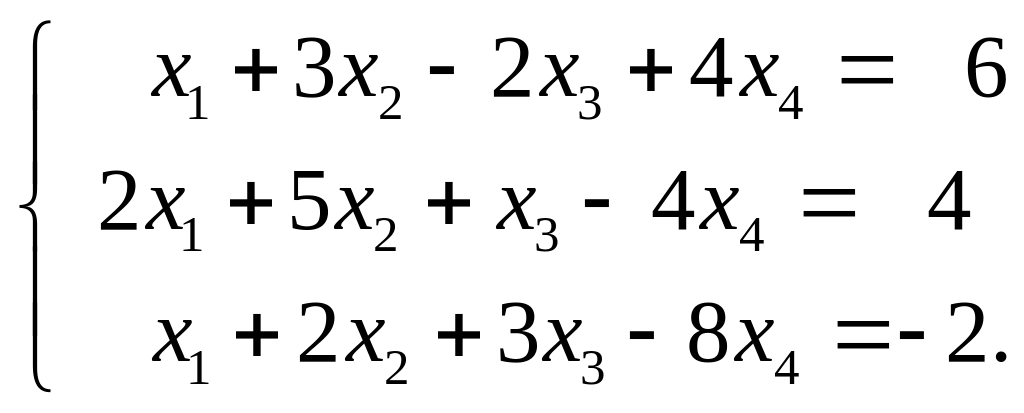
Випишемо розширену матрицю заданої системи

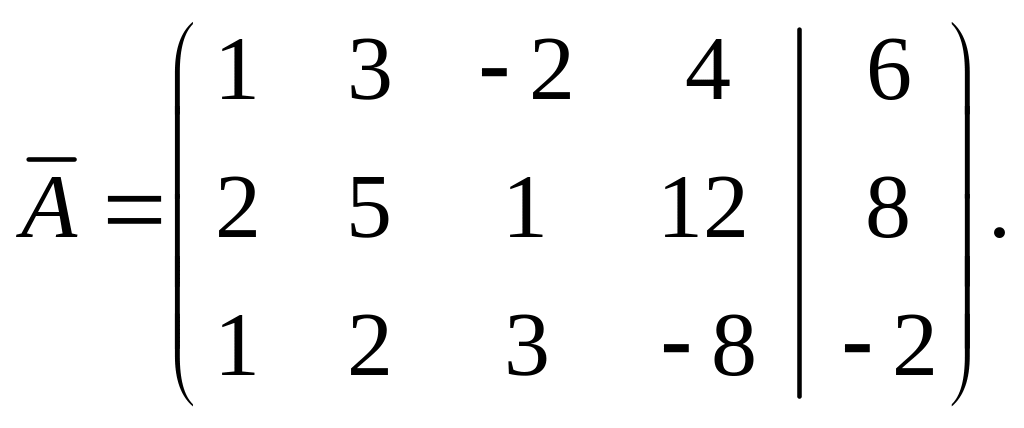
Шляхом елементарних перетворень матриці отримуємо матрицю

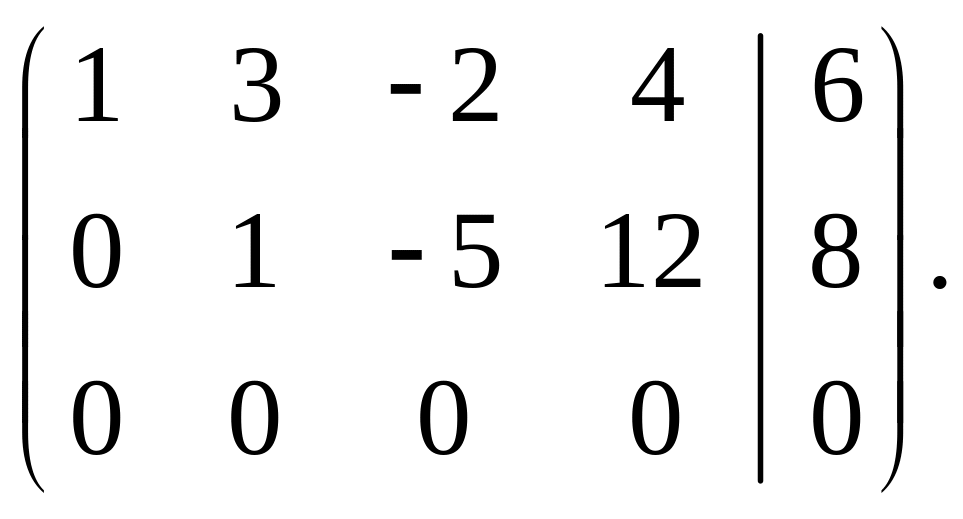
Звідси , тобто система сумісна, до того ж базисний мінор

утворюється коефіцієнтами перших двох рівнянь, а третє рівняння є їх лінійною комбінацією. Таким чином, максимальна лінійно незалежна підсистема виглядає так:

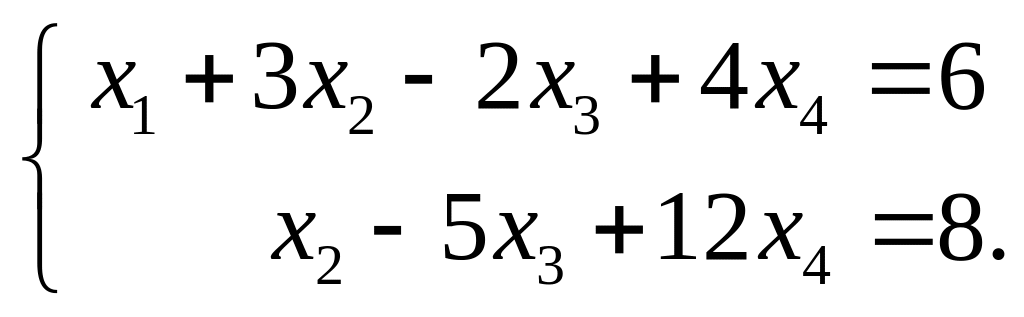
Базисні невідомі залишимо зліва, а вільні невідомі перенесемо направо

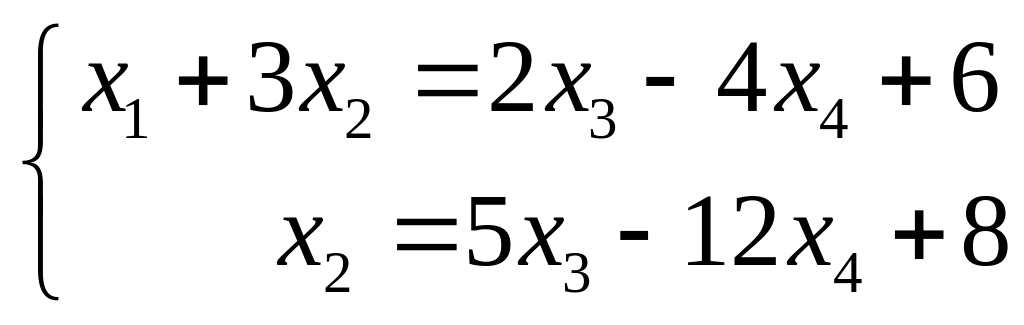
і розв’яжемо отриману систему методом Гауса:

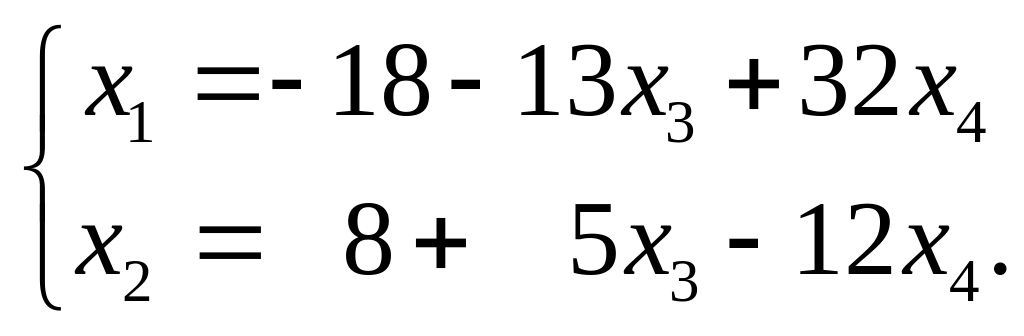
Долучимо до отриманих рівностей ще дві очевидні рівності:

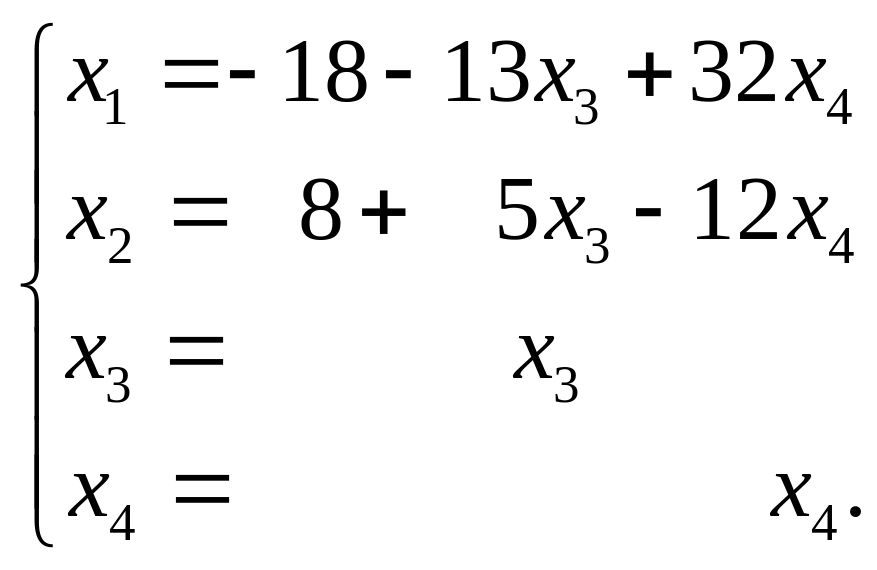
Позначивши вільні невідомі через відповідно, перепишемо цю систему рівностей у матричній формі:

.

Будемо розглядати матриці-стовпчики як вектори. Позначимо , , , . Тоді отриману рівність можна переписати у векторній формі

Це і є загальний розв’язок заданої системи. Пара векторів утворює фундаментальну систему розв’язків, а є загальним розв’язком зведеної однорідної системи; вектор є частинним розв’язком заданої системи.

3. Метод найменших квадратів. Нагадаємо, що згідно з теоремою Кронекера-Капеллі, система (2) сумісна тоді і лише тоді, коли . Нехай . Тоді . Звідси, якщо , то така система, як правило, несумісна. З цієї причини, на перший погляд, нема жодного сенсу розглядати системи, в яких число рівнянь перевищує число невідомих. Однак це не так, бо існують задачі, які вимагають розгляду таких систем. Наведемо приклад. Припустимо, що деяка величина лінійно залежить від величин , , але значення постійних коефіцієнтів цієї залежності невідомі. Припустимо додатково, що значення величин можна виміряти, провівши відповідний експеримент. Проведемо серію з експериментів і позначимо результати вимірювання у –тому експерименті через . Тепер можна спробувати знайти невідомі коефіцієнти як розв’язок системи

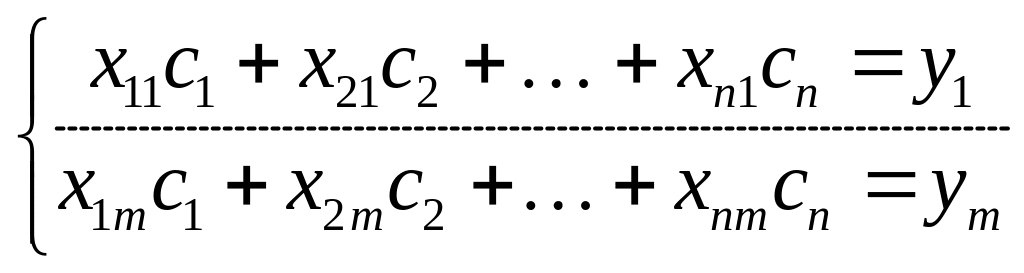. (18)

Відповідні теореми теорії ймовірностей гарантують, що кінцевий результат вимірювань буде тим точнішим, чим більше буде проведено незалежних вимірювань. Тому, як правило, система (18) має більше рівнянь, ніж невідомих.

Розглянемо систему

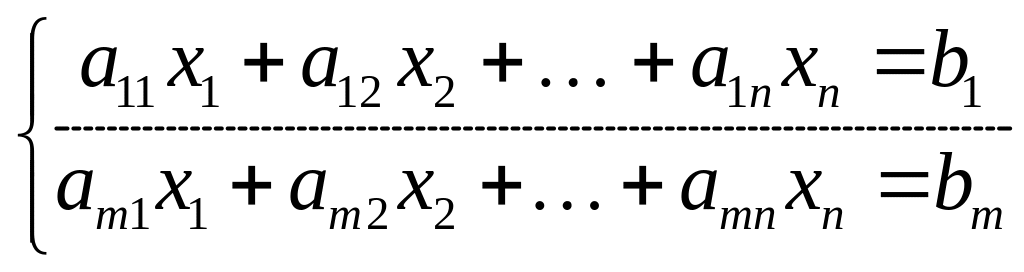, (19)

для якої . Оскільки система (19) несумісна, то для неї можна знайти лише наближений розв’язок – такі значення невідомих, при яких ліві частини системи (19) якнайменше відрізняються від правих частин. Для більш точної постановки задачі перепишемо систему (19) у такому вигляді:

.

Позначимо , , , , і будемо вважати, що вектори є векторами –вимірного евклідового простору зі скалярним добутком , , . Тоді ліві частини системи (19) є компонентами вектора . Позначимо . Тоді . Звідси зрозуміло, що вектор буде найменше відрізнятися від вектора лише у тому випадку, коли довжина вектора буде мінімальною, а це можливо лише тоді, коли є ортогональною проекцією вектора на підпростір . Таким чином, для наближеного розв’язання системи (19) потрібно знайти такі значення невідомих , при яких вектор є ортогональною проекцією вектора на підпростір . З попереднього розділу відомо, що ортогональна проекція вектора на підпростір знаходиться зі системи

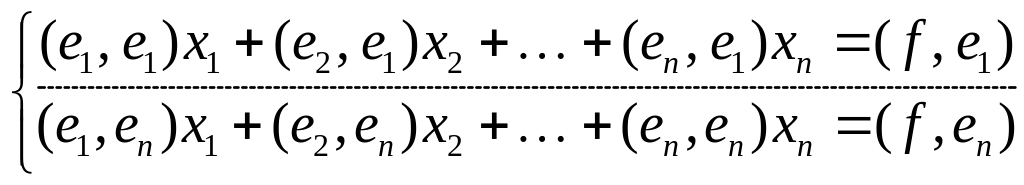. (20)

Система (20) називається системою нормальних рівнянь. Таким чином, знаходження наближеного розв’язку системи (19) зводиться до розв’язування нормальної системи (20) рівнянь з невідомими.

Підсумовуючи, можна сказати, що запропонований спосіб розв’язування системи (19) зводиться до мінімізації величини

,

яка називається середньоквадратичним відхиленням і зовнішній вигляд якої спричинився до назви методу.

Приклад. Розв’язати методом найменших квадратів систему рівнянь

.

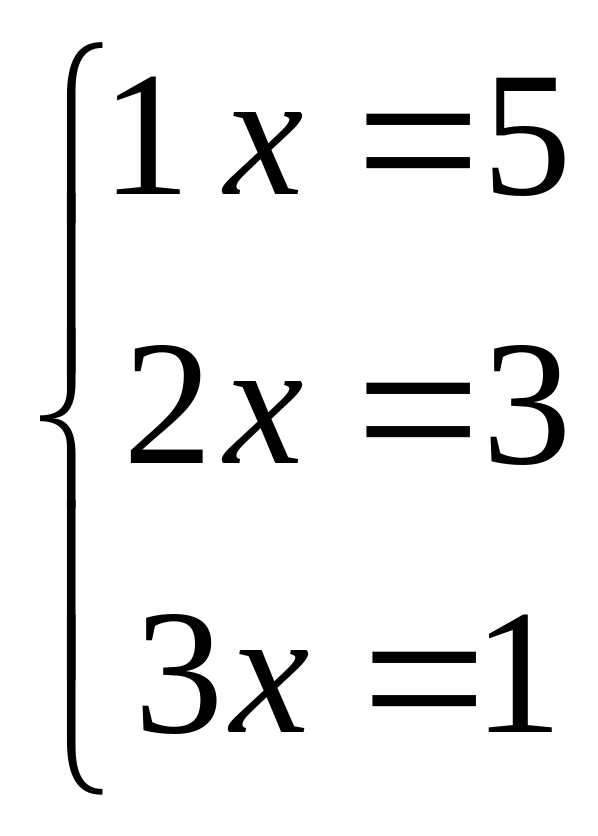Згідно з нашими позначеннями, , . Нормальна система складається з одного рівняння

,

тобто , звідки .