16. Собственно-случайная выборка – оценки, ошибки.

Выборка называется собственно случайной, если при извлечении выборки объема все возможные комбинации из элементов, которые могут быть получены из генеральной совокупности объема, имеют равную вероятность быть извлеченными.

Собственно случайная выборка формируется в строгом соответствии с научными принципами и правилами случайного отбора. Для получения собственно случайной выборки генеральная совокупность строго подразделяется на единицы отбора, и затем в случайном повторном или бесповторном порядке отбирается достаточное число единиц. Случайный порядок – это порядок, равносильный жеребьевке. На практике такой порядок лучшим образом обеспечивается при использовании специальных таблиц случайных чисел.

При бесповторном способе отбора расчет стандартной ошибки осуществляется с помощью формулы:

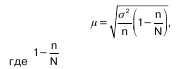
 —доля единиц генеральной совокупности, не попавших в выборку.

Формировать выборку в строгом соответствии с правилами случайного отбора практически очень сложно, а иногда невозможно, так как при использовании таблиц случайных чисел необходимо пронумеровать все единицы генеральной совокупности.

20. Равномерное распределение.

Равномерное распределение, прямоугольное распределение, специальный вид распределения вероятностей случайной величины Х, принимающей значения из интервала (а — h, a + h); характеризуется плотностью вероятности:

.

  Математическое ожидание:

Ех = a, дисперсия Dx = h²/3, характеристическая функция:  .

  С помощью линейного преобразования интервал (а — h, a + h) может быть переведён в любой заданный интервал. Так, величина Y = (X — a + h)/2h равномерно распределена на интервале (0, 1). Если Y₁, Y₂, ...,Y_n равномерно распределены на интервале (0, 1), то закон распределения их сумм ы, нормированной математическим ожиданием n/2 и дисперсией n/12, при возрастании n быстро приближается к нормальному распределению (даже при n = 3 приближение часто бывает достаточным для практики).

21. Нормальное распределение.

Любая случайная величина имеет функцию распределения - зависимость плотности вероятности от значения случайной величины. Для нормального распределения (распределения Гаусса) функция распределения имеет следующий вид:

 

 - матожидание (генеральное среднее)  - стандартное отклонение

Для проведения статистических расчетов часто необходимо располагать информацией о виде функции распределения.

22. Распределение Стьюдента.

Распределение Стьюдента по сути представляет собой сумму нескольких нормально распределенных случайных величин. Чем больше величин, тем больше верятность, что их сумма будет иметь нормальное распределение. Таким образом, количество суммруемых величин определяет важнейший параметр формы данного распредения - число степеней свободы

РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА — распределение, заданное функцией плотности: , -∞ < x < ∞; параметр n называется числом степеней свободы, Γ (υ) — гамма-функция. Если X, X1, X2, …, Хп — независимые случайные величины, распределенные по нормальному закону (см. Распределение нормальное ) с параметрами (0, σ), то случайная величина распределена по закону Стьюдента. Дисперсия . Все моменты нечетного порядка равны нулю, а при 2ν < n центр. моменты равны начальным: . Для больших n величина t асимптотически нормальна с параметрами (0, 1). В геологии Р. С. используется для сравнения выборочных средних двух выборок, если осуществляются условия его применимости. В частности, на основе Р. С. могут быть уточнены представления о кондиционности руд или перспективности рудоносных площадей.