
- •1. Предмет технической термодинамики и ее задачи
- •2Основные параметры состояния газа
- •3. Законы идеальных газов. Уравнение состояния идеального газа
- •4. Газовые смеси
- •5. Эквивалентность теплоты и работы
- •6 Термодинам. Проц.
- •7 Внутренняя энергии газа
- •8 Работа Расширения
- •9 Определения. Истинная и средняя теплоемкость
- •10 Изобарная и изохорная теплоемкость идеального газа
- •11 Зависимость теплоемкости газов от температуры
- •12 Теплоёмкость смеси газов
- •13 Основные термодинамические процессы.
12 Теплоёмкость смеси газов
При задании смеси массовыми долями массовая теплоёмкость смеси определяется по формуле: с=g1c1+g2c2+..+gncn
g1c1, g2c2 –произведения массовой доли на массовую теплоёмкость каждого газа из состава смеси в данном процессе.
При задании
смеси объёмными долями объёмная
теплоёмкость смеси может быть найдена
по формуле: c'=r1c’1+r2c’2+..+rnc’n
где r1c’1,
r2c’2-произведения
объёмной доли на объёмную теплоёмкость
каждого газа из состава смеси в данном
процессе. Массовая теплоёмкость cv=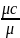 cp=cv+R
кДж/кгК
cp=cv+R
кДж/кгК
22.4 –объём
одного киломоля газа при н.у. R-газовая
постоянная, работа в изоб. Процессе
измер. В Дж при изменении t на 1о
Объёмная теплоёмкость определяется
по формулам: c’=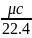 c’p=c’v+R
кДж/м3К . Средняя объёмная
теплоёмкость
c’p=c’v+R
кДж/м3К . Средняя объёмная
теплоёмкость
с'pm=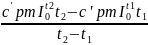 с'pm- по таблице П3
с'pm- по таблице П3
13 Основные термодинамические процессы.
Изменение
состояния газа характеризуется
изменением всех его основных параметров
p,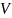 ,t.
При этом теплота подводиться или
отводится- политропные процессы.
Остальные процессы в которых какой
либо из основных параметров не меняется
или процесс осуществляется без
теплообмена с внешней средой. Их 4:
изохорный(
=const)
изобарный(p=const)
изотермический(t=const)
адиабатный(dq=o).
При изучении процесса определяют 1)
зависимость между изменяющимися
параметрами состояния газа 2) кол-во
теплоты подводимой и изменение его
внутр. Энергии 3) работу, совершаемую
газом при расширении. Первый закон
термодинамики используется при
исследовании- переход энергии происходит
по закону эквивалентности, тоесть
опред. Кол-ву энергии данного вида
всегда соответствует одно и тоже кол-во
энергии др. вида.
,t.
При этом теплота подводиться или
отводится- политропные процессы.
Остальные процессы в которых какой
либо из основных параметров не меняется
или процесс осуществляется без
теплообмена с внешней средой. Их 4:
изохорный(
=const)
изобарный(p=const)
изотермический(t=const)
адиабатный(dq=o).
При изучении процесса определяют 1)
зависимость между изменяющимися
параметрами состояния газа 2) кол-во
теплоты подводимой и изменение его
внутр. Энергии 3) работу, совершаемую
газом при расширении. Первый закон
термодинамики используется при
исследовании- переход энергии происходит
по закону эквивалентности, тоесть
опред. Кол-ву энергии данного вида
всегда соответствует одно и тоже кол-во
энергии др. вида.
Q=AL, L=EQ L-работа перешедшая в теплоту (кгсм) Q-теплота полученная за счёт работы (ккал) A-коэф. Пропорциональности(термич. Эквивалент работы) E- мех. Эквивалент теплоты. Е=427 кгсм/ккал. А=1/Е ккал/кгсм
14 ИЗОТЕРМИ́ЧЕСКИЙ ПРОЦЕ́СС -термодинамический процесс, протекающий в системе при постоянной температуре T=const. На термодинамической диаграмме (графическое изображение процесса) изображается изотермой. Диаграмма изотермического процесса (изотерма) в координатах давление p — объем V изображается гиперболой (pV=const).
PV = RT =const, PV=const P1/P2=V1/V2 – давление измен. Обратно пропорц. объёму.
Изменения внутренней энергии и энтальпии зависят только от температуры.
∆u=Cv(t2-t1)=0 u=const ∆i=Cp(t2-t1)=0 i=const по первому закону термодинамики g=l Т.к. PV=P1V1 ; P= P1V1/V, то
ℓ=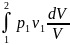 =
=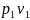 ln
ln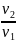 =RT
ln
С=dg/dt=
=RT
ln
С=dg/dt=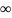 ;
;
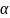 =∆u/g=0
=∆u/g=0
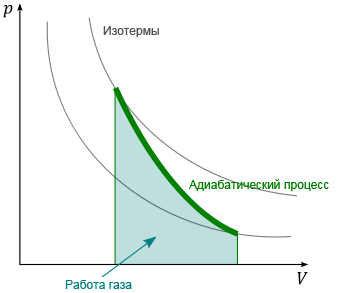
15 Адиабатный процесс – процесс который осуществляется без теплообмена между газом и внешней средой.
dq=0 ; du+pdV=0; Cvdt=pdv=0. Работа процесса dq=0, работа совершается за счёт внутр. Энергии. ℓ=-∆u=Cv(t1-t2)
q=∆u+
ℓ; ℓ=R/k-1
(t1-t2)
т.к. P1V1 = RT
и P2V2=RT2,
работа будет равна ℓ=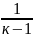 (P1V1-
P2V2)=
ℓ=
(P1V1-
P2V2)=
ℓ=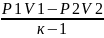
С=dg/dt=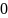 ;
=∆u/g=
;
=∆u/g=
16 Политропные процессы- всякий обратимый термодинамический процесс, который подчиняется уравнению PVn=const
n(-
;
)
При n=0 изобарный, При n=1
изотермический, При n=к
адиабатный P1/P2=(U2/U1)n
и (U2/U1)=
(P1/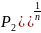
T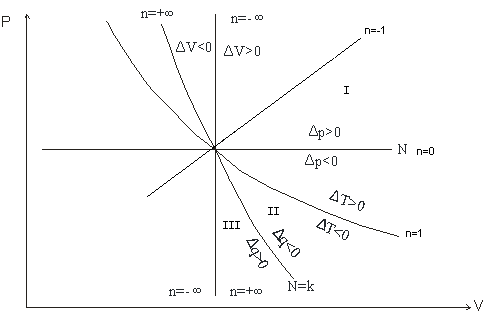 2/T1=(P2/
2/T1=(P2/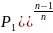 T2/T1=(U1/U2)n-1
T2/T1=(U1/U2)n-1
ℓ=R/n-1 (t1-t2) ℓ=1/n-1(P1V1- P2V2).
Теплоёмкость
для политропного процесса ∆q=∆u+ℓ
; ∆u=Cv∆t;
q=Cv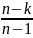 (t2-t1)
(t2-t1)
α=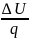 =
=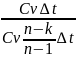 =
=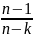
1гр
α=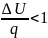 ; dq
; dq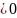 ;
;
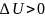 ;
dt
;
dt 0
0
2гр
1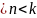 ; α=
«-»
; α=
«-»
3гр
k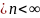 ; α
; α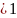
1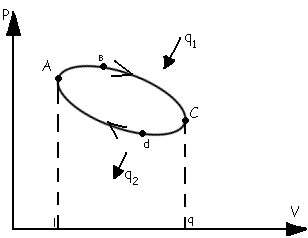 7
Круговые процессы-
процессы в которых рабочее тело пройдя
ряд различных состояний возвращается
в исходное состояние. ℓ1=пл.
eaвcf ℓ2=пл. eadcf
ℓ1
ℓ2
7
Круговые процессы-
процессы в которых рабочее тело пройдя
ряд различных состояний возвращается
в исходное состояние. ℓ1=пл.
eaвcf ℓ2=пл. eadcf
ℓ1
ℓ2
ℓц=
ℓ1- ℓ2=пл. aвcda
; qц=q1-q2
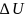 =0
qц= ℓц qц-
полезно использованная теплота за цикл
=0
qц= ℓц qц-
полезно использованная теплота за цикл
ℓц-полезная
работа цикла. Термический КПД
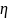 =
=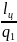 =
=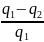 =1-
=1-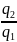 Так как в прямых
Так как в прямых
циклах q1 всегда больше q2, то кпд всегда меньше единицы. Если процессы входящие в цикл равновесные и обратимые то цикл обратимый. Если какой либо процесс входящий в цикл неравновесный, то и весь цикл будет неравновесным, необратимым.
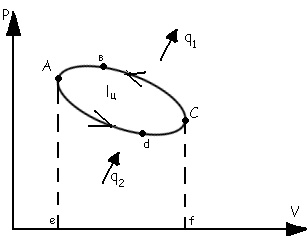
Обратный круговой цикл. ℓ1=пл. eaвcf-процесс сжатия ℓ2=пл. eadcf-процесс расширения
ℓ1 ℓ2 ℓц= ℓ2- ℓ1=пл. aвcd-отриц.; -qц= q2 - q1 ; q1= q2+ ℓц ; -qц= -ℓц ; -ℓц = q2 - q1
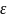 =
=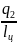 - холодильный коэффициент. Таким
образом, горячим источникам передаётся
теплота холодильника и теплота,
эквивалентная работе цикла.
- холодильный коэффициент. Таким
образом, горячим источникам передаётся
теплота холодильника и теплота,
эквивалентная работе цикла.
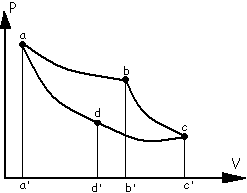
18 Прямой обратимый цикл Карно. Является идеальным циклом, состоит из двух изотермических и двух адибатных процессов. В цикле испол. 1 кг идеального газа.
Движение идёт а-b-c- d-a. Газ расширяется по изотерме ab при Т1 получая теплоту q1 которая полностью переходит в работу. q1= ℓ1 =RT1ln(Vb/Va)=пл. a’abb’. Газ расширяется по адиабате bc, совершая работу за счёт внутр энергии, темпер. понижается до T2. ℓbc=-∆Ubc=Cv(T1-T2)=пл. b’bcc’.
q=∆U+ℓ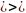 ∆U=-ℓ. dq=0.
По изотерме cd газ сжимается при постоян.
T2. q2=ℓ2=-RT2ln(Vc/Vd)=пл.d’ddc’.
По адиабате da газ сжимается и возвращается
в нач. состояние.
∆U=-ℓ. dq=0.
По изотерме cd газ сжимается при постоян.
T2. q2=ℓ2=-RT2ln(Vc/Vd)=пл.d’ddc’.
По адиабате da газ сжимается и возвращается
в нач. состояние.
ℓda=-∆Uda=-Cv(T1-T2)=пл.a’add’.
Работа газа за цикл будет равна разности
работ, которую он совершает при
изотермическом сжатии и расширении.
Термический КПД зависит только от
температуры горячего источника Т1
и температуры холодильника Т2.
=1-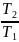 =
=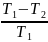 .
Чем выше температура горячего источника
и чем ниже температура холодильника,
тем выше терм. кпд. КПД цикла Карно
всегда меньше 1( значит что теплоту q1
подводимую к рабочему тело невозможно
полностью превратить в работу, часть
её в кол-во q2 отдаётся
холод. источнику. КПД не зависит от
природы рабочего тела.
.
Чем выше температура горячего источника
и чем ниже температура холодильника,
тем выше терм. кпд. КПД цикла Карно
всегда меньше 1( значит что теплоту q1
подводимую к рабочему тело невозможно
полностью превратить в работу, часть
её в кол-во q2 отдаётся
холод. источнику. КПД не зависит от
природы рабочего тела.
1
9
Обратный обратимый цикл Карно.
Движение идёт a-d-c-b-a.
Сначала происходит адиабатное расширение
ad температура понижается от Т1
до Т2. Следующее расширение по
изотерме dc газ получает теплоту от
холодильника в кол-ве q2 при
постоянной Т2. Следующее сжатие
по адиабате cb а затем по изотерме ba газ
возвращается в исходное состояние. При
адиабатном сжатии температура газа
повышается от Т2 до Т1. При
изотермическом сжатии газ отдаёт
горячему источнику теплоту в кол-ве q1
при постоянной Т1. На осуществление
обратного цикла Карно затрачивается
внешняя работа ℓц=пл. abcd. Тепловой
баланс цикла q2-q1=-ℓц.
Таким образом передача теплоты q2
от холодного источника к горячему путем
затраты внешней работы. Холод. коэф. Не
зависит от св-в или природы раб. тела.
С ум. Т2 и ув. Т2 холод. коэф.
увеличивается.
=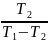
20 Второй закон термодинамики. 1 В круговом процессе подводимая теплота не может быть полностью превращена в работу. 2 Для превращения теплоты в работу необходимо иметь не только нагреватель, но и холодильник с более низкой температурой, т.е. необходим температурный перепад. 3 Теплота не может сама собой переходить от тел с низшей температурой к телам с более высокой температурой.
21 Математической
выражение 2го закона термодинамики.
Энтрапия. .
=1-
=1-
;
=
. Приведённая теплота- отношение теплоты
к абсолютной температуре, при которой
она подводится к телу или от него
отводится. Следовательно для обратимого
цикла Карно алгебраическая сумма
приведённых теплот равна нулю.
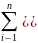 +
+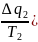 =0
=0
Энтрапия
–это функция зависящая от прост. парам.
характер. состояние термодинам. сист.
и является отношением кол-ва теплоты
подведённой к термод. температуре.
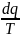 =ds
изменение энтропии системы(горячий
источник, рабочее тело и холодный
источник) в результате прохождения
обратимого цикла равна нулю. ; S=
=ds
изменение энтропии системы(горячий
источник, рабочее тело и холодный
источник) в результате прохождения
обратимого цикла равна нулю. ; S=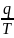 дж/кгк ; dq=du+dl=CvdT+pdV
l:T
дж/кгк ; dq=du+dl=CvdT+pdV
l:T
=ds=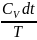 +R
+R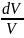
22
T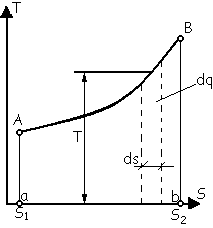 ,s
диграмма. В технической
термодинамике при исследовании процессов
широко применяется T,s
диграмма, на котрой по оси ординат
откладываются значения абсолютных
температур, по оси абсцисс- энтропии.
Как видно из диаграммы, заштрихованная
элементарная площадка с основанием ds
и высотой Т изображает теплоту dq=T ds.
Тогда вся площадь aABb равная сумме
бесконечно большого числа элементарных
площадок будет изобрадать полную
теплоту процесса A-B. Т.е. плaABb=
,s
диграмма. В технической
термодинамике при исследовании процессов
широко применяется T,s
диграмма, на котрой по оси ординат
откладываются значения абсолютных
температур, по оси абсцисс- энтропии.
Как видно из диаграммы, заштрихованная
элементарная площадка с основанием ds
и высотой Т изображает теплоту dq=T ds.
Тогда вся площадь aABb равная сумме
бесконечно большого числа элементарных
площадок будет изобрадать полную
теплоту процесса A-B. Т.е. плaABb=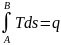 .
В уравнении dq=T ds величина Т всегда
положительна, поэтому dq и ds по знаку
одинаковы. Если в процессе теплота
подводится то dq
,след
и ds
,
энтрапия газа увел. Если в процессе
теплота отводится то dq
0,
ds
0,
энтрапия газа умен. Таким образом
диаграмма позволяет определить кол-во
теплоты, которое подводится к газу или
отводится от него в термодинамическом
процессе и изображается площадкой
под кривой процесса.
.
В уравнении dq=T ds величина Т всегда
положительна, поэтому dq и ds по знаку
одинаковы. Если в процессе теплота
подводится то dq
,след
и ds
,
энтрапия газа увел. Если в процессе
теплота отводится то dq
0,
ds
0,
энтрапия газа умен. Таким образом
диаграмма позволяет определить кол-во
теплоты, которое подводится к газу или
отводится от него в термодинамическом
процессе и изображается площадкой
под кривой процесса.
