
- •1. Предмет технической термодинамики и ее задачи
- •2Основные параметры состояния газа
- •3. Законы идеальных газов. Уравнение состояния идеального газа
- •4. Газовые смеси
- •5. Эквивалентность теплоты и работы
- •6 Термодинам. Проц.
- •7 Внутренняя энергии газа
- •8 Работа Расширения
- •9 Определения. Истинная и средняя теплоемкость
- •10 Изобарная и изохорная теплоемкость идеального газа
- •11 Зависимость теплоемкости газов от температуры
- •12 Теплоёмкость смеси газов
- •13 Основные термодинамические процессы.
7 Внутренняя энергии газа
В технической термодинамике понятие внутренней энергии газа распространяется лишь на ту часть энергии, которая в термодинамических процессах подвергается изменениями Это есть внутренняя кинетическая и внутренняя потенциальная энергии,, сумма их и составляет внутреннюю энергию.
"Внутренняя кинетическая энергия зависит от скорости движения и массы молекул и состоит из энергии поступательного и вращательного движения молекул.а также энергии колебательного движения атомов в самих молекулах Согласно кинетической тео-рии перечисленные виды энергии зависят только от температуры и при ее повышении увеличиваются.
Внутренняя потенциальная : энергия обусловливается силами взаимодействия между молекулами и зависит от растояния между ними и, следовательно, от удельного объема газа который в свою очередь зависит от давления и температуры газа
Таким образом, внутренняя энергия реального газа зависит от основных параметров газа: р, ,T
В
идеальных
газах силы взаимодействия между
молекулами
Отсутствуют и поэтому
внутренняя энергия идеального
газа равна
его внутренней кинетической энергии
и зависит только от
температуры.
Поскольку изменение внутренней энергии
зависит только от начального
и конечного
состояний газа» и не зависит от свойств
процесса, то с математической точки
зрения это означает что дифференциал
внутренней энергии есть полный
дифференциал т.е.
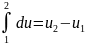
8 Работа Расширения
Работа совершается только при изменении объема газа. Еслипроисходит расширение газа то в этом случае работа совершается против внешних сил, при сжатии газ воспринимает работу внешних сил. При перемещении поршня на бесконечно малое расстояние ds 1кг газа совершит элементарную работу равную
dl=pF ds
pF – полная сила действ на поршень
dl=pd
Так как абсолютное давление р — величина постоянная то dl и dv по знаку одинаковы. Поэтому если dv>O т. е. когда газ расширяется, то и dl>0, следовательно, забота расширения положительна, Если dv<0 т.е. газ сжимается то и dl <0, ■следовательно, работа сжатия отрицательна.
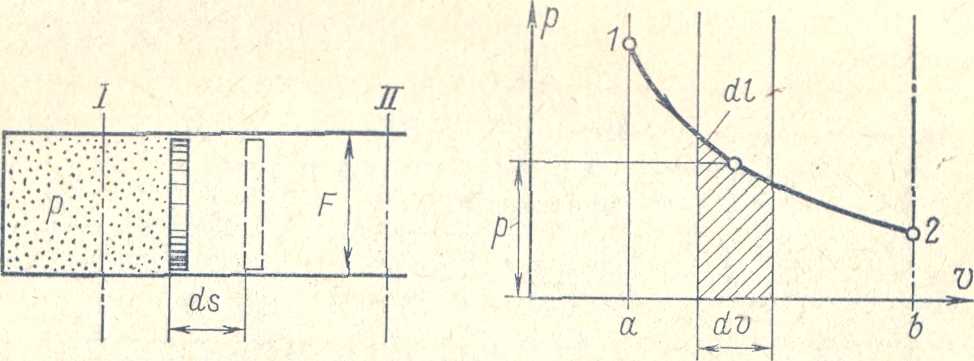
Предположим, что при перемещении поршня из положения 1 в другое крайнее положение 11 удельный^" объем газа ^зменяетгя от значения до значения . Тогда полная работа 1 кг газа будет найдена путем суммирования бесконечно большого числа элементарных работ, т. е. интегрированием в пределах от
До следовательно,
l=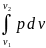
В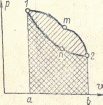 общем случае при изменений
объема
газа
давление его также
изменяется.
общем случае при изменений
объема
газа
давление его также
изменяется.
Таким образом в p, диограмме работа расширения изображается площадью a12b ограниченной кривой процесса осью абсцисс и крайними ординатами.
2-5 Аналитическое выражение первого закона термодинамики. Энтальпия.
Если
в начале процесса
внутренняя
энергия газа равна
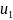 а в конце
а в конце
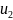 то полное изменение внутренней энеогии
равна
то полное изменение внутренней энеогии
равна
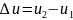
q=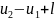
Это уравнение является математическим выражением первого закона термодинамики для конечного процесса. Из уравнения (2-4) следует, что -в общем случае подводимая теплота расходуется на изменение внутренней энергии газа и да совершение внешней работы.
dq=du+pd
В технической термодинамике подводимое к телу тепло считается положительным, отводимое — отрицательным. Изменение внутренней энергии газа счита ется положительным при возрастании температуры газа и отрицательным при ее уменьшении.
Во многих тепловых Расчетах используется величина i называемая энтальпией, которая определяется Из выражения
i=u+p
Отсюда следует, что энтальпия является величиной, определяемой состоянием тела, и, в свою очередь, она определяет состояние тела, т. е. является параметром состояния.
dq=di- dp
dp=di
