21. Сформулируйте теорему об изменении момента количества движения точки.
Количество движения материальной точки - вектор, численно равный произведению массы точки на скорость ее движения и совпадающий с ней по направлению. Моментом количества движения точки относительно некоторого центра О называется векторная величина тоm0 (mv),
определяемая
равенством
где
г — радиус-вектор движущейся точки,
проведенный из центра О.
При
этом вектор m0
(mv) направлен перпендикулярно плоскости,
проходящей через mv и центр О, a
;
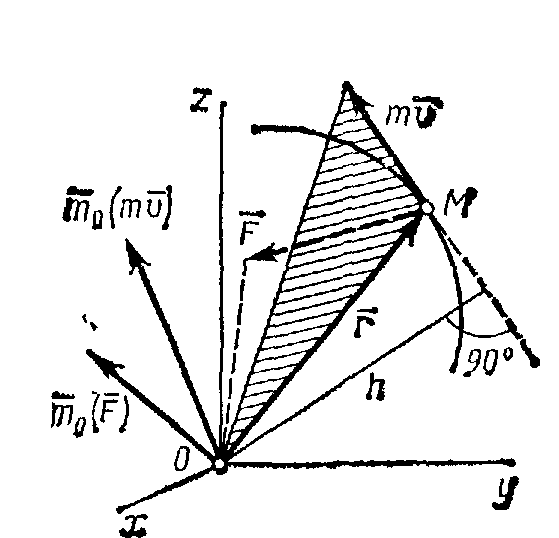для
сравнения на нем показан и вектор
Момент
количества движения точки относительно
какой-нибудь оси Oz, проходящей через
центр О, будет равен проекции вектора
mo(mv) на эту ось:
где
у — угол между вектором m0
(mv) и осью Oz. Теорема моментов устанавливает,
как изменяется со временем вектор
mo(mv). Чтобы доказать ее, продифференцируем
по времени выражение C5). Получим
Ho
как
векторное произведение двух параллельных
векторов, a ma=F, где при действии нескольких
сил
В
результате мы доказали следующую теорему
моментов относительно центра: производная
по времени от момента количества движения
точки, взятого относительно какого-
нибудь неподвижного центра, равна
моменту действующей на точку силы
относительно того же центра. Сравнивая
уравнении, видим, что моменты векторов
mv и F связаны такой же зависимостью,
какой связаны сами векторы mv и F. Если
спроектировать обе части равенства на
какую-нибудь ось Oz, проходящую через
центр О, то, учтя соотношение C6), получим
Это
равенство выражает теорему моментов
относительно оси.
Из уравнения следует, что если mo(F)=0, то mo(mv)=const, т.е. если момент действующей силы относительно некоторого центра равен нулю, то момент количества движения точки относительно этого центра есть величина постоянная. Такой результат имеет место в практически важном случае движения под действием центральной силы. Теорема: векторная производная по времени от момента количества движения материальной точки относительно полюса равна вектору момента силы, действующей на точку относительно того же центра.
Следствия:
1. если линия действия силы проходит через полюс. То момент количества движения относительно этого полюса постоянный;2. если момент силы относительно оси равен нулю, то момент количества движения относительно этой оси постоянный.
20. Сформулируйте теорему об изменении количества движения точки.
Так
как масса точки постоянна, а ее ускорение
a=dv/dt, то уравнение, выражающее основной
закон динамики, можно представить в
виде
Уравнение
выражает одновременно теорему об
изменении количества движения точки в
дифференциальной форме: производная
по времени от количества движения точки
равна сумме действующих на точку сил
*.
Пусть
движущаяся точка имеет в момент времени
t=0
скорость v0, а в момент t1
— скорость v1.
Умножим тогда обе части равенства на
dt
и возьмем от них определенные интегралы.
При этом справа, где интегрирование
идет по времени, пределами интеграла
будут 0 и t1 а слева, где интегрируется
скорость, пределами интеграла будут
соответствующие значения скорости v0 и
v1.
Так как интеграл от d(mv) равен то, то в
результате
Стоящие
справа интегралы, как следует из формулы,
представляют собой импульсы действующих
сил. Поэтому окончательно будет
Уравнение
выражает теорему об изменении количества
движения точки в конечном виде: изменение
количества движения точки за некоторый
промежуток времени равно сумме импульсов
всех действующих на точку сил за тот же
промежуток времени. При решении задач
вместо векторного уравнения часто
пользуются уравнениями в проекциях.
Проектируя обе части равенства
на
координатные' оси, получим