
- •Москва - баку
- •Краткое оглавление
- •Оглавление
- •Предисловие
- •Часть I . Теория управления рынком
- •Глава I. Методологические основы управления
- •1.1 Экономические категории теории управления и менеджмента
- •1.1.1. Понятия и категории организации управления.
- •1.1.2. Элементы и категории менеджмента.
- •Место менеджера в структуре независимой коммерческой фирмы
- •Глава II. Функции управления
- •2.1. Традиционные функции управления.
- •2.2. Рыночные функции управления.
- •Варианты геометрии координационной деятельности
- •Методов управления
- •Глава III. Системный подход к управлению рынком.
- •3.1 Иерархия цели
- •3.2. Иерархия структуры
- •3.3. Иерархия процессов принятия и реализации управленческих решений.
- •Ключевые слова:
- •Литература по I части.
- •Часть II. Базовые условия совершенствования управления рынком
- •Глава IV. Необходимость совершенствования управления
- •Рынком в странах снг
- •4.1 Изменение масштабов производства в экономике.
- •4.2. Формирование многоукладной экономики и рыночных отношений.
- •4.3. Особенности торгово – экономических связей.
- •Географическая структура импорта Азербайджанской Республики
- •Географическая структура экспорта Азербайджанской Республики (2)
- •Динамика добычи нефти в приграничных с Азербайджаном странах (млн. Тонн)
- •Глава V Объективные предпосылки совершенствования управления торговлей
- •5.1. Изменения розничного товарооборота.
- •5.2. Изменения первичных организационных образований торговли
- •5.3. Переход торговли на путь интенсивного развития.
- •5.4 Ускорение темпов научно – технического прогресса в торговле и инновационный менеджмент
- •5.5. Подготовка управленческого персонала в торговле.
- •5.6. Стратегия формирования рынка потребительских товаров и бизнес
- •Структура рынка
- •Показатели, используемые при выявлении рыночных сегментов потребителей (27)
- •Ключевые слова:
- •Литература по II части
- •Часть III. Методы управления рынком.
- •Глава VI. Этапы и методы совершенствования управления рынком.
- •6.1. Подготовительный этап перехода к рынку.
- •6.2. Выбор методов совершенствования управления
- •6.2.1. Экспертные оценки.
- •Шкала «весов» экспертов
- •6.2.2. Организационное моделирование
- •6.2.3.Экономико – математический метод моделирования организации управления рынком
- •6.2.4. Этап осуществления анализа и синтеза управления.
- •Глава VII. Комплексный подход к методам управления рынком
- •7.1. Маркетинг как метод управления рынком
- •7.2. Рыночные и маркетинговые исследования
- •Частота проведения отдельных маркетинговых исследований
- •Ключевые слова:
- •Литература по III части
- •Часть IV. Практика управления рынком
- •Глава VIII. Эволюция и этапы развития управления рынком
- •8.1. Развитие управление рынком (1920 – 1970 гг.)
- •8.2. Исторический анализ управления торговлей в Азербайджанской Республике до завоевания суверенитета
- •8.3. Система управления торговлей Азербайджанской Республики в переходной период к рынку (1991 – 2000 гг.)
- •Примерная индивидуальная структура управления основных и дополнительных типов организации и объединений торговли для г. Баку на 1 этапе переходного периода к рынку
- •Примерная индивидуальная структура управления торговлей г. Баку на 2 этапе перехода к рынку
- •Ключевые слова:
- •Литература к IV части
- •Часть V. Современное управление рынком
- •Глава IX. Современное состояние и информационная база систем управления рынком
- •9.1. Информационная база как основа формирования
- •Системы управления рынком
- •Основные макроэкономические показатели Азербайджанской Республике
- •Распределение трудоспособного населения Азербайджанской Республики занятых в экономике (тыс.Чел.)
- •Удельный вес убыточных предприятий по отраслям экономики, в %
- •Предпринимательская деятельность малых предприятий в 2003 (млрд.М.)
- •Основные показатели торговли Азербайджанской Республик (в млрд. Манат)
- •Индекс потребительских цен в Азербайджанской Республике (в% к предыдущему году)
- •Денежные доходы и расходы населения в Азербайджанской Республике (в млрд. Манат)
- •Оборот внешней торговли Азербайджанской Республики (тыс.Долл. Сша)
- •9.2. Современное состояние и органы управления рынком в Азербайджанской Республике (2000 – 2005 гг.)
- •Заместитель министра
- •Управление делами
- •Центр экспертизы
- •9.3. Особенности информационной базы системы управления рынком в странах снг
- •Удельный вес основных социально – экономических показателей стран снг в % к общему итогу на 2003 г. (1)¹
- •Среднемесячная номинальная заработной плата и их индексы в странах снг (в долларах сша и процентах к предыдущему году) (1)
- •Индексы промышленной и сельскохозяйственной продукции по странам снг (в % к предыдущему году) (1)
- •Индексы вложенных инвестиций в основной капитал по странам снг (в процентах к предыдущему году) (1)
- •Индекс розничного товарооборота по всем каналам продажи в странах снг (в процентах к предыдущему году)
- •Ключевые слова:
- •Литература по V части
- •Часть VI. Управление субъектами рынка
- •Глава X. Комплексный анализ управления субъектов рынка
- •10.1. Методика анализа управления торговых фирм
- •10.1.1. Анализ функциональной структуры
- •А. Функциональные подсистемы
- •10.1.2. Анализ информационной структуры
- •В аппарате управления торговой формы
- •10.1.3. Социологический анализ структуры
- •Полномочий в аппарате управления торговой фирмы
- •Распределение времени на выполнение функций управления среди руководящих работников аппарата управления торговых фирма (%)
- •Степень принятия окончательного решения руководителем торговой фирмы в целом и отдельных ее подразделений (%)
- •Распределение вида ответственности и полномочия среди руководящих работников торговых фирм
- •2. Структура результатов, докладываемых в вышестоящие инстанции
- •3. Структура затраты времени на мероприятия, проводимые непосредственным руководителем, подчиненными, другими подразделениями, самостоятельную и внеплановую работы.
- •10.1.4. Зарубежный опыт анализа структуры
- •1). Рационализация вертикального управления
- •2). Рационализация управления коммерческой деятельностью
- •3) Хозяйственные центры как инструмент воздействия на аппарат управления торговой фирмы
- •3). Организация управления и информационная система в торговле
- •4) Некоторые аспекты организационного проектирования торговых фирм
- •И ее методологические требования
- •10.2. Совершенствование и оптимизация управления торговых фирм
- •Логическая таблица (лт – 1)
- •Логическая таблица (лт – 2) переходного периода к рынку
- •Торговой фирмы в условиях перехода к рынку
- •Группировка торговых фирм по степени организованности структуры, сложности структуры управления и показателя уровня организации, предлагаемых для переходного периода к рынку.
- •Глава XI . Особенности управления коммерческой деятельностью торговых фирм
- •11.1. Коммерческая фирма как сложный субъект рынка
- •Подход немецких ученых к классификации типов фирм
- •Преимущества и недостатки специализации (29)
- •1. Эволюция торговых фирм
- •2. Полномочия управляющих отношениями с основным клиентом
- •Коммерческие фирмы
- •11.2. Специфика управления коммерческой деятельностью
- •Характеристика организационных форм коммерческой деятельности
- •Концепция традиционной организации
- •Ключевые слова
- •Литература по VI части
- •Часть VII. Проблемы моделирования управления рынком
- •Глава XII. Теоретические аспекты моделирования организационных структур
- •12.1. Классификация и подходы к моделям формирования организационных структур управления
- •Иерархической структуры
- •12.2. Диагностика влияющих факторов организации управления на основные экономические показатели торговли
- •Корреляционная матрица между показателями и факторами, а также между самими факторами торговой системы
- •Результаты расчетов по определению относительных погрешностей на уровне торговой системы
- •Корреляционная матрица между показателями и факторами, на уровне основного звена управления
- •Результаты расчетов по определению погрешностей на уровне основного звена управления
- •Глава XIII. Оптимизация и определение экономической эффективности управления торговлей
- •Анализ согласованности исходной информации и определение взаимовлияний
- •Группирование показателей оценки значимости влияния факторов по торговой системе в условиях переходного периода к рынку
- •Группировка показателей оценки значимости влияния факторов на уровне основного звена управления (фирмы) в условиях переходного периода к рынку
- •13.2. Определение оптимальных значений и критерий эффективности основных экономических показателей и элементов организации управления торговлей.
- •Определение минимальных средних и максимальных величин основного звена управления (фирмы)
- •Расчетные значения функций принадлежности по ограниченному кругу факторов основного звена управления (фирмы), влияющих на у¹
- •Расчетные значения функций принадлежности факторов в целом основного звена управления (фирмы), влияющих на у¹
- •Расчетные значения функции принадлежности факторов основного звена управления (фирмы), влияемых на у²
- •Расчетные значения функции принадлежности факторов основного звена управления (фирмы), влияющих на у³
- •Расчетные значения функции принадлежности факторов торговой системы, влияющих на у¹
- •Расчетные значения функции принадлежности факторов торговой системы, влияющих на у²
- •Расчетные значения функции принадлежности факторов торговой влияющие на у³
- •Ключевые слова:
- •Литература по VII части
- •Основные исходные данные организации управления по торговой отрасли.
- •Основные исходные данные организации управления на уровне торговых фирм
- •Понятийный аппарат
- •Отраслевые рынки в структурно-логических схемах (Учебно-наглядный материал для студентов, магистрантов и аспирантов)
- •Ыы. Назирилийин ясас вязифяляри.
- •Ыыы. Назирлийин функсийалары
- •Ыв. Назирлийин щцдуглары
- •В.Назирлийин фяалиййятинин тяшкили
- •Ыы. Департаментинин ясас вязифяси
- •Ыыы. Департаментин функсийалары
- •Ыв. Департаментин фяалиййятинин тяшкили
- •В. Департаментин ишчиляринин мясулиййяти
- •Базарын идаря едилмяси
Иерархической структуры
Сущность данного метода состоит в поиске разложения и описывается следующим образом:
A=
![]() λkX
+μ1+
λkX
+μ1+
где I – тождественная матрица;
– остаточная матрица ошибок;
λk,μ – оцениваемые параметры, определяемые методом наименьших квадратов.
Большой интерес вызывают с модели шестой группы, разрабатываемые на основе так называемых «эталонных структур» (7). Этот принцип осуществляется таким образом, что эталонная структура описывается в виде разветвляющегося вниз графа, вершиной которого является распределительный центр (РЦ), а ребра характеризуют отношения подчинения. Параметрами эталонной структуры выступают:
m(μ) – число управляющих вершин РЦ;
n(μ) – максимальное число уровней распорядительства;
k(μ) – размах контроля на i – м уровне распорядительства (i = 1,2....n).
В результате делается вывод, что эталонная структура тогда будет полной, если число уровней распорядительства одинаково по всем ответвлениям иерархического дерева.
Ценность седьмой группы моделей заключается в том, что анализ сложных организационных структур осуществляется методом имитации (8). В качестве организационных моделей выбран простейший случай системы линейного двухпараметрического регулирования с иерархической структурой.
Первые семь групп моделей, в основном, включают один обобщенный критерий, характеризующий оптимальность функционирования организационной структуры управления. Однако существуют мнения о том, что моделирование организационной структуры управления необходимо производить по отдельным подсистемам, взаимосвязанным между собой, которые составляют восьмую группу моделей. (9)
При этом выделяют следующие основные подсистемы организационной структуры с последующим моделированием: формальная структура, неформальная структура, информационная структура, функциональная структура, квалификационная структура, структура технических средств.
Одна из моделей подсистем, например, основывается на распорядительно – контрольной функции и определяется следующим образом:
ФPKH=![]() Pkni+
Pkni+![]() PkHi+
Иn,
PkHi+
Иn,
где ФpkH – распорядительно – контрольная функция руководителя;
n – количество работников подразделения (подчиненных);
m – число контролируемых распоряжений;
Pkni – контролируемые распоряжения (изъятие инициативы исполнителя);
PkHi – неконтролируемые распоряжения (делегирование или инициативы от руководителя к исполнителю);
Иn – контроль исполнения распоряжения.
Весьма существенными является модели девятой группы, сущность которых заключается в взаимосвязанности различных объектов – отраслей предприятий и т.д. (10). В данном случае при формировании организационных структур управления предлагают две модели: первая, отражает декомпозицию сложной системы на подсистемы, вторая – выявление скрытых резервов организационных систем.
При решении первой модели используют распространенный количественный критерий, связанный с понятием близости элементов системы. Элементами близости, например, может выступать величина потоков информации между подсистемами и по другим признакам. Для определения меры близости между предприятиями авторы предлагают использовать общий коэффициент близости, учитывающий как количественные, так и качественные признаки совместно по следующей формуле:
Cij=
![]() Cij
+
Cij
+
![]() ·
·
![]() ij
,
ij
,
где n – множество признаков;
nи - количественные признаки;
n - nи - качественные признаки;
ij – коэффициент Танимато – Роджерса;
ij – мера связанности с использованием методики абсолютных значений.
Модели девятой группы дают возможность формировать организационную структуру управления не только предприятия, но под отрасли или даже отрасли в целом.
И наконец, десятая группа моделей в определенной мере решают вопросы формирования организационной структуры управления органов планирования и управления высшего звена и межотраслевых народнохозяйственных комплексов, также основанных на коэффициентах близости и с помощью специальных алгоритмов (2).
В частности при этом в качестве меры близости используется взвешенный коэффициент Танимато – Роджерса:
a1q · aiq

![]() Nq
Nq
 P(n) =
P(n) =
+
-

 Nq
Nq
Nq
Nq
Nq
Nq
где Nq– число элементов обладающих qm признаком,
a1 – i-й мерный ноль – единичный вектор;
( a1q · aiq) ai – q-я компонента n-го вектора – количество признаков, которыми одновременно обладают оба элемента;
a1q – количество признаков, которыми обладает i-й элемент.
Далее используется следующая блок – схема алгоритма (см. рис. 7.2.).











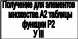



Рис. 7.2. БЛОК – СХЕМА АЛГОРИТМА
