2. Информация, сообщение, сигнал. Структура системы передачи информации. Количественное описание объема и скорости передачи информации.

(виды сигналов см. в теме 2 вопросе 5)

Информация, сообщение, сигнал.

Информация – это совокупность знаний об окружающем мире и процессах его изменения.

Передача информации происходит в виде передачи сообщений (набор символов, цифровых данных, звуков, изображений). Передача сообщений на расстояние производится с помощью реальных материальных носителей - сигналов (электромагнитных колебаний, радиоволн, световых импульсов) по физическим каналам связи.

Сигнал (от лат. signum – знак) – физический процесс, несущий информацию и изменяющийся во времени и пространстве.

Сигналы бывают электрические, радиоволны, звуковые, световые и др. В радиотехнике сигнал – это электрические поля, изменяющиеся во времени.

Структура системы передачи информации.

Транспорт информации (сигналов) осуществляется по каналам связи. Например, в радиотехнике носителем информации (сигналов) являются радиоволны на конкретной несущей частоте. Они только переносят информацию, т.е. являются физическим каналом связи. Сами информационные сигналы передаются в виде изменения характерных параметров радиоволн - амплитуды, частоты или фазы.

Структурная схема системы передачи информации по радиоканалу приведена на рис. 3.2. На рисунке приняты следующие обозначения: ИС- источник сообщения, КД - кодирующее устройство (кодер), ГВЧ - генератор высокой частоты, М - модулятор, УМ - усилитель мощности, далее волновой канал связи, А1 и А2 - антенны, ДМ - демодулятор, ДК - декодер, ПС - получатель сообщения.

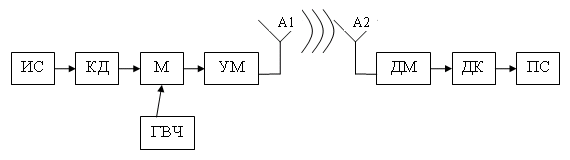
Рис. 3.2. Структура системы передачи информации по радиоканалу

Количественное описание объема и скорости передачи информации.

(часть 1, 3 – точно нужно, часть 2 – может, и не нужно)

Часть 1:

Количественная оценка информации

Единицей количества информации в бинарном сообщении является 1 бит (состояние 0 или 1). Это количество информации содержится в сообщении из одного знака, который может принимать значение 0 или 1. Такой знак называется двоичным (бинарным), так как он может принимать только два значения. Другие знаки (буквы и десятичные цифры) и символы передаются в виде набора (последовательности) из m двоичных знаков (разрядов). Обычно используют 4-х , 8-ти ,10-ти, 12-ти и 16-ти разрядные двоичные коды.

При равной вероятности событий 0 и 1 в одном двоичном знаке имеем: Р(0) = Р(1) = 0,5.

Из множества неравновероятных событий {a_i} с вероятностями появления событий P(a_i)=P_i , причем P_i1, логично предположить, что чем меньше вероятность P_i возникновения события a_i, тем больше информации мы получаем при его появлении.

Американский математик Шеннон предложил оценивать количество информации при появлении события a_i величиной:

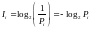. (3.1)

Часть 2:

Наряду с количеством информации, в теории информации используют понятие энтропии как меры неопределенности информации. При этом появление события a_i снимает неопределенность (энтропию).

Энтропия источника сообщения способного выдать N вариантов событий a_i в сообщении составит:

. (3.2)

Количество информации в одном бите, содержащееся в единичном сообщении о наступлении одного из двух равновероятных событий P₁=P₀=0,5 можно оценить через энтропию по формуле (3.2):

Событие бит.

В этом выражении мы видим, что появление события 0 или 1 снимает неопределенность в 1 бит. Получаем тот же результат, что и по формуле (3.1): при равновероятных событиях появление 0 или 1 несет информацию равную I₁=log₂2=1 бит.

Таким образом, при одном двоичном сообщении (событии) получаем информацию равную 1 биту и полностью ликвидируем неопределенность (энтропию) в 1 бит.

Последовательная передача m двоичных равновероятных событий даёт объем информации I = m I₁ =H∙m = m бит.

Если каждый знак (символ) a_i из множества неравновероятных событий {a_i} выражен l двоичными знаками, то вероятность P(a_i)=P_i появления определенного знака a_i в m событиях будет обратно пропорциональна числу сочетаний из m элементов по l. Число сочетаний из m элементов по l в m составляет N_l= l^m .

Используя формулу (3.1), с учетом 1/P_i =N_i= l^m находим количество информации в сообщении, переданном одним знаком:

I₁= log₂ l^m=m log₂ l . (3.3)

Скорость передачи информации

Во многих случаях информация по каналу связи передаётся в двоичной системе в битах (binary digit) (0 или 1). Обычно используют каналы с двухуровневыми значениями: ноль (0) или единица (1). Например, логический ноль в транзисторно-транзисторной логике (ТТЛ логике) соответствует напряжению от 0 до 2,5 В, а логической единице ставится в соответствие напряжение от 2,5 до 5,5 В.

Вместе с тем, есть каналы передачи с тремя (-1, 0, +1 В) и пятью уровнями градаций напряжения (-3,5; -0,7; 0; 0,7; 3,5 В).

Если для передачи символа ai (цифры или буквы) используют m-градаций, то объём информации, переданный одним символом, составит log2 m бит.

Объём передаваемой информации за время Т будет:

Q= Nlog2 m = (T/T)log2 m,

где N= T/T - число символов за время Т, ΔТ - длительность передачи одного символа ai.

Если десятичное число градаций m перевести в двоичное число, то получим число двоичных разрядов, необходимых для представления этого числа, т.е. число log2 m соответствует числу двоичных разрядов, необходимых для передачи символа ai. Используя последнее выражение можно оценить среднюю скорость передачи информации в интервале времени Т.