
- •Физические основы деформирования и разрушения твердых тел.
- •1.Напряжения
- •Деформации.
- •3. Соотношение между напряжениями и деформациями в идеально-упругой среде.
- •4. Деформирование горных пород
- •4.1 Полные диаграммы деформирования и разрушения горных пород при одноосном сжатии и растяжении
- •4.2 Деформируемость и прочность породных массивов.
- •5. Теории разрушения.
- •5.1 Теория Кулона.
- •5.2 Теория Кулона - Навье.
- •5.3 Теория Мора.
- •5.4 Критерий пластического течения.
- •6. Теоретическая прочность.
- •7. Теория Гриффитса.
- •8. Распределение напряжений вокруг вершин острых трещин.
- •8. Распределение напряжений в окрестности вершин трещин при действии сжимающего напряжения
- •9. Влияние слабых плоскостей на разрушение твердых тел.
- •10. Распространение трещин в горных породах.
- •11. Об элементарных актах процесса, ведущего к разрушению твердых тел
- •12. Кинетическая теория прочности.
- •12.1 Тепловые флуктуации и их роль в процессе разрушения. Физический смысл величин τ0 и u0
8. Распределение напряжений в окрестности вершин трещин при действии сжимающего напряжения
Рассмотрим идеально узкую трещину
длинной
![]() .
Если к площадке с трещиной приложено
одноосное сжимающее напряжение
,
то на поверхности трещины будет
действовать касательное
.
Если к площадке с трещиной приложено
одноосное сжимающее напряжение
,
то на поверхности трещины будет
действовать касательное
![]() и нормальное напряжение принимается
что, нормальное напряжение не будет
влиять на распределение напряжений
около идеально тонкой (закрытой) трещины
и следовательно, можно считать, что на
поверхности трещины приложено только
касательное напряжение (чистый сдвиг)
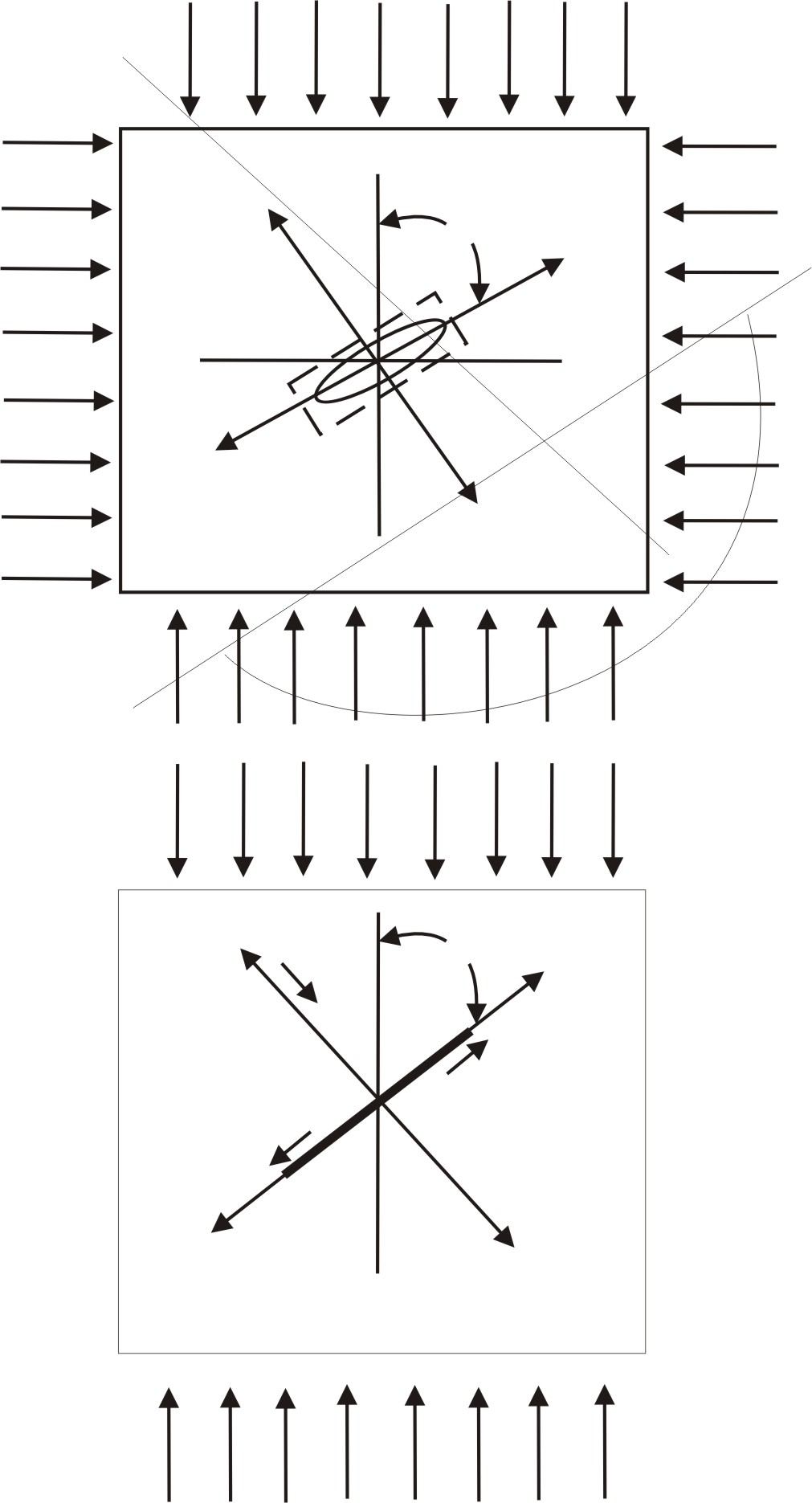
(рис 8.1). В этом случае компоненты
напряжений у кончика трещины равны (рис
8.2)
и нормальное напряжение принимается
что, нормальное напряжение не будет
влиять на распределение напряжений
около идеально тонкой (закрытой) трещины
и следовательно, можно считать, что на
поверхности трещины приложено только
касательное напряжение (чистый сдвиг)
(рис 8.1). В этом случае компоненты
напряжений у кончика трещины равны (рис
8.2)
![]()
![]()
![]()
![]()

![]()
![]() В
кончике трещины имеется особенность
(
В
кончике трещины имеется особенность
(![]() )
и напряжения бесконечны. Однако, если
учесть, что при высоких напряжениях
горные породы пластичны в области r1<r2,
то уравнениями можно пользоваться в
области r1>r2.
Наиболее неблагоприятной ориентацией
трещины будет ориентация, при которой
)
и напряжения бесконечны. Однако, если
учесть, что при высоких напряжениях
горные породы пластичны в области r1<r2,
то уравнениями можно пользоваться в
области r1>r2.
Наиболее неблагоприятной ориентацией
трещины будет ориентация, при которой
![]() максимально. Так как
максимально. Так как
![]() ,
то
,
то
![]() при
=45.
при
=45.
Максимальное и минимальное напряжения в области r1>r2 около кончика трещины определяется:
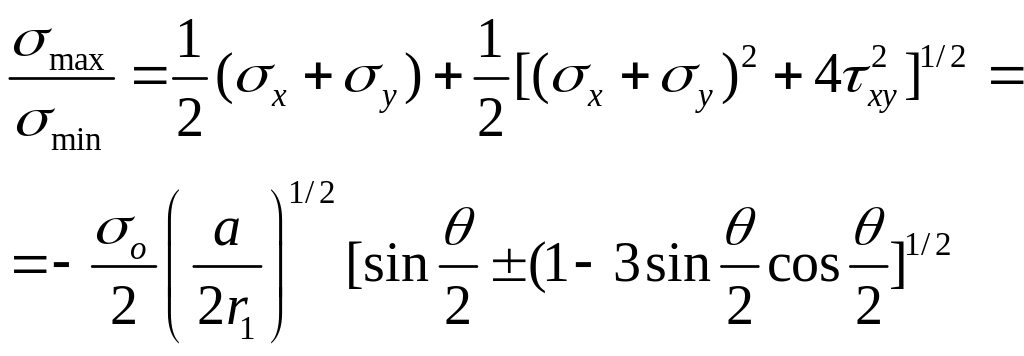
![]()
П
ри
![]()
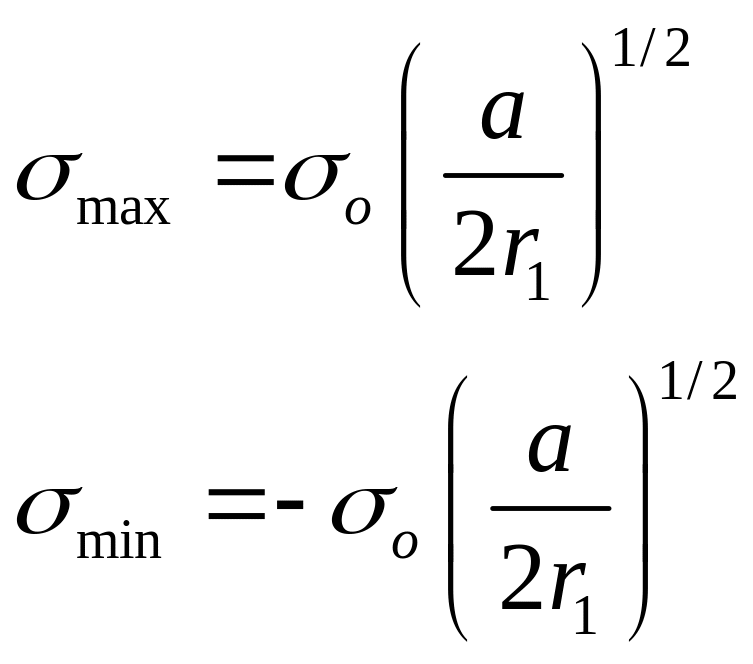
Н
аправление
![]() и
и
![]() определяется уравнением:
определяется уравнением:
![]()
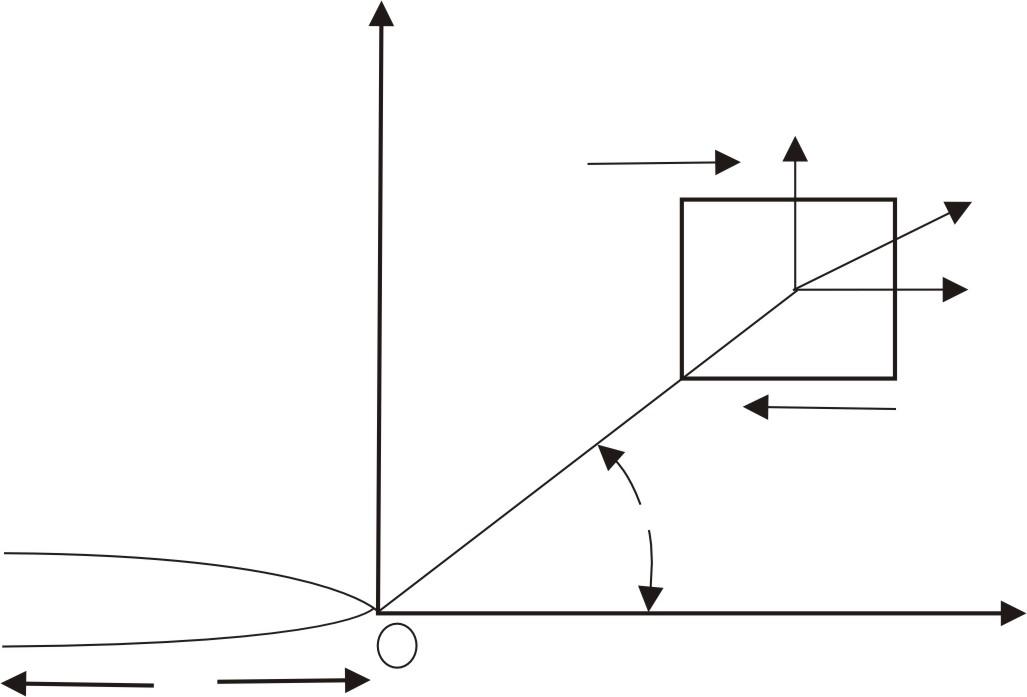
рис. 8.1
Напряжения в
окрестности вершин трещины
при действии
сжимающих напряжений
П
ри
![]() и
и
![]() =0,
или
=0
=0,
или
=0
Э
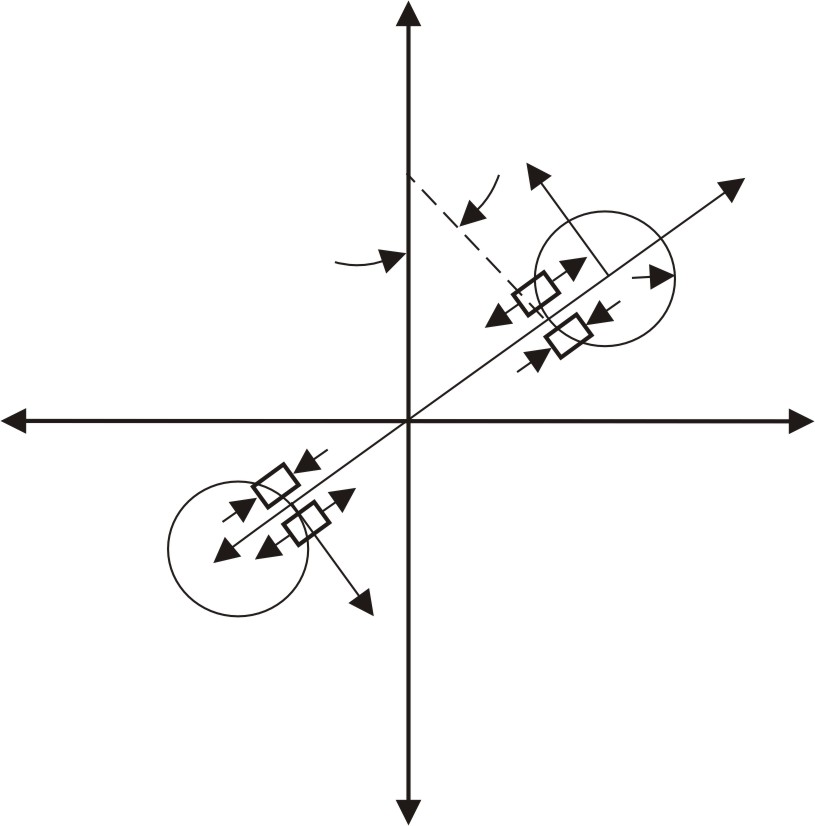
рис. 8.2
Напряжения в
окрестности вершин трещины![]() ти
результаты означают, что наиболее
неблагоприятной ориентацией трещины
под углом 45o к
направлению прикладываемого одноосного
напряжения. Если выделенный при r=r1
элемент повернуть на угол
ти
результаты означают, что наиболее
неблагоприятной ориентацией трещины
под углом 45o к
направлению прикладываемого одноосного
напряжения. Если выделенный при r=r1
элемент повернуть на угол
![]() ,
то максимальное (растягивающее)
напряжения, действующее на этот элемент,
будет направлено по оси x.
,
то максимальное (растягивающее)
напряжения, действующее на этот элемент,
будет направлено по оси x.
Е
![]()
 сли
это напряжение превышает предел прочности
породы, то трещина начнет двигаться в
направлении, перпендикулярном направлению
действия этого напряжения, т.е. в
направлении y или под
углом 45o к направлению
приложенного напряжения
(рис
8.3). Если элемент при r1
повернуть на угол
сли
это напряжение превышает предел прочности
породы, то трещина начнет двигаться в
направлении, перпендикулярном направлению
действия этого напряжения, т.е. в
направлении y или под
углом 45o к направлению
приложенного напряжения
(рис
8.3). Если элемент при r1
повернуть на угол
![]() ,
то на этот элемент будет действовать
сжимающее напряжение в направлении оси
X.
,
то на этот элемент будет действовать
сжимающее напряжение в направлении оси
X.
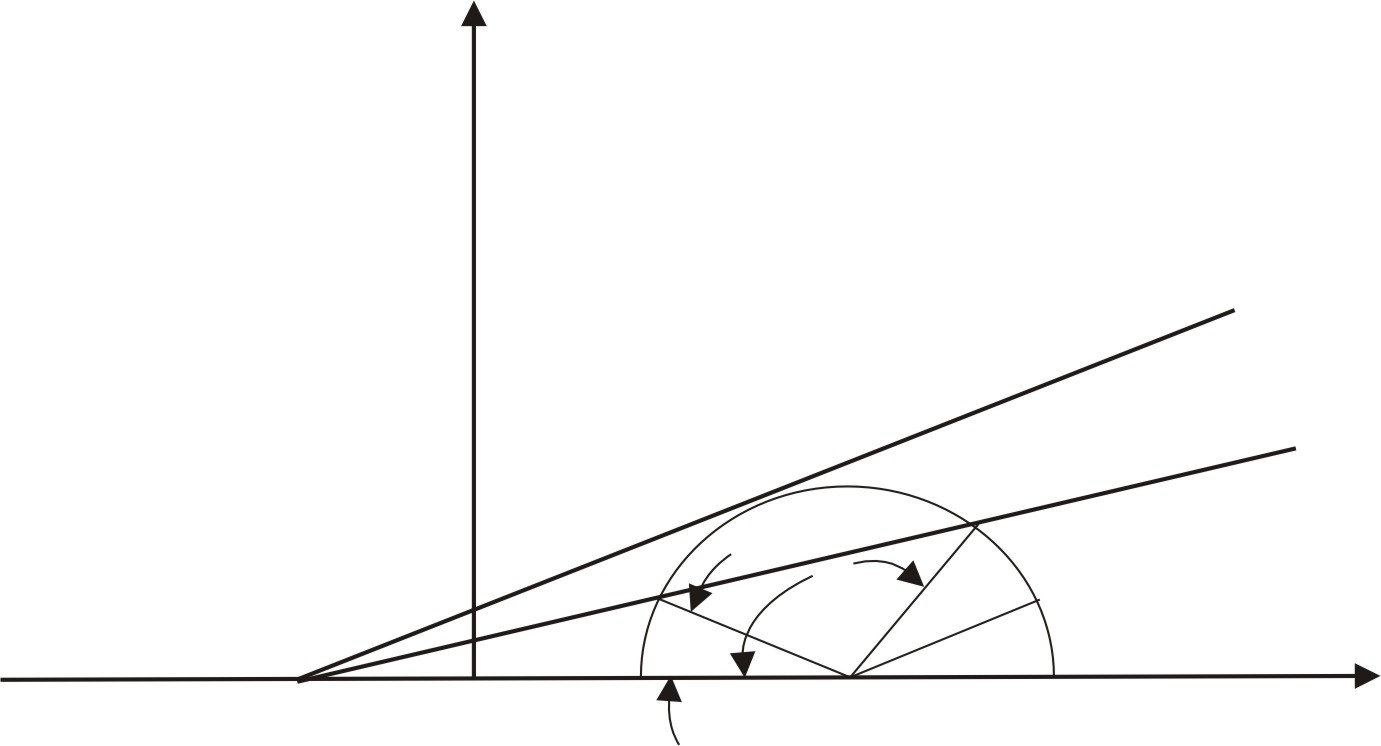
![]()
рис. 8.3
Ответвляющиеся
трещины, образующиеся у концов начальной
трещины в сжимающем поле напряжений
9. Влияние слабых плоскостей на разрушение твердых тел.
В макроскопическом масштабе большинство горных пород содержит слабые плоскости, которые влияют на механические свойства пород, делая их механически анизотропными. Кроме того, имеется анизотропия в строении минералов (слоистость и др.), которая может сказываться на свойствах пород в макроскопическом и мегаскопическом масштабах. Этими слабыми плоскостями могут быть спаи, сбросы, трещины, а в породах состоящих из пластов, и в слоистых породах - прослойки между пластами и слои с более низкой прочностью.
Р
рис. 9.1
Спай в объеме
горных пород
поверхность
разрушения

![]()
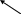
 ассмотрим
объём ГЦ, содержащий спай, ориентированный
под углом φ к направлению
наибольшего сжимающего напряжения σ1
(рис 9.1) и пусть огибающая Мора для
сплошной породы представлена линией
(рис. 9.2), а для породы со спаем - линией
CD. Для данной системы
приложенных напряжений с кругом Мора
(σ3 σ1)
и при ориентации трещины под таким углом
ψ, что 2ψ<2ψ1
или больше π-2β2
порода будет разрушаться перпендикулярно
плоскости спая. Если же 2β
лежит между 2β1 и
2β2, то порода будет
разрушаться по плоскости спая. Если
коэффициент внутреннего трения μ
=tgφctg2ψ для
спая существенно меньше, чем для породы,
то область возможных углов, для которых
разрушение будет происходить в
перпендикулярном к плоскости спая
направлении, а не вдоль него, сильно
ограничена.
ассмотрим
объём ГЦ, содержащий спай, ориентированный
под углом φ к направлению
наибольшего сжимающего напряжения σ1
(рис 9.1) и пусть огибающая Мора для
сплошной породы представлена линией
(рис. 9.2), а для породы со спаем - линией
CD. Для данной системы
приложенных напряжений с кругом Мора
(σ3 σ1)
и при ориентации трещины под таким углом
ψ, что 2ψ<2ψ1
или больше π-2β2
порода будет разрушаться перпендикулярно
плоскости спая. Если же 2β
лежит между 2β1 и
2β2, то порода будет
разрушаться по плоскости спая. Если
коэффициент внутреннего трения μ
=tgφctg2ψ для
спая существенно меньше, чем для породы,
то область возможных углов, для которых
разрушение будет происходить в
перпендикулярном к плоскости спая
направлении, а не вдоль него, сильно
ограничена.
Е сли в объёме ГП содержится ряд плоскостей спаев с одинаковыми огибающими, и если круг напряжений пересекает огибающую, то область углов ψ, для которых разрушение не будет происходить в плоскости спая, становится
о
![]()
![]() чень
малой. Для конечного объёма пород с
рядами случайно ориентированных систем
спаев допустимый круг напряжений, т.е.
чень
малой. Для конечного объёма пород с
рядами случайно ориентированных систем
спаев допустимый круг напряжений, т.е.
к
рис. 9.2
Огибающие кругов
Мора при наличии напряжений
