Физические основы деформирования и разрушения твердых тел.

1. Давление, напряжение и деформации.

Взаимодействие в твердых телах приводит к образованию кристаллических решеток. Расположение узлов кристаллических решеток различно в разных направлениях. Поэтому любое усилие извне приводит к изменению расстояния между частицами, зависящее от направления действия силы и положения плоскости, в которой расположены узлы решетки.

Силовое воздействие на твердое тело вызывает изменение взаимного расположения частиц, что может характеризоваться изменением объема среды и его формы. До тех пор, пока не происходят необратимые нарушения в среде, после снятия нагрузки частицы возвращаются в исходное состояние.

В газообразных и жидких средах ближнее взаимодействие между частицами нарушается настолько, что кристаллическая структура утрачивается. В этом случае результат силового воздействия на среду не зависит от направления приложения сил.

В таких средах силовое взаимодействие между частицами определяет величину давления.

Давление есть сила, действующая на единичную площадку со стороны выделенного в среде объема. Эта сила не зависит от направления и является скалярной величиной.

1.Напряжения

П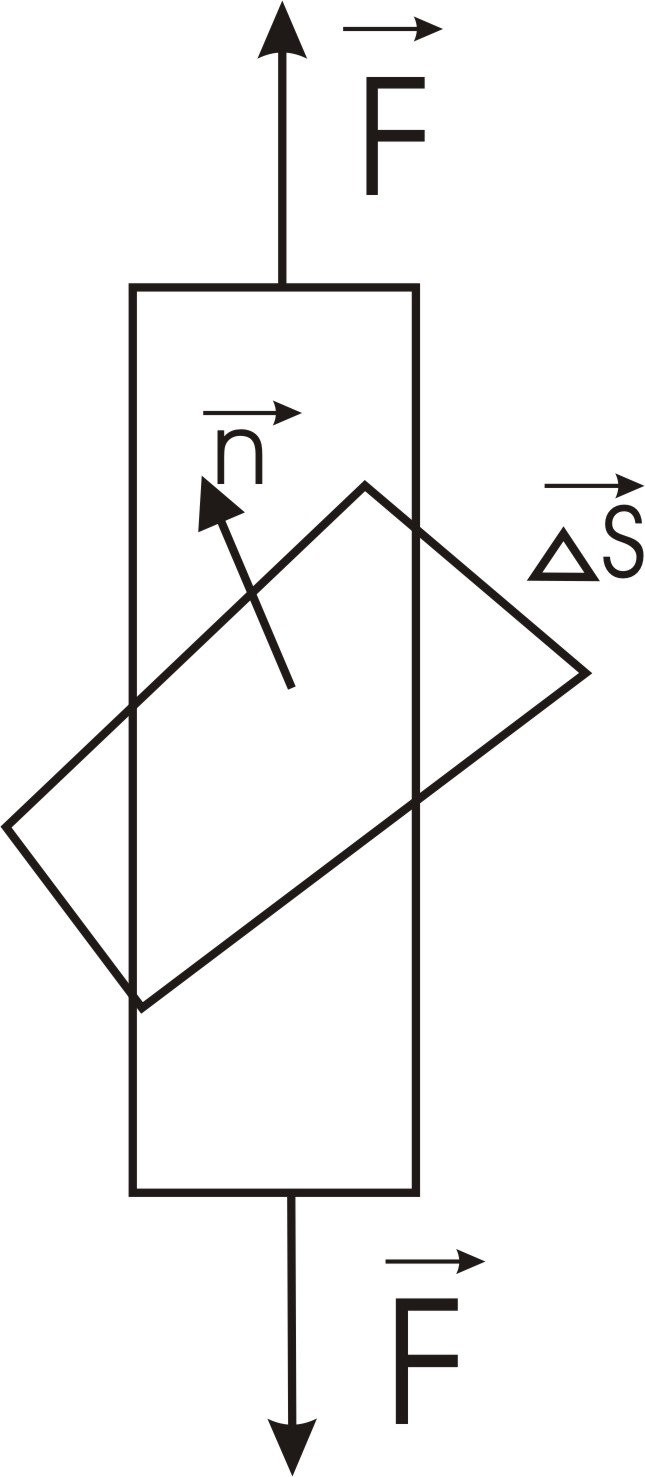 од напряжением понимается внутренняя сила действующая на единицу площади, имеющей определенную пространственную ориентацию (рис.1)

при

Сила величина векторная имеет три компоненты, например F_x,F_y,F_z.

Ориентация площадки определяется направлением единичного вектора .

П

Рис.1

Действие силы

на площадку

усть на стержень действует растягивающая сила . Очевидно, что величина напряжения зависит от направления силы по отношению к плоскости. Поэтому для задания напряжения необходимо знать не только величину, линию действия и направление силы, но также и положение в пространстве площадки, на которую она действует. Поэтому напряжение является тензором – для его определения нужно знать вектор силы и вектор, характеризующий положение площадки.

В прямоугольной системе координат сила полностью определяется ее компонентами вдоль трех осей F_x,F_y,F_z. Кроме того, необходимо ввести индекс, соответствующий направлению нормали к плоскости площадки.

Напряжение в сечении, проходящем через некоторую точку, можно разложить на две составляющие – нормальное, перпендикулярное к сечению, и касательное, в плоскости сечения. Направление нормальной составляющей является вполне определенным, здесь достаточно одного индекса, обозначающего направление нормали к площадке.

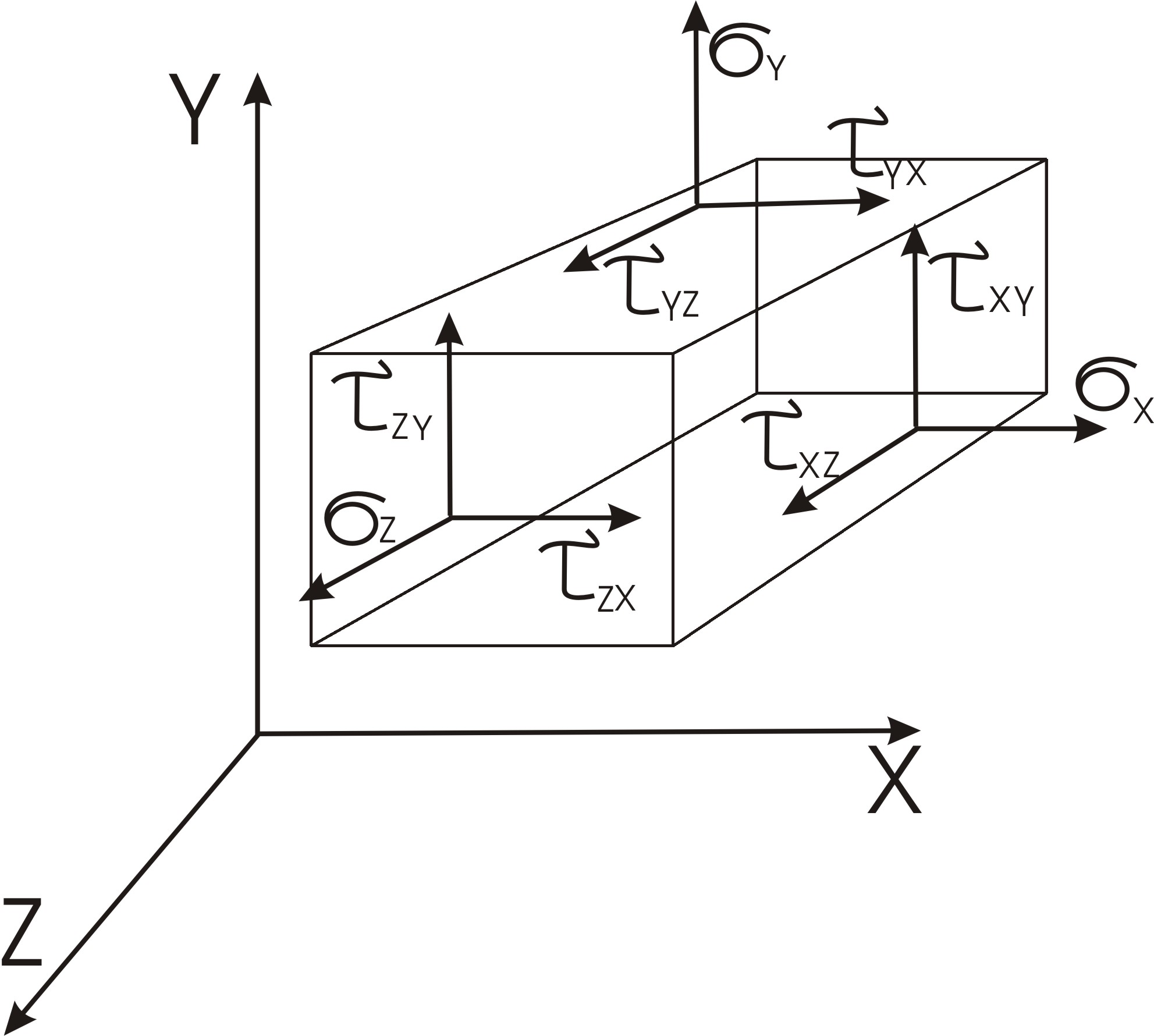Касательную составляющую можно разложить на две составляющие, параллельные координатным осям.

Таким образом, тензор напряжения имеет 9 составляющих (Рис. 2) – 3 нормальных по отношению к координатным плоскостям и 6 касательных и является тензором напряжений второго ранга. Он записывается в виде:

Рис.2

Компоненты напряжений

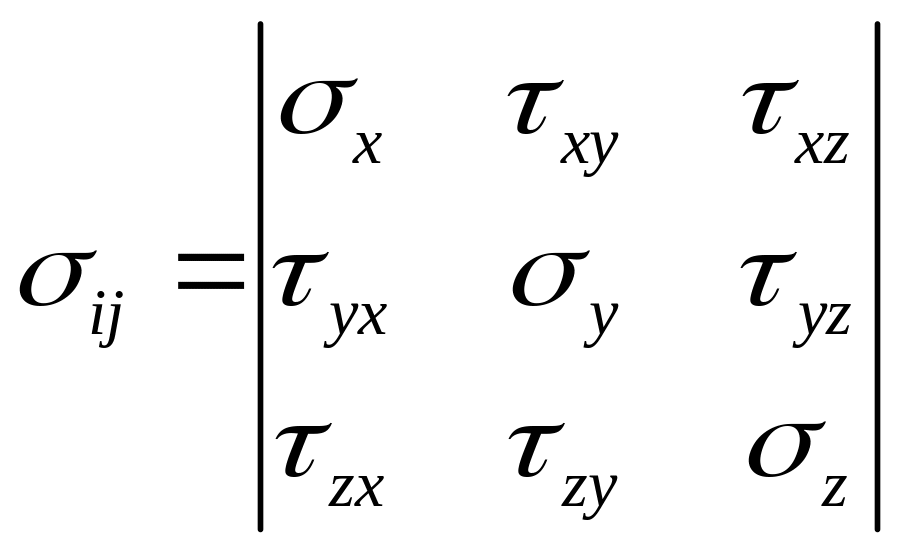
Поскольку выделенные участки тела находятся в равновесии, то две составляющие тензора напряжений направленные к одной и той же грани должны быть равны друг другу:

, ,

Таким образом, тензор напряжений является симметричным.

Напряженное состояние тела полностью определено, если известны значения шести компонентов напряжений в каждой точке. Зная компоненты в точке тела, можно вычислить напряжения в любой площадке проходящей через эту точку перпендикулярно к плоскости xy и наклоненной к осям x и y. Наиболее просто нахождение новых компонентов напряжений может быть рассмотрено для плоского напряженного состояния. В этом случае

Для площадки, нормаль к которой составляет угол с осью x может ?? быть новая координатная система с осями , . Ось направлена нормали к площадке (рис. 3).

В новой системе координат компоненты напряжений составят , определяемые соотношением:

(1.2)

(1.3)

(1.4)

Таким образом, величины , , меняются в зависимости от угла . При определенных значениях величины , могут достигать минимума или максимума. При минимальном значении величина будет максимальной. Экстремальные значения , определяются условиями

Дифференцируя выражения (2) и (3) получим:

(1.5)

о ткуда (1.6)

Так как , то уравнения (6) дает два взаимных перпендикулярных направления. В одном из них величина

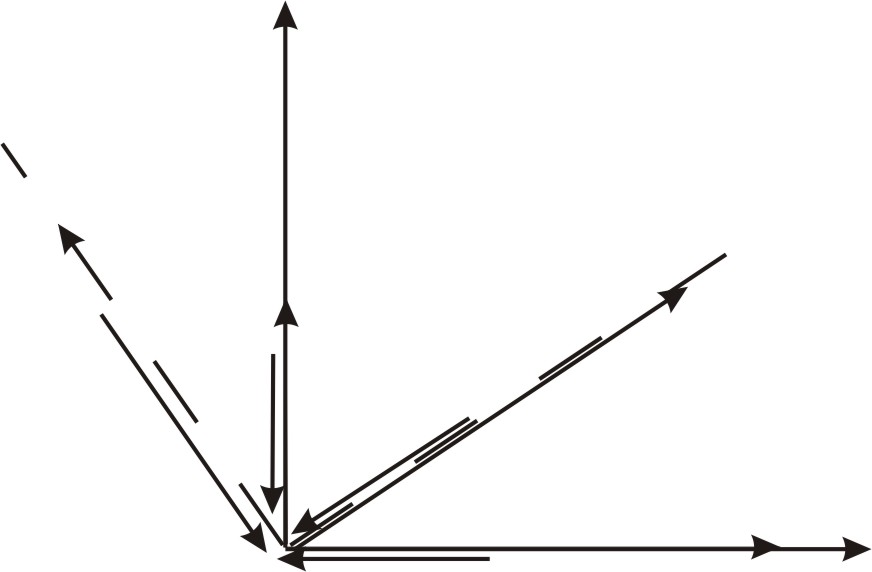
Рис.3 Напряжения в разных системах координат

Из выражений (2) и (3) следует, что . Такое же равенство суммы всех компонентов напряжений справедливо и для более общего трехмерного напряженного состояния:

где - первый инвариант напряжений.

Величину , называют средним нормальным и гидростатическим давлением.

Направления координатных осей, для которых две компоненты нормальных напряжений экстремальны, а касательные напряжения равны нулю, называется главными и обозначаются при этом Касательные напряжения максимальны в направлениях, которые делят пополам углы между главными осями. Их связь с главными нормальными напряжениями и между собой выражается соотношением:

Максимальные значения имеет величина . Если в качестве главных направлений для плоского напряженного состояния приняты оси x и y, то для площадки, нормаль к которой расположена под углом к оси x, компоненты напряжений в соответствии с формулами (2) и (3) определяется соотношением:

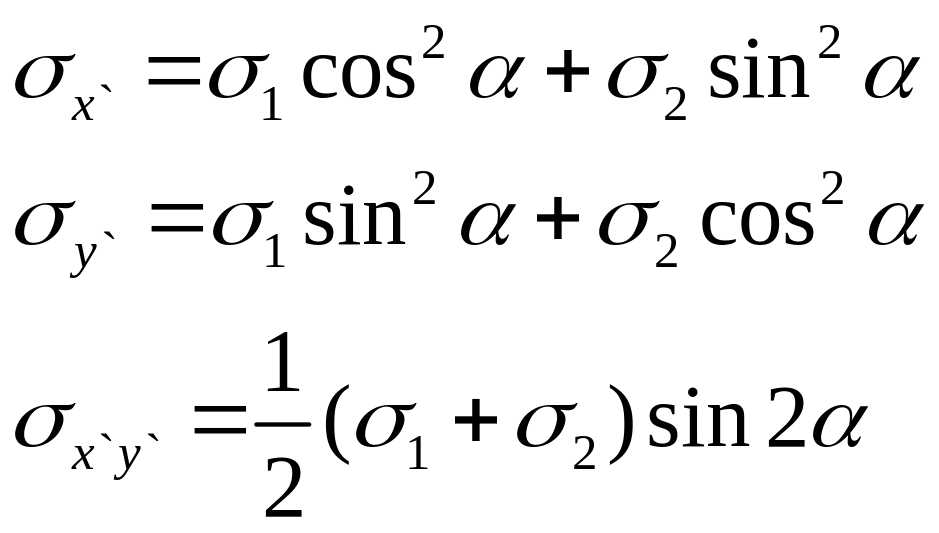(1.7)

Соотношения (17) могут быть представлены в виде:

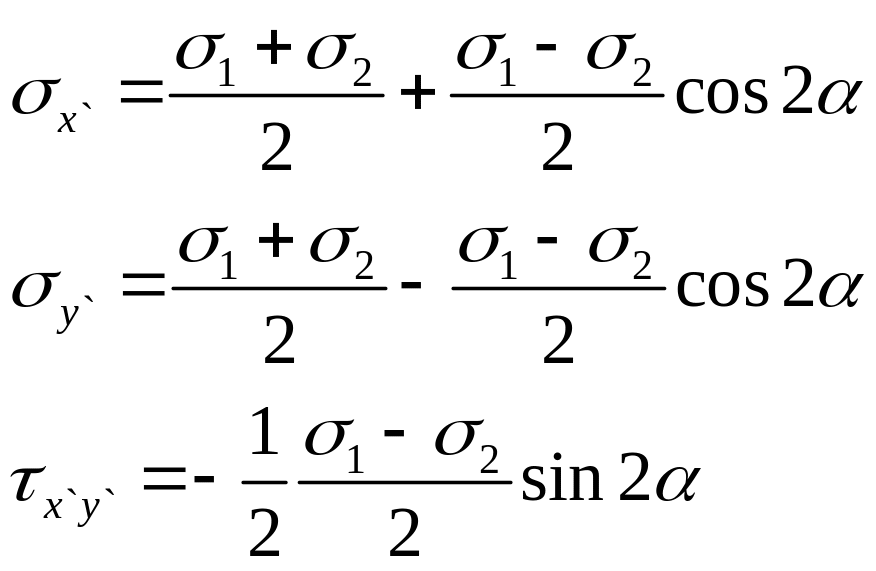(1.8)

Зависимость и от угла можно изобразить с помощью графика, известного под названием круга Мора. Круг Мора строится следующим образом: на горизонтальной оси из произвольной точки O откладываются отрезки OA и OB, пропорциональные соответственно напряжениям и с учетом их знака (рис.4). На рис.4 оба напряжения приняты положительными, т.е. растягивающими. Из точки C, делящий отрезок AB пополам, как из центра, описывается окружность радиусом CA=CB. Полученная окружность и является кругом Мора. В общем случае главные напряжения не являются главными, а известны компоненты , . Тогда на горизонтальной оси откладываются отрезки OF` и OF, соответствующие в выбранном масштабе напряжений и . В точке F` восстанавливается перпендикуляр к OF и на расстоянии, пропорциональном , откладывается точка D`. Величина CD` равна радиусу круга Мора с центром в точке C. Тогда главные напряжения и определяются при пересечении круга Мора с горизонтальной осью, что соответствует величине угла =0. Угол определяется по графику круга Мора: угол между направлениями OC и CD с вершиной в точке C составляет 2 .

2α

Рис.4 Круг Мора