
- •1.Постановка экономической проблемы и ее качественный анализ.
- •2.Построение математической модели.
- •3. Математический анализ модели.
- •4.Подготовка исходной информации.
- •5.Численное решение.
- •6.Анализ численных результатов и их применение.
- •Этапы планирования эксперимента
- •Вид аппроксимирующей функции
. Вычисление статистических моментов
|
Среди множества числовых характеристик изображений, рассматриваемых как реализации случайного поля, выделим несколько наиболее употребительных. Это математическое ожидание (среднее), среднеквадратическое отклонение, коэффициенты асимметрии и эксцесса, энтропия, значения минимального и максимального элементов анализируемого поля и размах (диапазон уровней). Подчеркнем, что здесь и далее речь идет об оценках соответствующих характеристик. Определение статистических характеристик начнем с вычисления начальных и центральных моментов. Момент, рассматриваемый относительно начала координат, называется начальным, а относительно математического ожидания – центральным. В теории вероятностей начальные моменты mk k-го порядка вычисляются по общей формуле
где xi – некоторое значение дискретной случайной величины X; pi = P{X = xi} – вероятность, с которой случайная величина X принимает значение xi.
Математическая
статистика оперирует с оценками
указанных моментов. Применительно к
анализу изображения
В терминах математической статистики множество пикселей, составляющих изображение, являются выборкой. Количество использованных для анализа пикселей будем называть объемом выборки (здесь – Ni×Nj). Начальный момент первого порядка m1 называется математическим ожиданием или средним; начальный момент второго порядка m2 – средним квадрантом; моменты третьего и четвертого порядков используются для вычисления описанных ниже коэффициентов асимметрии и эксцесса. Отметим, что статистический анализ (вычисление моментов, формирование гистограмм и т.п.) может быть выполнен не только для изображения в целом, но и для любого заданного фрагмента. Существуют и более изощренные приемы. Так, в ряде случаев используется так называемый “анализ по маске”, когда обрабатываются элементы поля, образующие заданную маской конфигурацию. Анализ по маске позволяет определять статистические свойства отдельных объектов изображения, выделенных известными методами, а также произвольно заданных областей. Его программная реализация не встречает серьезных затруднений. Учитывая сказанное, перепишем выражение (4.2), не указывая явно границы суммирования:
где sum – количество обработанных пикселей исходного изображения. |
Билет 7
Статистические моменты в задаче оптимизации.
Билет 3
2.Модель постановки проблемы.
Моделирование представляет собой циклический процесс,т.е. за первым четырехэтапным циклом может последовать второй, третий и т.д. При этом знания об исследуемом объекте расширяются и уточняются, а первоначально построенная модель постепенно совершенствуется. Теперь перейдем к процессу экономико-математического моделирования, т.е. описания экономических и социальных систем и процессов в виде экономико-математических моделей. Выделим и рассмотрим подробно шесть этапов:
1.Постановка экономической проблемы и ее качественный анализ.
На этом этапе нужно сформулировать сущность проблемы, принимаемые предпосылки и допущения. Необходимо выделить важнейшие черты и свойства моделируемого объекта, изучить его структуру и взаимосвязь его элементов, хотя бы предварительно сформулировать гипотезы, объясняющие поведение и развитие объекта.
2.Построение математической модели.
Это этап формализации экономической проблемы, т.е выражения ее в виде конкретных математических зависимостей (функций, уравнений, неравенств и др.). Построение модели подразделяется на несколько стадий. Сначала определяется тип экономико-математической модели, изучаются возможности ее применения в данной задаче, уточняются конкретный перечень переменных и параметров и форма связей. Для некоторых сложных объектов целесообразно строить несколько разноаспектных моделей; при этом каждая модель выделяет лишь некоторые стороны объекта, а другие стороны учитываются приближенно. Оправдано стремление построить модель, относящуюся к хорошо изученному классу математических задач, что может потребовать некоторого упрощения исходных предпосылок модели, не искажающего основных черт моделируемого объекта. Однако возможна и такая ситуация, когда формализация приводит к неизвестной ранее математической структуре.
3. Математический анализ модели.
На этом этапе чисто математическими
приемами исследования выявляются общие свойства модели и ее решений. В
частности, важным моментом является доказательство существования решения
сформулированной задачи. При аналитическом исследовании выясняется,
единственно ли решение, какие переменные могут входить в решение, в
каких пределах они изменяются, каковы тенденции их изменения и т. д.
Однако модели сложных экономических объектов с большим трудом поддаются
аналитическому исследованию; в таких случаях переходят к численным
методам исследования.
4.Подготовка исходной информации.
В экономических задачах это, как правило, наиболее трудоемкий этап моделирования, так как дело не сводится к пассивному сбору данных. Математическое моделирование предъявляет жесткие требования к системе информации; при этом надо принимать во внимание не только принципиальную возможность подготовки информации требуемого качества, но и затраты на подготовку информационных массивов. В процессе подготовки информации используются методы теории вероятностей, теоретической и математической статистики для организации выборочных обследований, оценки достоверности данных и т.д. При системном экономико-математическом моделировании результаты функционирования одних моделей служат исходной информацией для других.]
5.Численное решение.
Этот этап включает разработку алгоритмов численного решения задачи, подготовку программ на ЭВМ и непосредственное проведение расчетов; при этом значительные трудности вызываются большой размерностью экономических задач. Обычно расчеты на основе экономико-математической модели носят многовариантный характер. Многочисленные модельные эксперименты, изучение поведения модели при различных условиях возможно проводить благодаря высокому быстродействию современных ЭВМ. Численное решение существенно дополняет результаты аналитического исследования, а для многих моделей являестя единственно возможным.

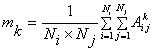 .
(4.2)
.
(4.2)