БИЛЕТ 1

1. Типы графов. Операции над графами. Подграфы.

1.Типы графов.

Граф G называется полным, если любые две его вершины смежны. Полный граф порядка n обозначается символом K_n, число ребер в нем равно, очевидно, n(n–1)/2. Граф называется пустым, если в нем нет ребер. Пустой граф порядка обозначается через O_n. простые циклы C_n (n = 3, 4) и простые цепи P_n (n = 2, 3, 4). граф Петерсена, который получается соединением двух простых циклов. колеса W_n (n = 3, 4, 5). Заметим, что W₃ = K₄ и | W_n | = n + 1. Граф называется двудольным, если существует такое разбиение множества его вершин на две части (доли), что концы каждого ребра принадлежат разным частям. Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным. Полный двудольный граф, доли которого состоят из p и из q вершин, обозначается символом K_p,q. При p = 1 получаем звезду K_1,q. Очевидно, что K_1,1 = K₂ = P₂, K_1,2 = P₃ и K_2,2 = C_4. Пусть G и H — графы, а  : VG  VH — взаимно однозначное отображение (биекция). Если для любых вершин и графа G их образы (u) и (v) смежны в H тогда и только тогда, когда u и v смежны в G, то эта биекция называется изоморфизмом графа G на граф H. Если такой изоморфизм существует, то мы пишем G  H (тогда и H  G) и говорим, что графы G и H изоморфны. Граф порядка называется помеченным, если его вершинам присвоены некоторые метки, например, номера 1, 2, …, n. Отождествив каждую из вершин графа с ее номером (и, следовательно, множество вершин — с множеством чисел {1, 2, …, n}, определим равенство помеченных графов G и H одного и того же порядка: G = H тогда, когда EG = EH. Для произвольного графа G следующим образом определяется дополнительный граф (или дополнение) 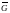: 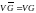, и любые две несовпадающие вершины смежны в тогда и только тогда, когда они не смежны в G.

2.Операции над графами

Дополнение ребра: G+e: пара не смежных вершин соединяется ребром.

Удаление ребра: G-e: пара смежных вершин становится не смежными.

Добавление вершины: G+v: новая вершина v соединяется с вершинами или появляется около вершин.

Удаление вершины: G-v:убирается вершина.

Отождествление вершин:

1. Удаляем вершину (u и v) из графа.

2. Добавляем вершину W соединяем с соседями

(G-u-v)+W

Стягивание ребра: отождествление смежных вершин.

Графы называются стягиваемыми, если они получаются друг из друга операцией стягивания ребер.

Подразбиение ребра:

1. Удалим ребро (u;v).

2. Добавим вершину W.

3. Соединим W c u и v.

Графы H и G – гомеоморфные, если они получаются из одного и того же графа операцией подразбиения ребер.

Дизъюнктное объединения графов

G(V,E) и H(X,Y), т.ч. V∩X = Ø

Граф G U H имеет множество вершин V и X и множество ребер E и Y

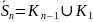
3.Подграфы

Граф H называется подграфом (или частью) графа G, если VH  VG и EH  EG. Если H — подграф графа G, то говорят, что H содержится в G. Подграф H называется остовным подграфом, если VH = VG. Если множество вершин подграфа H есть U, а множество его ребер совпадает с множеством всех ребер графа , оба конца которых принадлежат U, то H называется подграфом, порожденным (или индуцированным) множеством U, и обозначается через G(U). Важный класс подграфов составляют подграфы, полученные в результате удаления вершин. Пусть v — вершина графа G. Граф G_v = G – v получается из графа G в результате удаления вершины и всех инцидентных ей ребер.

Очевидно, что G_v = G (VG \ v). Подграф, множество вершин которого совпадает с множеством вершин всего графа, называется остовным подграфом (или суграфом).