5. Исследуем остаточную компоненту на адекватность условиям Гаусса-Маркова. Оценим точность модели.

Запишем условия Гаусса-Маркова:

1. , …, – случайные величины. Можно ли считать, что полученный ряд остатков , …, – значения случайной величины (проверка на случайность)?

2. - можно ли считать, что числа , …, – это результат измерения нормальной случайной величины?

3. , - можно ли считать, что , …, – это результаты измерения некоторой случайной величины с математическим ожиданием равным нулю?

4. Случайные величины , …, – независимы. Является ли ряд остатков , …, результатом независимых измерений, т.е. отсутствует ли в ряду , …, автокорреляция?

Если все 4 условия выполнены, то построенная модель считается адекватной.

Для решения построим таблицу, - остаточная компонента, для расчетов примем данные из пункта 4.

ti	Ei	Поворотные точки
1	0,365084		0,365084822	0,133286	0,048661	0,017765	-1,668336	2,950346
2	-1,30325	0	-1,303251325	1,698464	-2,21352	2,88478	-1,481422	2,194612
3	-2,78467	1	-2,784673622	7,754407	-21,59349	60,130830	2,3809581	5,668961909
4	-0,40371	1	-0,403715431	0,162986	-0,0658	0,0265644	-1,541932	2,377556991
5	-1,94564	1	-1,945648306	3,78554	-7,365343	14,330368	2,062197	4,2526587
6	0,116549	0	0,116549236	0,01358	0,001583	0,0001845	0,402343	0,161880375
7	0,518892	1	0,518892839	0,269249	0,139711	0,0724954	-0,724675	0,525154575
8	-0,20578	1	-0,205782658	0,042346	-0,008714	0,0017932	1,786367	3,191110243
9	1,580585	1	1,580585234	2,498249	3,9486965	6,2412514	-0,3939	0,155158868
10	1,186683	1	1,186683129	1,408216	1,671107	1,9830746	1,079076	1,16440538
11	2,265759	1	2,265759299	5,133665	11,63164	26,354518	-1,656242	2,743139276
12	0,609516		0,609516782	0,371510	0,226442	0,1380202
Среднее	-9,57831E-08			1,939292	-1,131585	9,3484705
Сумма		8		21,23151				28,53196

п. 1 условий Гаусса-Маркова:

Обозначим через – случайную величину, равную количеству поворотных точек в ряду , …, . Точка с номером называется поворотной если либо , . Установлено, что , .

Правило построения доверительного интервала с уровнем доверия .

1. Выбираем - 95%

2. Находим из равенства , решив получим 1, для заданного / ~ 1,026

3. Строим доверительный интервал:

В нашем случае: 6,67, 1,81.

5,29<= π_n(ω)<=8,05.

Вычисляем количество поворотных точек в ряду чисел , …, , в нашем случае π_n=8. Если π_n принадлежит доверительному интервалу, то ряд , …, признается случайным на уровне доверия . В противном случае ряд , …, является неслучайным.

Так как π_n=8 принадлежит доверительному интервалу, то ряд , …, признается случайным.

п. 2 условий Гаусса-Маркова:

Проверим ряд на соответствие нормальному распределению. Воспользуемся критерием асимметрии и эксцесса (для , ).

Вычислим выборочную асимметрию -0,419.

Теоретически установлено, что среднеквадратическая ошибка асимметрии равна:

0,555.

Доверительный интервал с уровнем доверия таков .

Правило проверки выборочной асимметрии на значимость:

Если , то признается незначимой, если , то значима, если , то данный критерий однозначного ответа дать не может.

В нашем случае

(0,419<0,8325) признается незначимой.

Вычислим выборочный эксцесс -0,51427.

Теоретически установлено, что среднеквадратическая ошибка асимметрии равна:

0,776.

Правило проверки на значимость выборочного эксцесса

Если , то эксцесс незначителен, если , то значим, если , то однозначного ответа нет.

В нашем случае (0,51427<1,164) признается незначимым.

Так как оба параметра незначительны, то можно продолжить дальше.

п. 3 условий Гаусса-Маркова:

Проверим гипотезу о равенстве нулю математического ожидания остаточной компоненты. Согласно критерию Стьюдента вычислим 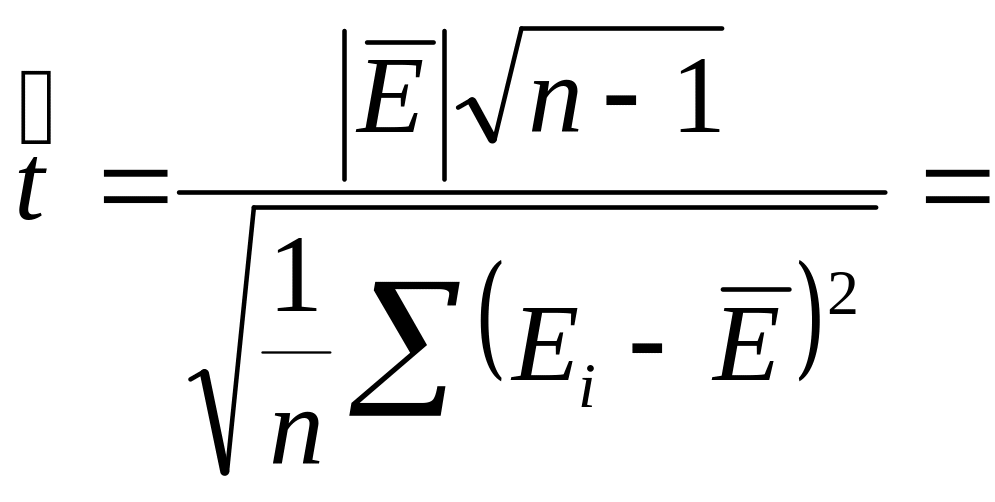-8,44692E-08

. По таблицам распределения Стьюдента с (12-1) – степенями свободы находим 1,7959. Сравниваем и : так ка , то на уровне значимости 0,95 принимается гипотеза о том, что математическое ожидание равно нулю.

п. 4 условий Гаусса-Маркова:

Исследуем остаточную компоненту на автокорреляцию. Воспользуемся критерием Дарбина-Уотсона.

Проверка гипотезы об отсутствии автокорреляции по критерию Дарбина-Уотсона

Зададим уровень доверия - 95%, что равно 0,95.

Вычисляем выборочное значение 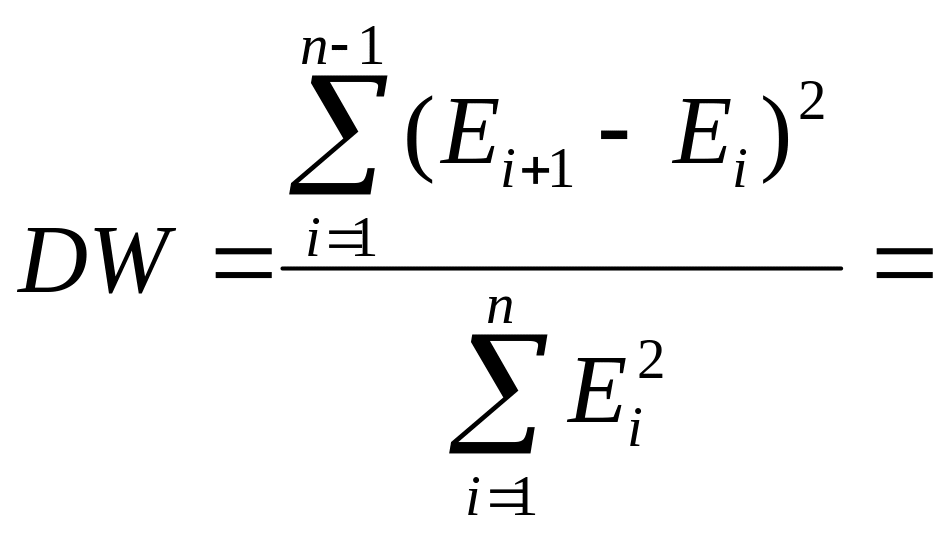1,34384952.

По таблицам находим и .

Согласно нашим данным 0,971, а 1,331.

Вычислим также 2,669 и 3,029.

Поскольку , принимаем гипотезу об отсутствии автокорреляции в ряду значений остаточной компоненты.

Проделав вычисления, видим, что все 4 условия Гаусса-Маркова выполнены, следовательно, остаточная компонента обладает необходимыми качествами, и модель является адекватной исходной постановке задачи.

Оценим точность построенной модели.

Абсолютная погрешность: 4,824.

Относительная погрешность (оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения): 4,8%.

Таким образом, модель, описывающая динамику изучаемого показателя, имеет вид (записать вид функции моделирующей данный динамический ряд ).

y(t)= 261,7493056-1,92141cos( πt/2) -5,22792 sin( πt/2)+ 1,4055611 cos(πt).