3. Используя аналитические методы выбрать модель тренда, построить модель и её график. Сравнить графики динамического ряда и модели тренда.
Тренд отсутствует.
4. Используя аналитические методы построить модель циклической компоненты. Сравнить графики динамического ряда и суммы модели тренда и модели циклической компоненты.
Построим сезонную
волну. В нашем случае сезонным периодом
является год. Значит, сезонных периодов
три и
.
В каждом сезонном периоде по 4 квартала,
значит
.
Общее количество наблюдений
.
Вычисляем
межпериодные средние
,
Здесь:
– i-ое наблюдение в j-ом периоде,
N – количество наблюдений в одном
периоде, в нашем случае
.
Полученные данные представим в таблице.
Год |
Квартал |
Месяц |
Среднее значение временного ряда |
Сезонная волна,
|
1995 |
1 |
1 |
255,4809 |
255,1158222 |
2 |
2 |
263,773033 |
265,0762778 |
|
3 |
3 |
262,787 |
265,5716667 |
|
4 |
4 |
260,829733 |
261,2334556 |
|
1996 |
1 |
5 |
253,170167 |
255,1158222 |
2 |
6 |
265,192833 |
265,0762778 |
|
3 |
7 |
266,090567 |
265,5716667 |
|
4 |
8 |
261,027667 |
261,2334556 |
|
1997 |
1 |
9 |
256,6964 |
255,1158222 |
2 |
10 |
266,262967 |
265,0762778 |
|
3 |
11 |
267,837433 |
265,5716667 |
|
4 |
12 |
261,842967 |
261,2334556 |
Строим
ломаные с узлами в точках (
;
)
и
(
;
),
где
первая ломаная является графиком
первоначального ряда за вычетом тренда,
а вторая –
графиком сезонной волны.
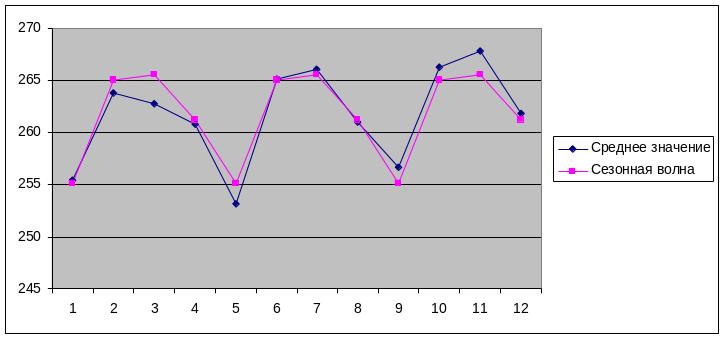
Визуальный анализ графиков исходных данных и сезонной волны показывает, что сезонная волна хорошо отражает колебания исходных данных и свидетельствует о наличии явно выраженной годичной периодичности данных.
Построим
циклическую компоненту
.
Для
разложения в ряд Фурье можно использовать
как исходные данные
,
так и точки сезонной
волны
.
Для сокращения
объёма вычислений воспользуемся точками
сезонной волны. Предварительный
вид циклической компоненты:
,
вычислим коэффициенты
частичной суммы ряда Фурье с учетом
того, что
,
,
.
В нашем случае
,
в развернутом виде:
V(t)= A0+ A1cos( πt/2)+ A2cos( πt)+ B1sin( πt/2)
Вычислим коэффициенты:
261,7493056; 
1,40556;
в нашем случае
-1,92141;
в нашем случае
-5,22792.
Предварительный вид циклической компоненты таков:
V(t)= A0+ A1cos( πt/2)+ A2cos( πt)+ B1sin( πt/2)= 261,7493056-1,92141 cos( πt/2) --5,22792 sin( πt/2)+ 1,4055611 cos( πt);
В разложении участвуют две элементарные гармоники:
V1 (t)= -1,92141 cos( πt/2) -5,22792 sin( πt/2) и V2 (t)= 1,4055611 cos( πt)
Для отбора значимых гармоник воспользуемся критерием Фишера.
Вычислим числа
,
.
В нашем случае
и
,
.
Здесь:
где n –
общее количество наблюдений в динамическом
ряду
.
-29,97796756.
Тогда
-1,932622843
и
-30,348185.
Выберем некий уровень доверия
,
где
,
и по таблицам распределения Фишера с
количеством степенной свободы (2;
),
в нашем
случае (2;7)
находим критическое число
19,35.
Так ка
и
обе гармоники являются значимыми и
остаются в функции циклической компоненты
.
Окончательно имеем:
V(t)= 261,7493056-1,92141 cos( πt/2) -5,22792 sin( πt/2)+ 1,4055611 cos( πt);
Год |
Квартал |
Месяц |
Среднее значение временного ряда |
Сезонная волна |
Циклическая компонента V(ti) |
1995 |
1 |
1 |
255,4809 |
255,1158222 |
255,1158 |
2 |
2 |
263,773033 |
265,0762778 |
265,0763 |
|
3 |
3 |
262,787 |
265,5716667 |
265,5717 |
|
4 |
4 |
260,829733 |
261,2334556 |
261,2334 |
|
1996 |
1 |
5 |
253,170167 |
255,1158222 |
255,1158 |
2 |
6 |
265,192833 |
265,0762778 |
265,0763 |
|
3 |
7 |
266,090567 |
265,5716667 |
265,5717 |
|
4 |
8 |
261,027667 |
261,2334556 |
261,2334 |
|
1997 |
1 |
9 |
256,6964 |
255,1158222 |
255,1158 |
2 |
10 |
266,262967 |
265,0762778 |
265,0763 |
|
3 |
11 |
267,837433 |
265,5716667 |
265,5717 |
|
4 |
12 |
261,842967 |
261,2334556 |
261,2334 |
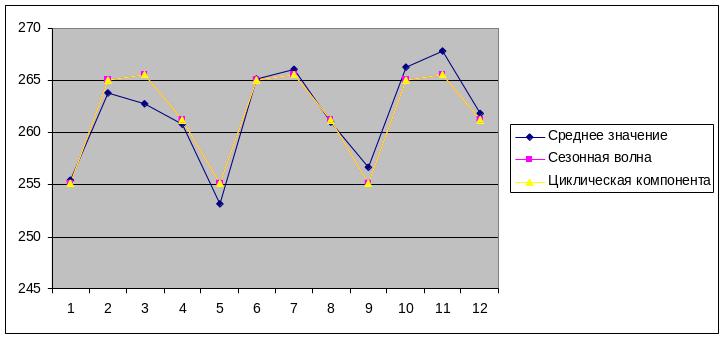
Графики динамического ряда (было взято среднее значение), модель тренда – она отсутствует и модели циклической компоненты.
