41.Формула полной вероятности.

П усть событие А может наступить при условии реализации одной из гипотез Н₁, Н₂, ..., Н_n, образующих полную группу событий.

Т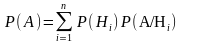 огда

. (1)

Формула (1) называется формулой полной вероятности.

42. Теорема Байеса

Теорема Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность наступления события в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях. Иначе, по формуле Байеса можно более точно пересчитывать вероятность, беря в учет как ранее известную информацию, так и данные новых наблюдений.

• П редположим, что в результате испытания событие А произошло. Какова вероятность, что событие А произошло в результате реализации гипотезы Н_k , т.е. P(H_k/A) = ? (происходит переоценка вероятностей гипотез). Ответ дает формула Байеса:

или

 — априорная вероятность гипотезы A;

 — вероятность гипотезы A при наступлении события B (апостериорная вероятность);

 — вероятность наступления события B при истинности гипотезы A;

 — вероятность наступления события B.

 — математическая формула априорной вероятности наступления события B , где суммирование идет по всем гипотезам Ai;

43. Формула Бернулли

Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний.

Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность P_k,n того, что событие A наступит k раз в n независимых испытаниях, равна:   где q = 1-p.

44.Случайные величины. Способы их описания.

Дисперсией D(X) случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания:

D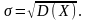 (X) = M[Х-M(X)]² или D(X) = M[X-a]² , где а = М(Х). Часто вместо дисперсии используют среднее квадратическое отклонение:

Свойства дисперсии случайной величины.

1. Дисперсия постоянной величины равна нулю: D(С) = 0.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его и квадрат : D(кХ) = к²D(X)

3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом математического ожидания D(X) = М(Х²)-[М(Х)]².

Функция распределения случайной величины

Пусть дана функция F(x) определённая следующим образом: для каждого х значение F(x) равно вероятности того, что дискретная величина X примет значение, меньшее х, F(x) = Р(Х<х). Эта функция называется интегральной функцией распределения.

Функция распределения  самая универсальная характеристика случайной величины.

Ее свойства:

1. Функция распределения  неубывающая функция. F(x₂) ≥F(x₁), если х₂>x₁.

2. 0 ≤ F(x) ≤ 1.

3. Вероятность того, что случайная величина X лежит в пределах

х₁ < X < х₂ , т.е. P(х₁ < X < х₂) вычисляется как Р(х₁ < Х < х₂) = F(x₂) ─ F(x₁).

График функции распределения представляет собой график возрастающей функции, значения которой начинаются с 0 и кончаются 1.