1.Графики и свойства основных элементарных функций.

Свойства:

1.Четность и нечетность. Функция у = f(х) называется четной, если для любых значений х из область определения f(х)= f(х) и нечетной, если f(х) =  f(х). В противном случае функция у = f(х) называется функцией общего вида.

Например, функция у = х, является нечетной, так как f(х) =  х = f(х).

График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

2.Монотонность. Функция у = f(х) называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

Функции возрастающие и убывающие называются строго монотонными функциями.

Например, функция у = х, является возрастающей для всех хR.

3.Ограниченность. Функция у = f(х) называется ограниченной на промежутке Х, если существует такое положительное число М, что  f(х)  М для любого х Х.

Например, функция у = sin х ограниченна на всей числовой оси, т.к.  sin х   1 для любого хR.

4.Периодичность. Функция у = f(х) называется периодической с периодом Т  0, если для любых х из области определения функции f(х+Т) = f(х).

Например, функция у = sin х имеет наименьший положительный период Т = 2, так как для любых х sin (х+2) = sin х.

Основными элементарными функциями называются следующие функции:

степенная у = хⁿ, где nN;

показательная у = а^х, где а > 0, а  1;

логарифмическая у = log_ax ,где а > 0, а  1;

тригонометрические: у = sin x, y = cos x, y = tg x, y = ctg x.

Степенная функция у = хn, nN и её свойства ООФ -область определения функции; ОЗФ – область значения функции. a) n- нечетное число (y=x; y=x3) 1.ООФ - x (-∞ ,+∞ ) 2.ОЗФ - y (-∞ ,+∞ ) 3. нечетная : y(-x)=-x=-y(x) 4.монотонность: возрастает на (-∞ ,+∞ ) 5. не периодическая

b) n- четное число (y=x2) 1.ООФ - x (-∞ ,+∞ ) 2.ОЗФ - y (0 ,+∞ ) 3. четная : y(-x)=(-x)2=x2=y(x) 4.убывает: (-∞ ,0 ); возрастает на (0 ,+∞ ) 5. не периодическая Степенная функция у = х-n, nN и её св-ва a) n- нечетное число (y=1/x ) 1.ООФ - x  (-∞ ,0 )U (0 ,+∞ ) 2.ОЗФ - y  (-∞ ,0 )

3. нечетная : y(-x)=-1/x=-y(x) 4.монотонность: убывает на (-∞ ,0 )U(0 ,+∞ ) 5. не периодическая b) n- четное число (y=1/x2) 1.ООФ - x  (-∞ ,0 )U (0 ,+∞ ) 2.ОЗФ - y (0 ,+∞ ) 3. четная : y(-x)=(-x)2=x2=y(x) 4.убывает: (0, +∞ ); возрастает на (-∞,0 ) 5. не периодическая

2.Предел функции

Предел функции в точке

• Число А называется пределом функции у = f(х) при х, стремящимся к х₀, если для любого, даже сколь угодно малого положительного числа , найдется такое положительное число  ( зависящее от ), что для всех х , не равных х₀ и удовлетворяющих условию

•  х- х₀   ,

• верно неравенство:

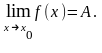
•  f(x)– А   

• Этот предел функции обозначается:

Предел функции в бесконечности

• Число А называется пределом функции у = f (х) при х, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа , найдется такое положительное число S ( зависящее от ), что для всех х таких, что х  S, верно

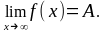• неравенство: f(x)–А

• Этот предел функции обозначается: