- •Предмет физики. Методы физический исследований: опыт, гипотеза, эксперимент, теория.
- •Предмет механики. Кинематика и динамика. Основные единицы международной системы единиц механики(си).
- •Физические модели: материальная точка, системы материальных точек, абсолютно твёрдое тело, сплошная среда(кинематика).
- •Три способа кинематического описания движения материальной точки: векторный, координатный и естественный способ задания движения точки.
- •Скорость и ускорение материальной точки. Виды и характер движения точки.
- •Кинематика абсолютно твёрдого тела: простейшие виды движения тела, взаимосвязь между линейными и угловыми характеристиками при вращательном движении.
- •Сложное движение: динамика.
- •Основная задача динамики: прямая и обратная задача динамики.
- •Важнейшие понятия динамики материальной точки: инертность, масса, импульс, масса, сила.
- •Меры действия силы и динамические меры механического движения: момент силы, работа и мощность силы, момент импульса. Кинетическая энергия.
- •Законы изменения момента импульса и кинетической энергии материальной точки. Уравнение моментов, взаимосвязь между изменением кинетической энергии материальной точки и работой сил.
- •Явление трения скольжения, качения и вязкого сопротивления: внешнее и внутреннее трение. Трение покоя и трение скольжения. Трение качения. Вязкое трение.
- •Сила упругости. Закон Гука: виды деформации тела.
- •Закон всемирного тяготения. Энергия. Закон сохранения энергии в механике.
- •Потенциальная энергия консервативных сил: потенциальная энергия и её связь с работой консервативных сил.
- •Абсолютно упругий/неупругий центральный удар.
- •Взаимосвязь между потенциальной энергией и силой взаимодействия: сила – градиент потенциальной энергии. Понятия потенциальной ямы и потенциального барьера.
- •Потенциальное поле. Характеристики и свойства гравитационного поля. Принцип суперпозиции полей.
- •Неинерциальная система отсчёта: силы инерции, второй закон ньютона в неинерциальной системе, динамика абсолютно твёрдого тела.
- •29. Гармонический осциллятор. Примеры: Пружинный, математический, физический маятники.
- •30. Представление колебаний в виде векторов.
- •31. Сложение колебаний одного направления и перпендикулярных колебаний.
- •32. Свободные затухающие колебания и их характеристики. Затухание свободных колебаний
- •33. Вынужденные колебания. Резонансные кривые.
- •34. Распространение волн в упругой среде. Продольные и поперечные волны
- •35. Уравнение бегущей волны. Фазовая и групповая скорости.
- •36. Энергетические характеристики волны. Плотность потока энергии волны.
- •37. Стоячие волны. Эффект Доплера.
- •38. При́нцип относи́тельности Эйнштеина. Инвариантность скорости света
- •39. Замедление времени и сокращение длин
- •40. Преобразования Лоренса в сто
- •43 Общие свойства жидкостей и газов
- •44 Уравнение неразрывности
- •45 Уравнение Бернулли
- •46 Вязкость. Ламинарные и турбулентные режимы течения
- •47. Термодинамический и статистический методы
- •48. Изопроцессы идеального газа
- •49. Основное уравнение молекулярно-кинетической теории идеальных газов. Молекулярно-кинетический смысл температуры
- •52 Теплоемкость. Классическая теплоемкость идеального газа и ее недостатки
Предмет физики. Методы физический исследований: опыт, гипотеза, эксперимент, теория.
В переводе с греческого «физика» - наука о природе.
Опыт - основной метод исследования в физике.
Опыт - это наблюдение исследуемого явления в точно контролируемых условиях,
позволяющих следить за ходом явления и воссоздать его каждый раз при повторении этих
условий.
Гипотеза - научное предположение, выдвигаемое для объяснения какого-либо факта или
явления. Гипотеза подтверждается опытом.
Эксперимент - научно поставленный опыт с целью проверки гипотезы.
Физическая теория - система основных идей, обобщающих опытные данные и
отражающих объективные закономерности природы.
Физическая теория дает объяснение целой области явлений природы с единой точки зрения.
Предмет механики. Кинематика и динамика. Основные единицы международной системы единиц механики(си).
Механика - часть физики, изучающая закономерности механического движения. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564 - 1642) и окончательно сформулированы английским ученым И. Ньютоном (1643 - 1727).
Механика Галилея-Ньютона называется классической механикой, в ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме (V<<с). Законы движения макроскопических тел со скоростями, сравнимыми со скоростью света в вакууме, изучаются релятивистской механикой, законы движения микроскопических тел (отдельные атомы и элементарные частицы) - изучаются квантовой механикой.
Механика делится на три раздела: кинематику, динамику, статику.
Кинематика изучает движение тел, не выясняя причин, его обуславливающих.
Динамика изучает законы движения тел и причины, обуславливающие это движение.
Статика изучает законы равновесия системы тел. Если известны законы движения тел, то из них можно установить и законы равновесия. Поэтому физика отдельно от законов динамики законы статики не рассматривает.
Физические модели: материальная точка, системы материальных точек, абсолютно твёрдое тело, сплошная среда(кинематика).
Механика для описания движе ния тел в зависимости от условий конкретных задач использует разные физические модели. Простейшими моделями являются материальная точка - МТ и абсолютно твердое тело - АТТ.
Материальная точка (МТ) - тело, размерами которого можно пренебречь по сравнению с
расстояниями до других тел.
Абсолютное твердое тело (АТТ) - тело, деформациями которого в условиях данной задачи
можно пренебречь.
Система материальных точек – совокупность материальных точек, объединяемых общими законами взаимодействия.
Сплошна́я среда́ — механическая система, обладающая бесконечным числом внутренних степеней свободы.
Три способа кинематического описания движения материальной точки: векторный, координатный и естественный способ задания движения точки.
Векторный способ. Положение точки можно задать, как известно, и с помощью радиус-вектора. При движении материальной точки радиус-вектор, определяющий ее положение, с течением времени изменяется (поворачивается и меняет длину; рис.1.8), т. е. является функцией времени:
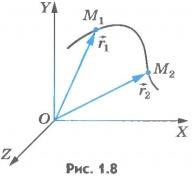
Координатный способ. Будем задавать положение точки с помощью координат (рис.1.7). Если точка движется, то ее координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени.

Математически это принято записывать в виде