2. Плотность распределения нормального закона. Вероятность попадания случайной величины с нормальным законом распределения на заданный интервал

Найти дисперсию случайной величины с нормальным законом распределения.

Решение. Для случайной величины с нормальным законом распределения плотность вероятностей имеет вид

f(x) =

Поэтому с учетом формулы для дисперсии имеем

DX = (x-MX)²f(x)dx = = = = , т.е. DX = .

3. Свойства функции Лапласа. Правило трех сигм.

Функция Лапласа обладает следующими свойствами:

1) Ф(0) = 0;

2) Ф(-х) = - Ф(х);

3) Ф(¥) = 1.

Оценим с помощью центральной предельной теоремы 4.4.1 вероятность того, что частота отличается от вероятности успеха в испытаниях Бернулли по модулю меньше (или не меньше) чем на произвольное . Имеем

где 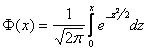– функция Лапласа.

Таким образом имеем . С другой стороны, .

Пример 2. Среднее арифметическое. Пусть X₁, X₂, ... попарно независимые случайные величины, . Закон больших чисел в форме теоремы Чебышева (4.2.4) имеет вид , при .

Если , ... не только попарно независимы, но и независимы в совокупности, можно применить теорему 4.4.1. Это дает: ^{Поэтому имеем} , (4.4.8)

Из табл. 4 для функции Лапласа Ф(х) следует, что при =3, т.е. при вероятность

Это так называемое правило 3 (трех сигм). Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратичного отклонения. В этом и состоит сущность правила «трех сигм».

4. Локальная теорема Муавра-Лапласа.

Пусть вероятность "успеха" р в каждом из n испытаний Бернулли постоянна и отлична от 0 и 1. Тогда имеет место следующая приближенная формула (которая тем точнее, чем больше n):

, где , .

5. Интегральная теорема Муавра-Лапласа.

Пусть m – число "успехов" в серии из n независимых испытаний, p – вероятность "успеха" в каждом испытании, 0<р<1, ,b R, <b. Тогда: ,

причем стремление к пределу равномерно относительно a и b, ‑∞ <   < b < +∞.

Практическое применение интегральной теоремы Муавра-Лапласа основано на приближенной формуле: . Формула обеспечивает хорошую точность уже при значениях npq10.

6. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях.

7. Простейший поток событий.

Пусть некоторое случайное событие А (называемое в дальнейшем “успехом”) может происходить случайным образом в течение времени t. Свяжем с этим потоком событий случайную величину X(t), являющуюся числом наступления “успехов” в течение времени t. Пусть этот поток событий обладает следующими свойствами.

1. Отсутствие последействия. Для любых непересекающихся интервалов времени длиной t₁, t₂, …, t_k случайные величины X(t₁), X(t₂), …,X(t_k) являются независимыми.

2. Стационарность. Случайная величина X(t) зависит лишь от величины t интервала и не зависит от его начала, поэтому интервал может быть взят с началом в точке t = 0.

3. Ординарность. Для любых малых промежутков времени Δt имеет место равенство

P(X(Δt) = 1) = λΔt + o(Δt), λ>0,

где λ – интенсивность потока случайных событий.

Свойство ординарности означает, что для малых промежутков времени Δt “успех” может наступить лишь один раз (или не наступить вообще), а вероятность наступления “успеха” большее число раз является бесконечно малой величиной большего порядка чем Δt.

Поток случайных событий, обладающий свойствами отсутствия последействия, стационарности и ординарности, называется пуассоновским (простейшим) потоком случайных событий.