- •Понятие функции. Графики функций.
- •Действительные числа. Метод математической индукции. Абсолютная величина.
- •Предел последовательности.
- •Вычисление предела последовательности.
- •Предел функции.
- •Решение: возьмем
- •Вычисление предела функции.
- •Непрерывность и точки разрыва функции.
- •Дифференциал и дифференцируемость функции.
- •Производные высших порядков, ряд Тейлора.
- •Правило Лопиталя и его применение к нахождению предела функции.
- •Неопределенность . По правилу Лопиталя данный предел равен
Дифференциал и дифференцируемость функции.
Опр.1. Функция y=f(x): v(x0)R называется дифференцируемой в точке х0 , если ее приращение в этой точке y=f(x0+x)-f(x0).
x=x-x0, представимо в виде:
y=A x+(x)x, (1)
где А- некоторая const, не зависящая от x , а (х)0 при х0.
Опр.2. Главная линейная часть приращения функции относительно х называется дифференциалом функции f в точке х0 и обозначается df(x0) или, короче, dy=Ax. Таким образом,
y=dy+0(x) при х0 (2).
Т.к.
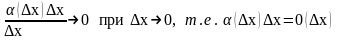
Для большей симметрии записи дифференциала приращение х обозначают dх и и называют его дифференциалом независимого переменного. Таким образом, dy=Adx.
Пример 1. Доказать, что функция y=x2-x+3 диффенцируема
на R.
Решение: возьмем хR, дадим ей приращение х, тогда
у=f(x+x)-f(x)=(x+x)2-(x+x)+3-(x2-x+3)=x2+2xx+(x)2-x-x+3-x2+x-3= (2x-1)x+(x)2
где
(х)2=0(х),
т.к.
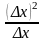 =х0
при х0.
=х0
при х0.
Т.о. у=Ах+0(х), где А=2х-1, т.е. у представимо в виде (1) в хR.
Теорема: Для того, чтобы функция y=f(x):U(x0)R была дифференцируемой в точке х0 она имела производную в х0, при этом dy=f /(x0)dx.
Пример 2. Доказать, что функция не дифференцируема в точке =0.
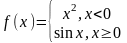
Решение: Имеем
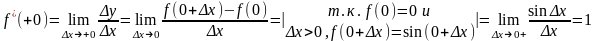
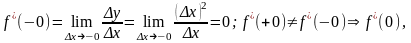
т.е. в точке =0 не дифференцируема.
Пример 3. Пользуясь понятием дифференциала, найти приближенное значение
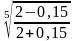
Решение:
рассмотрим функцию
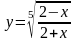 ,тогда
,тогда
- есть значение данной функции при х=0,15
Пусть х0=0, х=0,15. Тогда у(0)=1.
Из (2) видно, что y=dy, a dy=f /x ,т.е.
yf /(x)x, y=f(x+x)-f(x) .
Отсюда f(x+x)f(x)+f /(x)x . В нашем. случае x=0,
x+x=0,15; f(0,15)f(0)+f /(0) 0,15.
Определим
Производные высших порядков, ряд Тейлора.
Если
функция f:ХR,
xR,дифференцируема
в xX,то
на множестве X
возникает функция f
:XR,значение
которой в точке xX
равно производной f
(x).Если
же функция f
:XR
имеет производную (f
):XR
на множестве x,то
(f
)(x)
называется второй производной функции
f(x)
и обозначается f
(x)
или
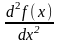 .
Если f
(x)
имеет производную (f
(x)),то
эта производная называется третьей
производной функции f(x)
или производной третьего порядка функции
f(x)
и обозначаются одним из символов f
(x),
f
(3)(x),
.
Если f
(x)
имеет производную (f
(x)),то
эта производная называется третьей
производной функции f(x)
или производной третьего порядка функции
f(x)
и обозначаются одним из символов f
(x),
f
(3)(x),
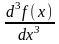
Производная n-го порядка является производной от производной
(n-1) порядка, т.е.
f (n)=(f (n-1))/ (x)
Производные,
начиная со второй, называются производными
высших порядков и обозначаются
у//,у///,у(4),…у(n),
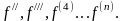
Производные n-го порядка некоторых элементарных функций:
( x)(n)= xlnnx (
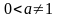 )
)(sinx)(n)=
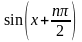
(xm)(n)=m(m-1)…(m-n+1)xm-n
(ex)(n)=ex
(cosx)(n)=
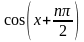
(lnx)(n)=
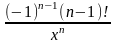
Если функции u=(x) и v=(x) имеют производные n-го порядка (n- кратно дифференцируемы),
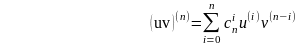 (1)
(1)
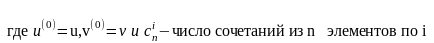
Пример 1: Вычислить n-ю производную (n2) функции y=x2cosx .
Решение: полагая u=cosx и v=x2, найдем
u(n)=cos(x+nπ/2), v'=2x, v''=2,v''''=v(4)=…=0.
Подставляя в формулу (1), получаем
y(n)=c0ncos(x+nπ /2)x2+c1ncos(x+(n-1) π/2)2x+c2ncos(x+(n-2) π/2)2
Формула (1) называется формулой Лейбница.
Опр. Функция у называется заданной параметрически, если зависимость между у и х задана системой уравнений
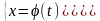 ,tT
,tT
П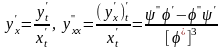 роизводные
этой функции могут быть найдены по
формулам:
роизводные
этой функции могут быть найдены по
формулам:
Пример
2. Найти
производные
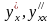 от функции
y=y(x)
, заданной параметрически если x=acost,
y=asint
от функции
y=y(x)
, заданной параметрически если x=acost,
y=asint
Решение:
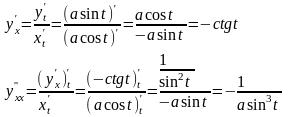
Формула Тейлора. Пусть функция f(x) имеет в точке а и некоторой ее окрестности производные порядка n+1. Пусть х-любое значение аргумента из указанной окрестности, х=а. Тогда между точками а и х найдется точка такая, что справедлива следующая формула:
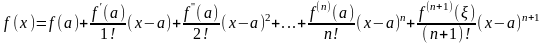 Частный,
простейший вид формулы Тейлора при а=0
принято называть формулой Маклорена:
Частный,
простейший вид формулы Тейлора при а=0
принято называть формулой Маклорена:
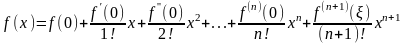
Пример 3. Разложить в ряд Тейлора функции у=1/х при а=-2.
Решение: вычисляем значения данной функции и ее производных при х=а=-2
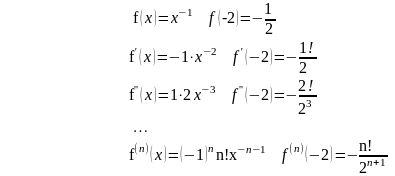
Подставляя эти значения в формулу Тейлора для произвольной функции, получим