- •Понятие функции. Графики функций.
- •Действительные числа. Метод математической индукции. Абсолютная величина.
- •Предел последовательности.
- •Вычисление предела последовательности.
- •Предел функции.
- •Решение: возьмем
- •Вычисление предела функции.
- •Непрерывность и точки разрыва функции.
- •Дифференциал и дифференцируемость функции.
- •Производные высших порядков, ряд Тейлора.
- •Правило Лопиталя и его применение к нахождению предела функции.
- •Неопределенность . По правилу Лопиталя данный предел равен
Решение: возьмем

Тогда соответствующие последовательности значений функции таковы:
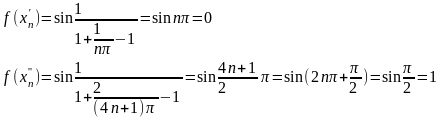
Следовательно,
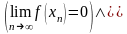 ,
т.е.
,
т.е.
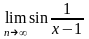 не существует
не существует
Замечание
2: Пример 2
показывает, что вывод о наличии предела
функции нельзя делать, исходя из
последовательности {xn}
частного вида (например, исходя из xn''
=1+ ),
а нужно рассматривать произвольную
последовательность {xn
}, имеющую заданный
),
а нужно рассматривать произвольную
последовательность {xn
}, имеющую заданный
предел а.
Пример 3: Пользуясь " – " определением предела, доказать, что
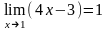
Р ешение: Надо доказать, что для >0 существует такое >0, что из неравенства 0 < |x-1| < следует, что |f(x)-1| < , f(x)=4x-3. Зададим
> 0 и рассмотрим выражение: |f (x)-1|=|4x-3-1|= 4|x-1|.
Если взять ≤ /4, то для всех х, удовлетворяющих неравенству |x-1| < , будем иметь |f(x)-1| = 4|x-1|<4 ≤ 4/4=.
Следовательно,
Пример
4: f(x)=1/(x-1)
доказать, что
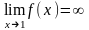
Решение:
По определению
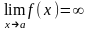 ,
если для
М>0 можно подобрать М>0,
что для всех ха,
удовлетворяющих неравенству
,
если для
М>0 можно подобрать М>0,
что для всех ха,
удовлетворяющих неравенству
0<|x-a|<,
будет выполняться условие
 >M.
В нашем случае по заданному M>0
будем подбирать М
из условия
>M.
В нашем случае по заданному M>0
будем подбирать М
из условия
|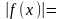 1/|x-1|>M
|x-1|<1/M.
1/|x-1|>M
|x-1|<1/M.
Следовательно,
положив M=1/М,
получим, что для всех х,
удовлетворяющих неравенству 0<|x-1|<M,
выполняется неравенство
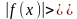 M,
значит,
M,
значит,
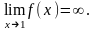
Вычисление предела функции.
При вычислении предела функции необходимо знать следующие
теоремы:

Кроме того, надо пользоваться тем, что для всех основных элементарных функций в любой точке их области определения справедливо равенство:
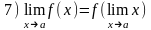 (в
силу непрерывности, Л.р. №7)
(в
силу непрерывности, Л.р. №7)
Этими простейшими пределами можно пользоваться как формулами:
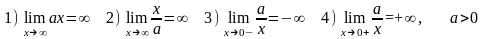

Более
сложные случаи нахождения предела
функции:
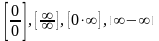 ,[1]
рассматриваются далее в отдельности.
,[1]
рассматриваются далее в отдельности.
Пример 1.Найти предел:
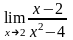
Решение:
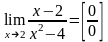
Разлагаем знаменатель на множители:

Здесь нет сокращения на нуль, что никогда недопустимо. Согласно определению предела функции аргумент х стремиться к своему предельному значению 2, никогда с ним не совпадая.
Пример 2. Найти предел:

Решение:
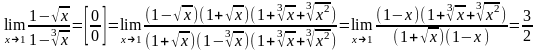 Пример
3.
Найти предел:
Пример
3.
Найти предел:
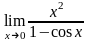
Решение:
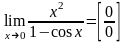
(Применяем тригонометрическую формулу так, чтобы использовать первый замечательный предел).
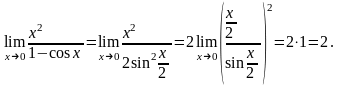
Пример 4. Найти предел:
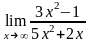
Решение:
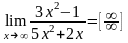
Деля числитель и знаменатель на наивысшую степень х (на х2), находим
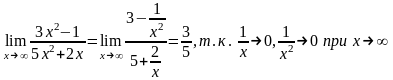
Случай,
когда при ха
или х
функция f(x)
представляет произведение бесконечно
малой величины на бесконечно большую
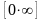 ,
приводится путем преобразования функции
к одному из двух рассмотренных случаев,
т.е. к
,
приводится путем преобразования функции
к одному из двух рассмотренных случаев,
т.е. к
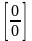 или к
.
или к
.
Случай,
когда при ха
или х
функция f(x)
представляет разность двух положительных
бесконечно больших величин
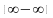 ,
можно привести к случаю
или
путем преобразования функции к дроби.
,
можно привести к случаю
или
путем преобразования функции к дроби.
Пример 5. Найти следующий предел:

Решение:
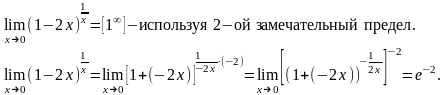
Непрерывность и точки разрыва функции.
Если
ищется предел функции
при условии, что аргумент
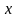 ,
стремясь к своему предельному значению
а,
может принимать только такие значения,
которые меньше а,
то этот предел, если он существует,
называется левосторонним
(левым) пределом данной функции в точке
=а
и условно обозначается так:
,
стремясь к своему предельному значению
а,
может принимать только такие значения,
которые меньше а,
то этот предел, если он существует,
называется левосторонним
(левым) пределом данной функции в точке
=а
и условно обозначается так:
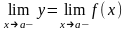 =
=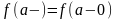
Аналогично можно сформулировать определение правостороннего (правого) предела данной функции, который обозначается так:
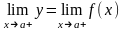 =
=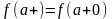
Теорема. Функция непрерывна при =а тогда и только тогда, когда:
1) функция определена не только в точке , но и в некотором интервале, содержащем эту точку;
2)функция имеет при а конечные и равные между собой односторонние пределы;
3)односторонние пределы при а совпадают со значением функции в точке а, т.е.
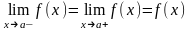
Если для данной функции в данной точке =а хотя бы одно из перечисленных трех условий не выполняются, то функция называется разрывной в точке =а.
Локальные свойства. Локальными называют такие свойства функций, которые определяются поведением функции в сколь угодно малой окрестности точки области определения.
Теорема.
Пусть
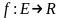 –функция,
непрерывная в точке а.
Тогда справедливы следующие утверждения:
–функция,
непрерывная в точке а.
Тогда справедливы следующие утверждения:
10
Функция
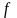 ограничена в некоторой окрестности
ограничена в некоторой окрестности
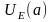 точки а.
точки а.
20
Если
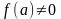 ,то в некоторой
окрестности
точки а
все значения функции положительны или
отрицательны вместе с
,то в некоторой
окрестности
точки а
все значения функции положительны или
отрицательны вместе с
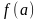 .
.
30
Если функция
 определена в некоторой окрестности
точки а и,как
и
,
непрерывна
в самой точке а,то
функции:
определена в некоторой окрестности
точки а и,как
и
,
непрерывна
в самой точке а,то
функции:
a)
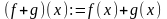 ,
,
b)
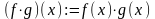 ,
,
c)
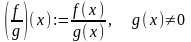 ,
определены
в некоторой окрестности точки
а и непрерывны
в точке а.
,
определены
в некоторой окрестности точки
а и непрерывны
в точке а.
40
Если функция
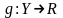 непрерывна в точке b,
а функция
непрерывна в точке b,
а функция
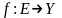 такова что
такова что
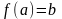 и
непрерывна
в точке а ,то
композиция
и
непрерывна
в точке а ,то
композиция
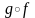 определена на
определена на
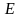 и также непрерывна в точке а.
и также непрерывна в точке а.
Опр.1.
Если точка
разрыва
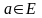 функции
такова , что
существуют конечные и равные
функции
такова , что
существуют конечные и равные
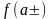 ,
но
,
но
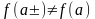 ,
то
,
то
 называется точкой устранимого разрыва
функции
.
называется точкой устранимого разрыва
функции
.
Опр.2. Разрыв функции в точке =а называется разрывом первого рода, если односторонние пределы слева и справа существуют, но не равны между собой. Если хотя бы один из односторонних пределов не существует или равен ∞, разрыв в этой точке называется разрывом второго рода.
Опр.3. Скачком функции в точке разрыва называется абсолютная величина разности между ее правым и левым предельными значениями.
Пример 1.Функция задана различными аналитическими выражениями для различных областей изменения аргумента х. Найти точки разрыва функции, если они существуют.
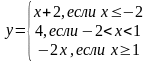
Решение:
Данная функция определена и непрерывна в интервалах
(-,2), (-2,1), (1,+),т.к. постоянная и непрерывная функции непрерывны на всей действительной оси . При х=-2 и х=1 меняется аналитическое выражение функции, и только в этих точках функция может иметь разрыв. Определим односторонние пределы в точке х=-2:
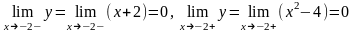
Односторонние пределы совпадают и равны значению функции в точке х=-2. Функция в этой точке непрерывна.
Определим односторонние пределы в точке х=1:
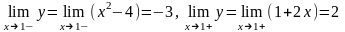
Т.к. односторонние пределы функции у=f(x) в точке х=1 не равны между собой, то в этой точке функция имеет разрыв первого рода. В точке х=1 скачок функции имеет значение, равное =|2-(-3)|=5. График функции показан на рис.1.
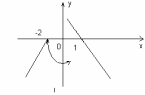 рис.1.
рис.1.
Пример
2. Дана функция
 .
Найти точки разрыва функции, если они
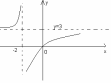
существуют. Построить график функции.
.
Найти точки разрыва функции, если они
существуют. Построить график функции.
Решение:
Наша функция является отношение 2-х линейных функций, которое является непрерывным на всей действительной оси. Значит, исходная функция непрерывна всюду на действительной оси, кроме () x=2.
При х=-2 данная функция не существует; в этой точке функция терпит разрыв. Определим односторонние пределы функции при х-2 слева и справа:
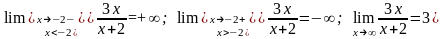
Таким образом, при х=-2 данная функция имеет разрыв второго рода.
Производная.
Опр.1.
Производной функции
по аргументу
называется предел отношения приращения
функции в точке
к приращению аргумента при условии, что
это последнее стремиться к нулю.
Производная функции
обозначается
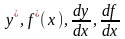 .
.
Таким образом, по определению
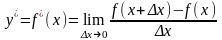 ,
x,
x+∆x
Df.
,
x,
x+∆x
Df.
Операция
отыскания производной
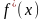 данной функции
называется дифференцированием этой
функции.
данной функции
называется дифференцированием этой
функции.
Геометрически число представляет собой угловой коэффициент касательной к графику функции в точке .
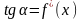
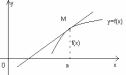
Пример 1. Исходя из определения производной, непосредственно найти производную функции у=х2.
Решение:
Придадим х приращение х и найдем приращение функции:
у=у(х+х)-у(х)=(х+х)2-х2=х2+2хх+(х)2-х2=2хх+(х)2

Основные правила нахождения производной.
Если с - постоянная величина и функции u=u(x), v=v(x), w=w(x)
имеют производные, то
(с)/=0
(cu)/=cu/
(u+v-w)/=u/+v/+w/
(uv)/=u/v+uv/
5)
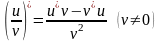
6)
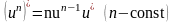
7)
если функции
 и
и
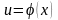 имеют производные, то yx/
=yu/
ux/
.
имеют производные, то yx/
=yu/
ux/
.
Пример 2.Вычислить производную функции: y=(2x2 –5x+1)ex
Решение:
y/ =(2x2 –5x+1)/ ex +(2x2 –5x+1)(ex )/ =(по правилу 4)=[(2x2 )/ –(5x)/ +1/]ex +(2x2 –5x+1)ex =
=(по правилу 3)=(4x-5)ex +(2x2 –5x+1)ex .
Если х- независимая переменная, то
Основные формулы.
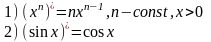
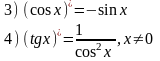

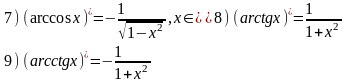
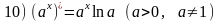

Пример
3. Вычислить
производную функции:
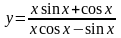
Решение:
Воспользуемся сначала правилом 5), а затем правилами 3) и 4) и формулами 2) и 3).