Введение в анализ

1. Множество - это совокупность, набор элементов, объединенных общими свойствами.

Множества обозначаются заглавными латинскими буквами , а элементы множества строчными латинскими буквами .

Запись означает, что есть множество с элементами , которые связаны между собой какой-то функцией .

Замечание. Элементы в множество входят по одному разу, т.е. без повторений.

Основные операции:

1. Принадлежность элемента множеству:

где -- элемент и -- множество (элемент принадлежит множеству  ).

2. Непринадлежность элемента множеству:

где -- элемент и -- множество (элемент не принадлежит множеству  ).

3. Объединение множеств: .

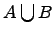Объединением двух множеств и называется множество , которое состоит из элементов множеств и , т.е.

   или

4. Пересечение множеств: .

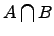Пересечением двух множеств и называется множество , которое состоит из общих элементов множеств и , т.е.

   и

5. Разность множеств: .

Разностью двух множеств и , например, множество минус множество , называется множество , которое состоит из элементов множества , которых нет в множестве , т.е.

   и

6. Симметрическая разность множеств: .

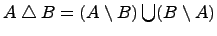Симметрической разностью двух множеств и называется множество , которое состоит из не общих элементов множеств и , т.е.

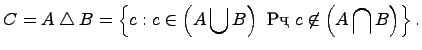
7. Дополнение множества: .

Если предположим, что множество является подмножеством некоторого универсального множества , тогда определяется операция дополнения:

   и

8. Вхождение одного множества в другое множество: .

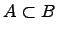Если любой элемент множества является элементом множества , то говорят, что множество есть подмножество множества (множество входит в множество ).

9. Не вхождение одного множества в другое множество: .

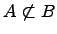Если существует элемент множества , который не является элементом множества , то говорят, что множество не подмножество множества (множество не входит в множество ).

Верхняя и нижняя грань множества

Определение 3. Элемент частично упорядоченного множества называется максимальным³⁾, если влечет за собой .

Определение 4. Элемент частично упорядоченного множества называется минимальным⁴⁾, если влечет за собой .

Если множество линейно упорядочено, то минимальный и максимальный элементы этого множества, если они существуют, определены единственным образом и называются наименьшим и наибольшим элементом множества, соответственно.

Определение 5. Пусть — подмножество частично упорядоченного множества . Говорят, что элемент — верхняя грань⁵⁾ для множества , если для всех . Минимальный элемент среди всех верхних граней для множества , если он существует, называется наименьшей верхней гранью⁶⁾ для множества .

Определение 6. Пусть — подмножество частично упорядоченного множества . Говорят, что элемент — нижняя грань⁷⁾ для множества , если для всех . Максимальный элемент среди всех нижних граней для множества , если он существует, называется наибольшей нижней гранью⁸⁾ для множества .

Теорема о точной грани :

2. Числовая посл. представляет собой нумерованные числа, задаётся формулой. Возрастающая посл.-если следующее число больше предыдущего. Бывают сходящимися или имеющие предел и расходящимися. Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами.

Бесконечно малые.

Переменная называется бесконечно малой, если для любого существует такое значение , что каждое следующие за ним значение будет по абсолютной величине меньше .

Если - бесконечно малая то говорят, что стремится к нулю, и пишут: .

Бесконечно большие.

Переменная x называется бесконечно большой, если для всякого положительного числа c существует такое значение , что каждое следующее за ним x будет по абсолютной величине больше . Пишут:

Величина, обратная к бесконечно большой, есть величина бесконечно малая, и обратно.