Вопрос 14
Метод уменьшения помехи.
Полагаем, что в обоих направлениях частота дискретизации одинаковая.
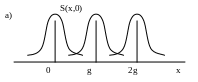
Поскольку спектр реальных изображений не ограничен по пространственным частотам, то наложения избежать невозможно, но можно ограничить путем увеличения частот пространственной дискретизации.
На рисунке (а) частота дискретизации выше, на рисунке (б) ниже.
1. Сначала при оцифровке изображения
выполняется первичная дискретизация
с круговой частотой
,
которая в n раз превышает
основную частоту пространственной
дискретизации. Достигается это за счет
того, что интервал дискретизации на I
этапе берется в n раз
меньше, чем тот, с которым в дальнейшем
изображение (б) записано в память.
Благодаря такому выбору частоты основной
и побочный спектр изображения оказывается
сильно разнесены друг относительно
друга на рисунке (б).
2. На втором этапе предварительно
дискретизированное изображение
подвергается пространственной фильтрации
путем его свертки с импульсной функцией
типа
. благодаря чему останутся только те
компоненты пространственного спектра,
которые должно удовлетворять условию:
- целые числа
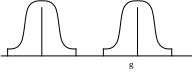
3. 3. Третий этап – передискретизация
отфильтрованного изображения, в
результате которой частота дискретизации
становится равна
.
Достигается это путем прореживания
отсчетов N раз. В результате
этой операции количество отсчетов на
изображении уменьшается до величины,
обеспечивающей выполнение теоремы
отсчетов, а спектральная интенсивность
будет выглядеть:
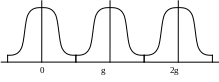
На практике достаточно повысить предварительно частоту дискретизации в 2-3 раза по отношению к основной.
Этот метод может быть применен для ослабления помехи временной дискретизации движущегося изображения.
Вопрос 15
Виды растров, применяемых при дискретизации изображения.
В общем случае спектр изображения
ограничен прямоугольником (квадратом)
со сторонами
,
.
В этом случае при выполнении условия
теоремы отсчетов наблюдается более
плотная упаковка основного и побочного
спектров на частотной плоскости. Однако,
линии пространственной спектральной
интенсивности большинства изображений
скорее напоминают ромбы или квадраты,
повернутые относительно своего центра
на
.
Поэтому желая ограничить спектр реального
изображения пространственными частотами
с внесение минимальных искажений его
следует ограничивать по линиям, в
результате чего область, занимаемая
верхним спектром будет выглядеть
следующим образом:
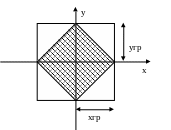
При ортогональной дискретизации чтобы
с таким спектром избежать наложения
основной и побочной компонент, необходимо
частоту дискретизации выбирать из
условия:
.
Спектр будет выглядеть следующим образом:
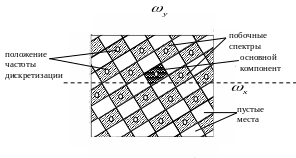
Из рисунка следует, что упаковка основного и побочного спектров на частотной плоскости не является рациональной, половина из спектров не занята.
Можно достичь более плотной упаковки
таким образом: повернем изображение на
.
Область занимаемая спектром повернутого
изображения будет иметь форму квадрата
со стороной
,
при этом ортогональная структура
расположения отсчетов с интервалом
,
где
обеспечит
наиболее плотную упаковку спектра на
частотной плоскости.
Интервал пространственной дискретизации
увеличивается в
раз, что обусловлено тем, что ширина и
высота области, занимаемой спектром
уменьшается в
благодаря повороту.
Такая структура расположения отсчетов называется шахматной. Применение этой структуры при пространственной дискретизации позволяет в 2 раза уменьшить число отсчетов на изображениях с рассматриваемым спектром, а значит и длину файлов без заметного снижения качества.
Структура расположения отсчетов на дискретизированном изображении, при котором достигается наиболее плотная упаковка основного и побочного спектров, а следовательно минимальный размер файлов, в которые она записывается, полностью определяется видом его пространственного спектра. Отсчетное изображение будет располагаться следующим образом:
Максимальная структура расположения отсчетов на изображения.
Помимо ортогональной и шахматной используют треугольную и диагональную структуры.