Вопрос 25

Статистические методы классификации.

Для этих методов необходимо, чтобы заранее было известно количество признаков и количество классов. Считается, что признаки распределены по нормальному закону, характеризуются математическом ожиданием и СКО. Если признаки являются зависимыми, то они характеризуются взаимной корреляцией.

Считается, что каждый раз предъявляется объект каждого класса и вероятность появления объектов всех классов равна сумме вероятностей появления объектов каждого класса.

Считается, что вероятность появления объекта каждого класса известна заранее.

- априорная вероятность появления объекта i-го класса.

Каждый признак объекта описывается плотностью распределения. Эта плотность выбирается условной, т.е. это плотность вероятности того, что этот признак относится к классу i.

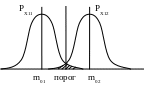
- математическое ожидание

Если предъявляемый признак меньше порога, то объект относится к первому классу, если больше, то ко второму.

Если СКВО разные, то порог смещается в сторону математического ожидания признака, имеющего меньшее СКВО.

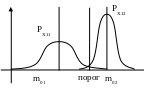
В случае одинакового СКВО сечение б. п.с.

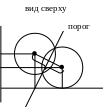
Теорема Байеса.

Эта теорема связывает априорные вероятности появления объектов классов с плотностями распределения признаков и априорная вероятность отнесения определяемого объекта к одному из классов.

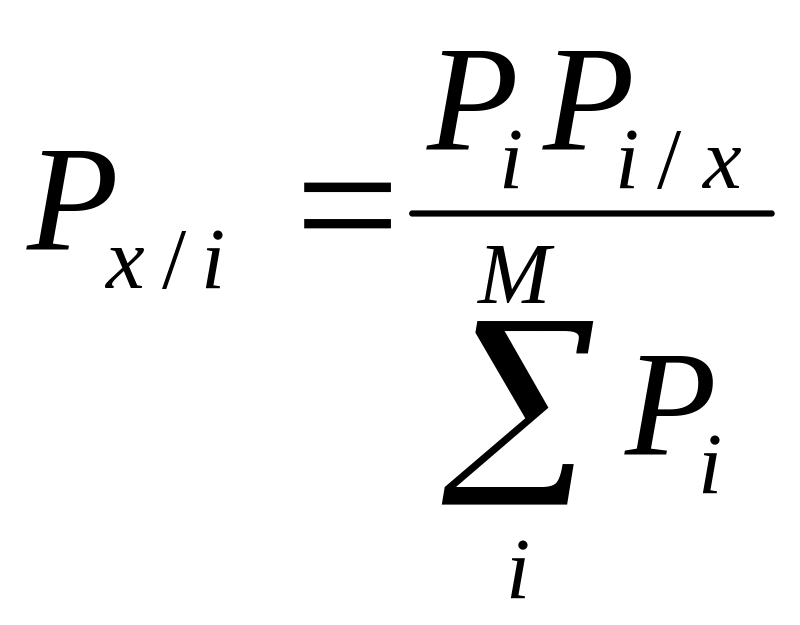
- условное распределение x класса i.

- априорная вероятность для i-го класса

- плотность распределения признака

В большинстве случаев считается, что априорная вероятность появления объектов каждого класса представляет собой единицу деленную на количество классов.

В этой теореме вводят понятие риска принятия решения, т.е. при принятии каждого решения распознающая система несет потери. Это потери при принятии решения при отнесении объекта i-го класса к j классу .

Функция потери является … и равна 0 при правильном решении и равна 1 при неправильном решении.

Вопрос 26

Вероятность ошибок при классификации.

Вероятность неправильного решения – это вероятность отнесения объекта не к тому классу: вероятность отнесения первого класса ко второму и наоборот.

(вероятность второго к первому)

(вероятность первого ко второму)

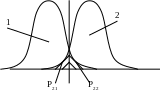
- потери

- функция потерь

- предъявлен объект первого класса и принято решение об отнесении его к первому классу

- предъявлен объект первого класса и принято решение об отнесении его к второму классу

- предъявлен объект второго класса и принято решение об отнесении его к второму классу

- предъявлен объект второго класса и принято решение об отнесении его к первому классу

Потери при неправильных решениях всегда больше чем при потерях правильных решений.

Условный риск.

Условный риск принятия решения об отнесении объекта к первому классу:

- признак

Вычисляется априорная вероятность при отнесении одного объекта к первому классу.

Для второго класса:

Отношение правдоподобия:

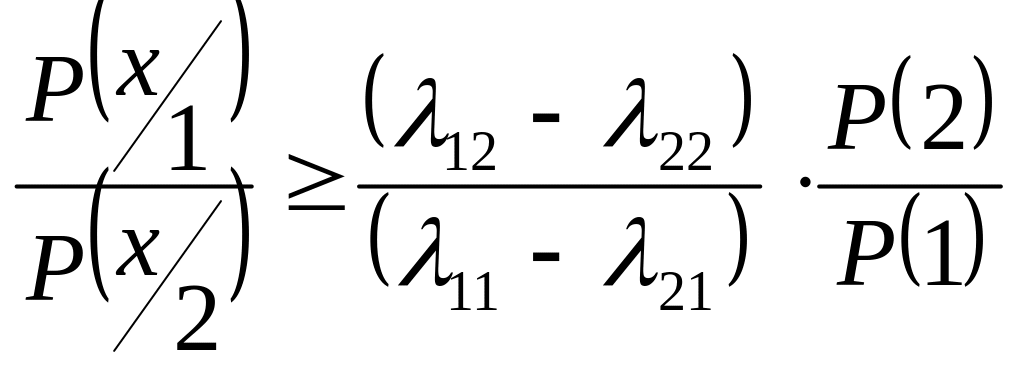
Это порог по которому принимается решение. Объект относится к первому классу, если отношение правдоподобия больше порога.

При классификации объектов больше чем двух классов вычисляется риск при принятии решения для объекта каждого класса, т.е. вычисляют всевозможные риски и принимается то решение, для которого риск минимален.

---------------------------------------------------------------------------------------------------------------

Каноническая форма классификатора.

Предполагается, что объект каждого класса характеризуется вектором признаков, которые есть у каждого класса.

Форма классификатора по двум классам:

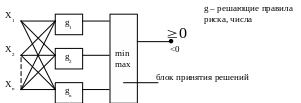
В качестве решающей функции может быть использована апостериорная вероятность.

Пример:

Для признаков распределенных по нормальному закону.

Классификация по двум классам6

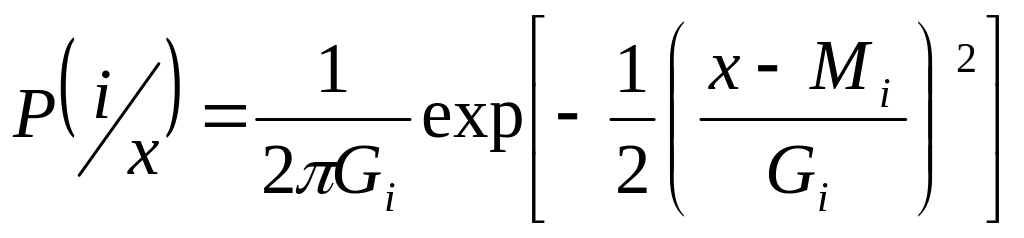
- СКО

- математическое ожидание

Сформируем отношение правдоподобия учитывая, что потери одинаковые. При принятии правильного решения:

При неправильном решении:

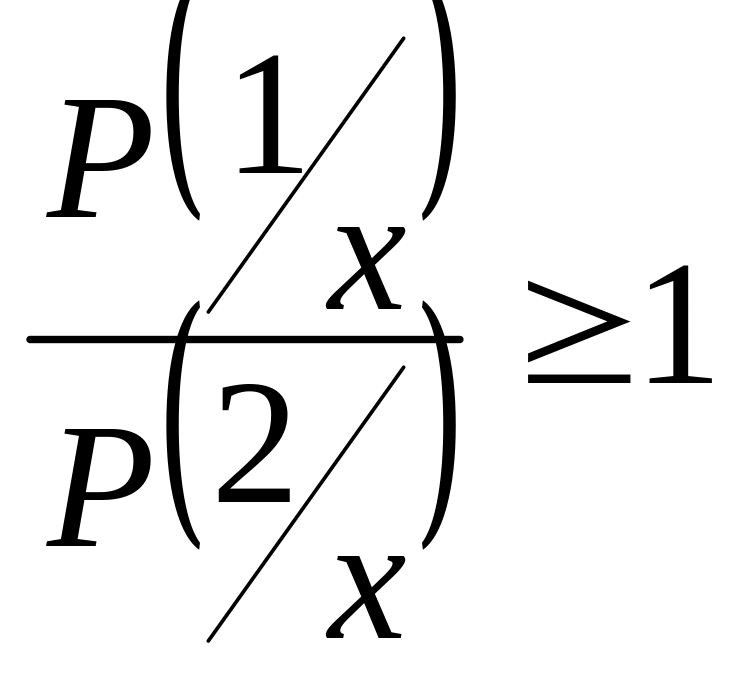
Часто в качестве отношения правдоподобия используется функция .

правило отнесения к первому классу

Для получения порога это выражение приравнивают к нулю (при одинаковых вероятностях).

Если СКО не равны, то порог будет смещаться.

Вероятность правильного решения:

Вероятность ошибки:

Некоторые особенности классификации при многомерном нормальном распределении узлов.

В этом случае каждый признак характеризуется вектором математических ожиданий с ковариационной матрицей.

Ковариационная матрица – это связь между двумя признаками.

Если , то признаки считаются независимыми.

Если , то пространственная классификация будет.

В случае, если , то:

В каком случае искажение признаком можно считать нормальным:

1. Когда все искажения признаком связаны с аддитивными шумами.

2. Когда ошибки в измерениях связаны со случайным возмещением объекта на рабочем столе.

Когда в изображении присутствуют мультипликативное изображение, нельзя принимать гипотезу о .

Все эти методы применяются только к выпуклым пространственным признакам.

Распознавание и классификация с учителем.

Ранее рассматривались методы, при которых считалось, что все признаки определены заранее и в процессе классификации в распознающей системе ничего не меняется.

Обучение с учителем – это метод адаптивной классификации, при котором на этапе обучения распознающая система определяет порог классификации, при этом в процессе обучения в системе определяется объект с указанием к какому именно классу он принадлежит.. если система имела правильное решение, то она «поощряется». Если система имела неправильное решение, то она «наказывается». Этот процесс продолжается до тех пор, пока все предъявляемые эталонные объекты не будут классифицированы правильно. На этом процесс обучения заканчивается. Система начинает функционировать в рабочем режиме.

Вектор признаков некоторого объекта i-го класса:

Определяется решающая функция – это сумма весовых коэффициентов умноженная на некоторую функцию от признака:

Задача распознающей системы на этапе обучения – подобрать такой набор весовых коэффициентов, обеспечивающих минимальные для данного класса значения решающей функции.

В большинстве случаев в ситуациях обучения с учителем используется линейная решающая функция.

- порог

Кроме этого вводят понятие обобщенной решающей функции.

В случае двух классов адаптация идет по следующему правилу:

II класс

I класс

Алгоритм подбора коэффициентов для случая двух классов:

объект		решение	Коррекция
		правильное
		правильное
		неправильное
		неправильное

Корректируемая величина должна быть положительной.

Каноническая форма классификатора с учителем:

Метод перцептрона

Вектор признаков дополняется единицами, причем в отличии от классической системы единица становится в последнем элементе вектора. Такая перестановка приводит к тому, что величина S при неправильном решении при отнесении объекта ко второму классу становится меньше нуля.

Основное условие для выбора величины S это обеспечение сходимости алгоритма подбора весов, т.е. число шагов адаптации должно быть конечным. Для перцептронного критерия сходимость обеспечивается всегда, если величина S=1.

Метод потенциальных функций.

Потенциал наводимый элементарным зарядом в некоторой точке поля обратно пропорционален расстоянию от этой точки до точки расположения зарядов.

- величина i-го заряда.

При методе потенциальных функций в системе распознавания предполагается, что каждый объект в пространстве признаков расположен на вершине некоторого плато и вершины этих плато разделены между собой соответствующими линиями равного потенциала.

Существует два вида потенциальных функций:

1.

2.

- место расположения неизвестного объекта

- место расположения вектора признака эталонного класса i

- потенциал точки с неизвестным объектом

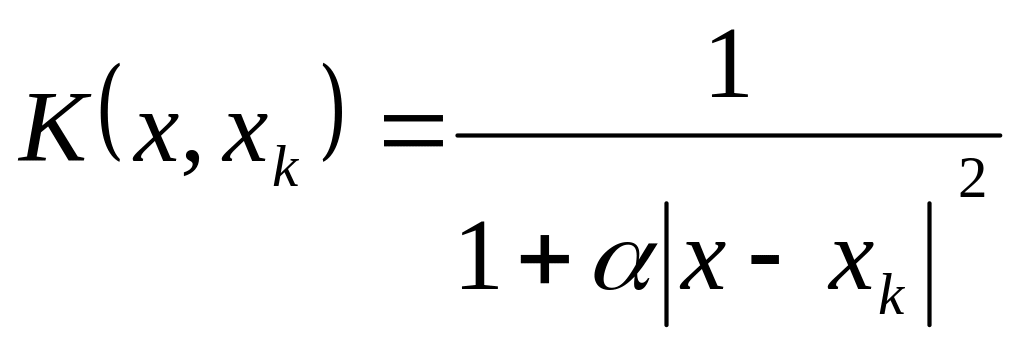функцию относят ко второму классу

Все три функции – потенциальные функции второго рода.

- потенциальная функция второго рода

- вектора признаков объекта первого или второго класса предъявляемых на К-ом шаге операции.

Это решающая функция в методе потенциальных функций.

- номер шага

Коэффициент при правильном решении на шаге будет -1, если объект принадлежит к первому классу, но отнесен ко второму. И , если наоборот (принадлежит ко второму, а отнесен к первому).

В большинстве случаев используется коммуникативный потенциал.

1 шаг