Вопрос 23

Определение центра тяжести и центра формы объекта.

- координаты центра формы

Формулы справедливы для прямоугольников, квадратов, треугольников и кругов.

Формулы используются для бинарных изображений.

- общее число точек принадлежащих объекту

- количество точек по вертикали

- количество точек по горизонтали

- номер точки по горизонтали и по вертикали

- значение яркости в конкретной точке

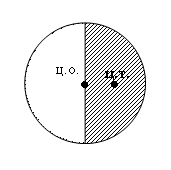
При определении центра тяжести объекта координаты суммируются с весами что эквивалентно яркости этой точки. Центр тяжести объекта может не совпадать с центром формы, он смещается в сторону более яркого объекта.

Применяются для двутоновых изображений.

Задача: определить центр тяжести объекта.

Определим момент инерции по осям и главный момент инерции.

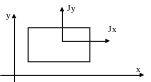
Смешанный момент инерции:

Главный момент инерции:

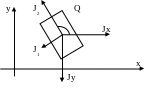
- угол ориентации объекта в пространстве

,

Вопрос 24

Классификация объектов.

На этапе классификации необходимо определить к какому из заранее заданных классов объектов относится определяемый объект. Для этого необходимо описать объект на языке признаков. При этом количество признаков для объектов разных классов должно быть одинаковое. Обычно говорят о пространстве признаков. В случае классификации по единственному признаку пространство признаков однородное и все объекты классифицируются по значению этого признака.

Методы классификации.

1. По методу описания признаков:

1) Детерминированные признаки – характеристики объектов точно известны.

2) Вероятностные, когда признаки объектов описываются статистически, т.е. известны только законы распределения значений признаков.

3) Синтаксические.

2. По методу работы.

1) Методы с обучением

2) Методы без обучения

При классификации без обучения алгоритм работы системы (принятия решения) задается до начала её работы на этапе проектирования.

В системах с обучением параметры классификатора неизвестны. Система определяет их сама в процессе обучения. После обучения система приступает к работе, а параметры признаков сохраняются.

Системы с обучением бывают: с учителем и без учителя (системы искусственного интеллекта).

Метод сравнения с эталоном.

Имеется m классов объектов и n классов признаков. В этом случае каждый объект описывается n признаков.

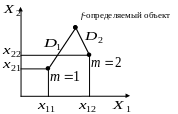
Имеется два класса, у каждого класса есть эталон. Когда появляется неизвестный объект , то определяется расстояние от него эталонов и . Объект относится к тому классу, расстояние до которого меньше.

В качестве расстояния используется либо стандартная метрическая мера, либо взвешенная дисперсия (используется в большинстве случаев).

Метрическая мера должна удовлетворять нескольким условиям:

1.

2.

Эта мера работает, когда порядки пространственных признаков у классифицируемых объектов одинаковые. В других случаях вводятся специальные нормировки. В качестве такой нормировки используется взвешенная дисперсия. Например, предъявляется значений признаков. По нему определяется математическое ожидание и дисперсия.

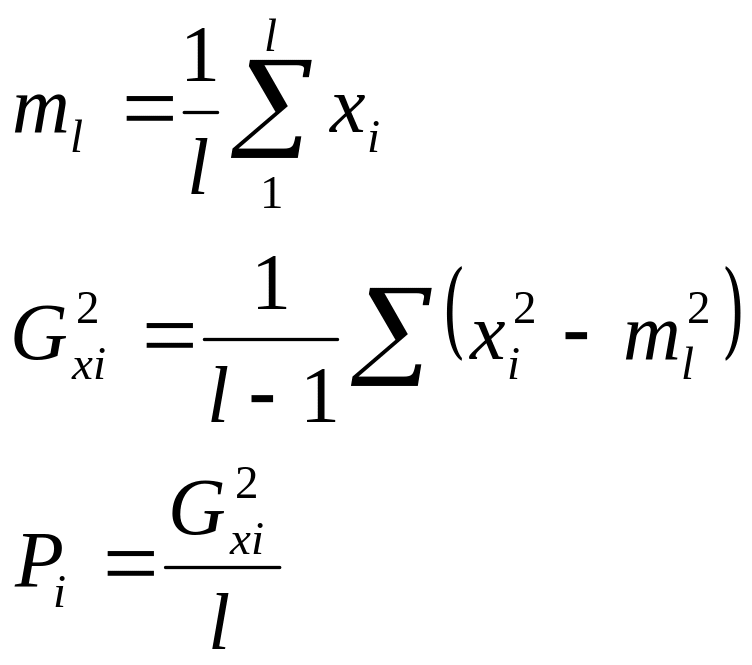
- взвешенная дисперсия для каждого i-го признака

Есть ситуация, когда признаки не имеют числового значения ( есть признак, нет признака).

	гайка	винт	шайба
резьба	1	1	0
отверстие	1	0	1
грани	1	0	0

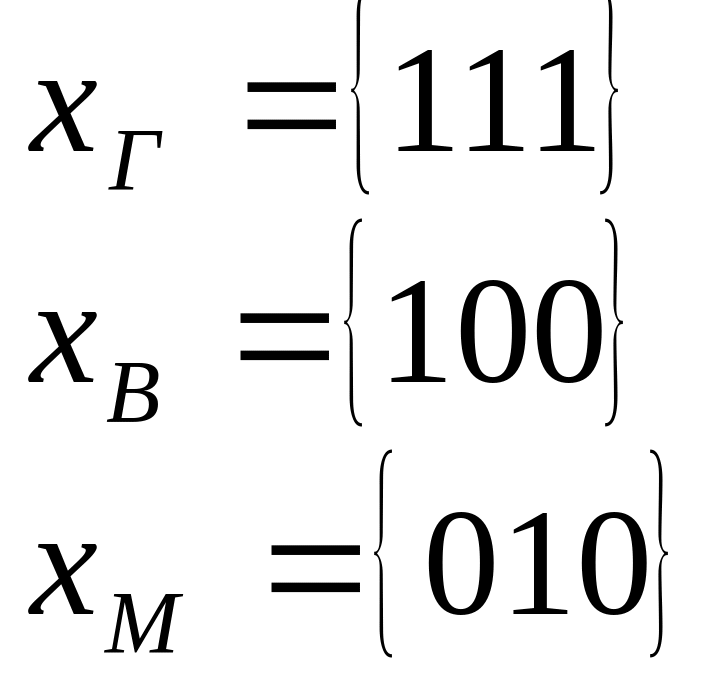
Делается пара предъявлений: один объект, который необходимо классифицировать, второй – один из эталонов.

	Xm
Xe	a	h
	g	b

- количество совпадений признака и эталона

- количество несовпадений

- количество ситуаций, кода признаки первого объекта находятся у эталона

- отсутствуют признаки

Для принятия решений используются следующие правила:

1. , где - количество признаков

Общее решение , по которому принимается решение по принадлежности класса к какому-либо эталону.

2.

3.

4.

Скелетизация объектов.

Скелет – геометрическое место точек, в которое превращается фигура при стягивании всех точек контура с одинаковой скоростью к центру формы фигуры, такое, что всегда найдется точка скелета, для которой расстояние до двух точек контура одинаковое.

Скелетизация широко используется в методах распознавания символов.