1.Диаграмма рассеяния.

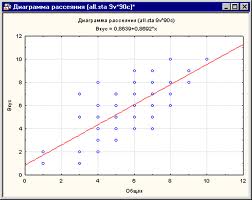
Диаграмма рассеяния (рассеивания) -- диаграмма, составленная из точек на координатной плоскости. Диаграммы рассеяния применяют для изучения связей между двумя различными характеристиками, например, ростом и весом животного и т.д. При этом абсцисса и ордината каждой точки на диаграмме -- значения этих характеристик.

Если на плоскости мы видим "облако" точек, вытянутое от левого нижнего угла к правому верхнему, то можно говорить о наличии положительной связи между признаками, т.е. с ростом одного признака другой в среднем растет. Если же это "облако" точек вытянуто от левого верхнего угла к правому нижнему, то характер связи отрицательный, т.е. с ростом одного признака другой признак в среднем убывает. Если "облако" точек вытянуто по горизонтали, по вертикали или же точки более-менее равномерно заполняют круг, то связь между признаками, скорее всего, отсутствует.

На практике применяют также трехмерные диаграммы рассеяния, которые в школьном курсе не изучаются. Их используют для сравнения между собой трёх характеристик. В этом случае точки изображаются в координатном пространстве. Абсцисса, ордината и аппликата каждой точки -- значения этих характеристик.

2.Линейная модель парной регрессии

Построение модели парной регрессии заключается в нахождении уравнения связи двух показателей у и х, т.е. определяется как повлияет изменение одного показателя на другой. Основной задачей является нахождение параметров модели и оценке их качества. Уравнение модели парной регрессии можно записать в общем виде:

где у - зависимый показатель (результативный признак);

х - независимый, объясняющий фактор.

Уравнение парной линейной регрессии:

у = а + bx

3. Линейная модель множественной регрессии

Множественная регрессия – уравнение связи с несколькими независимыми переменными:

где y - зависимая переменная (результативный признак);

- независимые переменные (факторы).

Недостаток множ. регр.: она является линейной, определяющие факторы не зависят друг от друга и существует «проклятие размерности». Но существует метод снижения размерности: проверяют не связаны ли какие-то переменные с помощью к-та корреляции, если они св-ны, то уменьшают размерность.

6. МНК

Метод наименьших квадратов (МНК) - метод оценки параметров модели на основании экспериментальных данных, содержащих случайные ошибки. В основе метода лежат следующие рассуждения: при замене точного (неизвестного) параметра модели приблизительным значением необходимо минимизировать разницу между экспериментальными данными и теоретическими (вычисленными при помощи предложенной модели). Это позволяет рассчитать параметры модели с помощью МНК с минимальной погрешностью.

Мерой разницы в методе наименьших квадратов служит сумма квадратов отклонений действительных (экспериментальных) значений от теоретических. Выбираются такие значения параметров модели, при которых сумма квадратов разностей будет наименьшей – отсюда название метода:

= min

где Y – теоретическое значение измеряемой величины, y – экспериментальное.

При этом полученные с помощью МНК параметры модели являются наиболее вероятными.

Метод наименьших квадратов, а также его различные модификации (нелинейный МНК, взвешенный МНК и т.д.) широко используется в аналитической химии, в частности, при построении градуировочной модели. Как правило, предполагается линейная зависимость (параметры которой требуется установить) между аналитическим сигналом и содержанием определяемого вещества. В этом случае метод наименьших квадратов позволяет оптимизировать параметры градуировки (и получить наименьшую погрешность анализа), а сумма квадратов разностей теоретического и экспериментального значения аналитического сигнала является мерой погрешности градуировки и линейно связана с так называемой остаточной дисперсией (дисперсией адекватности модели)