
- •Источники эдс и тока и их взаимное преобразование.
- •2.Электрическая цепь, основные величины и понятия. Мгновенная мощность и энергия.
- •3.Законы Кирхгофа. Расчет эц по закона Кирхгофа.
- •5. Перенос источников эдс в схеме из ветви в другие ветви
- •6.Объединение нескольких параллельных ветвей в одну экви-ю.
- •7. Метод контурных токов.
- •8. Метод узловых потенциалов. Пример расчета электрических цепей на основе муп.
- •9.Теорема наложения и метод расчета эл.Цепей.
- •10. Теорема компенсации
- •13.Потенциальная или топографическая диаграмма(д)
- •14.Энергетический баланс в эл.Цепях.
- •16. Синусоидальный ток в последовательной r, l, c – цепи
- •18.Мощность в цепи синусоидального тока. Активная, реактивная и полная мощности.
10. Теорема компенсации
Ток в любой ветви схемы не изменится, если сопротивление этой ветви заменить ист.ЭДС, направление которого противоположно падению напряжения на этом сопротивлении, а величина равна падению напряжения.
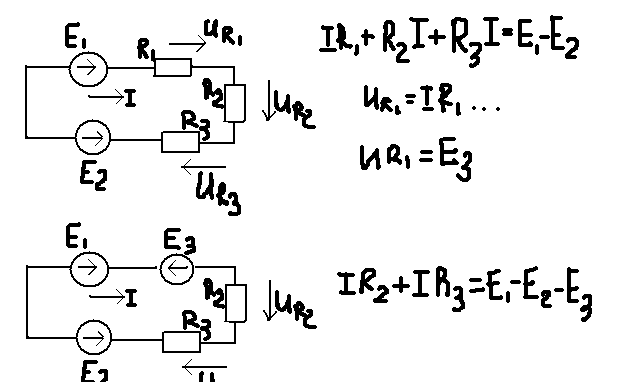
11.Ток в любой ветви разветвленной схемы не изменится, если эту схему заменить источником ЭДС(тока), величина которого равна напряжению холостого хода на зажимах данной ветви(току короткого замыкания), а внутр.сопротивление этой ЭДС равно входному сопротивлению данной цепи по отношению к зажимам разомкнутой цепи. Разбиваем на 2 схемы по методу наложения
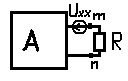
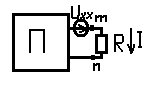
В первой схеме (там где А) ток будет равен 0, во втрой схеме ток будет равен
I=Umnxx/(Rг+R); (*)
По формуле (*) определяется ток
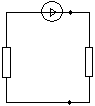
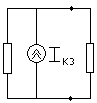
Метод эквивалентного генератора тока. Алгоритм решения задач на основе настоящего метода. Теорема Нортона : ток в любой ветви mn линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником тока алгоритм решения:
Uхх m
![]()
m I
Rг R Rг R
n
n

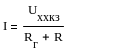
Находим Rг. Находим Iкзmn, для чего исследуемую ветвь заменяем перемычкой (короткое замыкание).Окончательно получим:
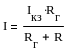
13.Потенциальная или топографическая диаграмма(д)
Потенциальная диаграмма – это графическое оборажение второго закона Кирхгофа (Сумма падений напряжений по замкнутому контуру равна 0).
1)выберем контур, по кот.будем строить.
2)выберем точку начала 3) выберем обход контура 4)оценим масштаб.суммируем все R/
14.Энергетический баланс в эл.Цепях.
Все, Что отдается в схему, Потребляется приемником.
Ист.энергии: ист.ЭДС, ист.Тока
Приемники энергии: сопротивления , ист.ЭДС, ист.тока
С точки зрения баланса энергия, потребляемая пассивными элементами, положительна. А энергия, кот. Отдается ист.энергии, всегда отрицательна.
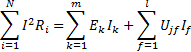
k-текущий индекс ист.ЭДС в схеме;m-общее кол-во
f- текущий индекс ист.тока в схеме;l-кол-во ист.тока
15.Синусоидальный ток а активном сопротивлении, индуктивности, емкости.
Активн. Сопротивление-идеализиров.сопротивление, приблииженное по своим свойствам к резистору, в кот. Происходит процесс превращения энергии в тепло.
![]()
![]() ;
Im=
;
Im=![]() ;
;
![]()
P=U*I=![]()
Отсюда следует, что в активном сопротивлении мощность расходится:
1)больше 0
2)Колеблется с удвоенной частотой по отношению к частоте напряжения тока I
Синусоидальный ток индуктивности
Индуктивность
– идеализированный элемент цепи,
приближенный к катушке индуктивности,
в кот. Происходит накопление магнитной
энергии, численно равной потоку сцепления
i.![]()
На
зажимах индуктивности возникают по
з-ну Максвелла-Фарадея ЭДС самоиндукции,
по з-ну Ленца это ЭДС направлено навстречу
току
![]()
![]()
![]() (Ом)
(Ом) ![]() (Cм)
(Cм)
Напряжение
опережает ток на 90о
.Мощность: ![]() Мощность с удвоенной частотой будет
колебаться относительно О. В индукт.
Мощность не потребляется, а запасается
в «+», а в «-» (отрицательный полупериод)
отдается обратно в схему
Мощность с удвоенной частотой будет
колебаться относительно О. В индукт.
Мощность не потребляется, а запасается
в «+», а в «-» (отрицательный полупериод)
отдается обратно в схему
Синусоидальный ток емкости
Емкость
–элемент цепи, приближенный по свойствам
к конденсатору, в кот.накапливается
энергия в виде эл.поля. На обкладках
конденсатора накапливается заряд q=CU,
изменяясь во времени возникает ток. ![]()
![]()
![]()
![]() )
)
![]() Мощность в конденсаторах не расходуется,
а запасается в полож.полупериоды и
отдается в отрицательные.
Мощность в конденсаторах не расходуется,
а запасается в полож.полупериоды и
отдается в отрицательные.
