
- •1.Совершенные нормальные формы.Правила приведения к сднф и скнф. Минимизация логических функций.
- •§8. Нормальные формы функций.
- •8.2 Нормальные формы.
- •8.3 Совершенные нормальные формы.
- •8.4 Правила приведения произвольной формулы алгебры логики к совершенной нормальной форме.
- •8.6 Способ составления снф для произвольной формулы алгебры логики по таблице истинности.
- •§ 1. Понятие формулы исчисления высказываний.
- •§ 2. Определение доказуемой (выводимой) формулы.
- •Правила вывода.
- •Определение выводимой (доказуемой ) формулы.
- •Правило сложной (одновременной) подстановки (спп).
- •Правило сложного заключения.
- •Правило силлогизма.
- •Правило контр позиции.
- •Правило снятия двойного отрицания.
- •§4.Понятие выводимости формул из совокупности формул.
- •§5. Понятие вывода.
- •§6. Правила выводимости.
- •H,w├a из совокупности формул : “Если а выводима из н, то она вы- водима из ”.
- •5. Теорема дедукции: h, c├ a .
- •§9.Проблемы аксиоматического исчисления высказываний.
- •2. Проблема непротиворечивости исчисления высказываний.
- •3.Проблема полноты исчисление высказываний.
- •4.Проблема независимости аксиом исчисления высказываний.
- •§1. Недостаточность логики высказываний. Понятие предиката.
- •§2. Логические операции над предикатами.
- •§3. Кванторные операции.
- •Квантор всеобщности.
- •Квантор существования.
- •Отрицание предложений с кванторами.
- •§4.Понятие формулы логики предикатов.
- •§5. Значение формулы логики предикатов.
- •§6. Равносильные формулы логики предикатов.
- •§7. Нормальные формы формул логики предикатов.
- •§8. Общезначимость и выполнимость формул. Проблема разрешимости.
- •§9. Применение языка логики предикатов для записи математических предложений, определений, построения отрицания предложений.
- •9.1 Запись математических предложений и определений в виде формул логики предикатов.
- •9.2. Построение противоположный утверждений.
- •9.3 Прямая, обратная и противоположная теоремы.
- •9.4 Необходимые и достаточные условия.
- •9.5. Доказательство теорем методом от противного.
- •Утверждения о свойствах объектов и отношениях между ними
- •Язык логики предикатов
- •Синтаксис: формулы логики предикатов
- •Семантика: системы и значения формул на их состояниях
- •Реляционные базы данных
- •Реляционная алгебра
- •Теоретико-множественные операции
- •Специальные реляционные операторы
- •Запросы
- •Ограничения целостности
- •Основные определения
- •Тьюрингово программирование
- •Стандартная заключительная конфигурация
- •Односторонние машины Тьюринга
- •Последовательная и параллельная композиции машин Тьюринга
- •Ветвление (условный оператор)
- •Повторение (цикл)
Правила вывода.
1 Правило подстановки(ПП).
Если формула А выводима (доказуема) в исчислении высказываний, х- переменная, В- произвольная формула исчисления высказываний, то формула , полученная в результате замены в формуле А переменной х всюду , где она входит, формулой В, является также выводимой(доказуемой) формулой (ситуация та же, что имела место в алгебре логики, которая является интерпретацией исчисления высказываний).
Операция замены в формуле А переменной х формулой В, носит название подстановки и символически записывается так:
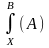 или
или
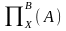 .
.
Уточним сформулированное правило:
а) если формула А есть собственно переменная х , то подстановка дает , очевидно, В;
б) если формула А есть переменная y , отличная от х ,то подстановка дает А;
в)подстановка
формулы В вместо х в отрицание формулы
А есть отрицание подстановки , т. е.
подстановка
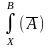 дает
дает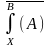 ;
;
г) если А1 и
А2- некоторые формулы, то подстановка
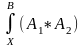 дает
дает
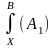 *
*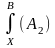 ,
где через символ * обозначен любой из
символов операций конъюнкция, дизъюнкция
или отрицание
,
где через символ * обозначен любой из
символов операций конъюнкция, дизъюнкция
или отрицание
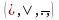
Если А- выводимая (доказуемая ) формула, то будем писать, как и ранее, ├А. Тогда ПП можно записать схематически следующим образом:
├А____ .
├
И читается эта запись так: “Если формула А выводима (доказуема), то выводима (доказуема) и формула .
2 Правило заключения (ПЗ).
Если формулы А и А→В выводимы (доказуемы) в исчислении высказываний, то формула В также выводима (доказуема). Схематическая запись этого правила имеет вид:
├А;├А→В (Modus ponens)
├В
Правомерность этого правила очевидна: если импликация и посылка истинны, то заключение в импликации может быть только истинным(см. таблицу истинности операции “импликация”).
Определение выводимой (доказуемой ) формулы.
а) Всякая аксиома является доказуемой формулой.
б)Формула, полученная из доказуемой формулы путем применения подстановки вместо переменной х произвольной формулы В, есть доказуемая формула.
в) Формула В,
полученная из доказуемых формул А и
 путем применения ПЗ, есть доказуемая
формула.
путем применения ПЗ, есть доказуемая
формула.
г) Никакая другая формула исчисления высказываний не считается доказуемой .
Процесс получения доказуемых формул будем называть доказательством (выводом) формул. Это процесс последовательного перехода от одной доказуемой формулы к другой с помощью аксиом, правила подстановки и правила заключения на каждом шаге (в определенном смысле это аналог равносильным преобразованиям в алгебре логики), так что вывод даже простой формулы может оказаться, в силу его многошаговости, достаточно громоздким.
3. §3. Производные правила вывода.
Производные правила вывода, как и рассмотренные правила подстановки и заключения, позволяют получать новые доказуемые формулы. Они получаются с помощью правил подстановки и заключения, а поэтому являются производными от них.
Правило сложной (одновременной) подстановки (спп).
Пусть А – доказуемая
формула;
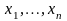 -
переменные, а
-
переменные, а
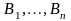 -
любые формулы ИВ. Тогда результат
одновременной подстановки в формулу А
вместо
соответственно формул
является доказуемой формулой.
-
любые формулы ИВ. Тогда результат
одновременной подстановки в формулу А
вместо
соответственно формул
является доказуемой формулой.
Схематично операция СПП записывается так:
├А______
├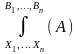
Так, в рассмотренном выше примере вместо шагов 4-5-6 и 9-10-11 можно было сразу применить СПП и тогда вместо 12 получим желаемый результат за 8 ходов:
1) . . . .( ) (1)
2)
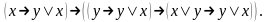 . . .
. . .
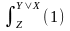 (2)
(2)
3)
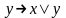 . . .(
)
(3)
. . .(
)
(3)
4)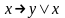 . . .
. . .
 (4)
(4)
5)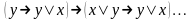 (2),(4), ПЗ . (5)
(2),(4), ПЗ . (5)
6)
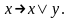 . . . (
)
(6)
. . . (
)
(6)
7)
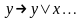
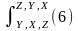 (7)
(7)
8)
 . . . (5), (7), ПЗ (8)
. . . (5), (7), ПЗ (8)
