
- •1.Совершенные нормальные формы.Правила приведения к сднф и скнф. Минимизация логических функций.
- •§8. Нормальные формы функций.
- •8.2 Нормальные формы.
- •8.3 Совершенные нормальные формы.
- •8.4 Правила приведения произвольной формулы алгебры логики к совершенной нормальной форме.
- •8.6 Способ составления снф для произвольной формулы алгебры логики по таблице истинности.
- •§ 1. Понятие формулы исчисления высказываний.
- •§ 2. Определение доказуемой (выводимой) формулы.
- •Правила вывода.
- •Определение выводимой (доказуемой ) формулы.
- •Правило сложной (одновременной) подстановки (спп).
- •Правило сложного заключения.
- •Правило силлогизма.
- •Правило контр позиции.
- •Правило снятия двойного отрицания.
- •§4.Понятие выводимости формул из совокупности формул.
- •§5. Понятие вывода.
- •§6. Правила выводимости.
- •H,w├a из совокупности формул : “Если а выводима из н, то она вы- водима из ”.
- •5. Теорема дедукции: h, c├ a .
- •§9.Проблемы аксиоматического исчисления высказываний.
- •2. Проблема непротиворечивости исчисления высказываний.
- •3.Проблема полноты исчисление высказываний.
- •4.Проблема независимости аксиом исчисления высказываний.
- •§1. Недостаточность логики высказываний. Понятие предиката.
- •§2. Логические операции над предикатами.
- •§3. Кванторные операции.
- •Квантор всеобщности.
- •Квантор существования.
- •Отрицание предложений с кванторами.
- •§4.Понятие формулы логики предикатов.
- •§5. Значение формулы логики предикатов.
- •§6. Равносильные формулы логики предикатов.
- •§7. Нормальные формы формул логики предикатов.
- •§8. Общезначимость и выполнимость формул. Проблема разрешимости.
- •§9. Применение языка логики предикатов для записи математических предложений, определений, построения отрицания предложений.
- •9.1 Запись математических предложений и определений в виде формул логики предикатов.
- •9.2. Построение противоположный утверждений.
- •9.3 Прямая, обратная и противоположная теоремы.
- •9.4 Необходимые и достаточные условия.
- •9.5. Доказательство теорем методом от противного.
- •Утверждения о свойствах объектов и отношениях между ними
- •Язык логики предикатов
- •Синтаксис: формулы логики предикатов
- •Семантика: системы и значения формул на их состояниях
- •Реляционные базы данных
- •Реляционная алгебра
- •Теоретико-множественные операции
- •Специальные реляционные операторы
- •Запросы
- •Ограничения целостности
- •Основные определения
- •Тьюрингово программирование
- •Стандартная заключительная конфигурация
- •Односторонние машины Тьюринга
- •Последовательная и параллельная композиции машин Тьюринга
- •Ветвление (условный оператор)
- •Повторение (цикл)
Односторонние машины Тьюринга
Машина Тьюринга называется односторонней, если в процессе вычисления ее головка никогда не сдвигается левее начальной ячейки (т.е. всегда находится в ячейках с положительными номерами).
Лемма 9.2. Для всякой м.Т. можно построить эквивалентную одностороннюю м.Т. .
Доказательство.
Пусть ![]() .
Будем считать (используя лемму 1 ),
что
завершает
работу в стандартных
конфигурациях.
Требуемая м.Т.
будет
моделировать работу
,
используя "многоэтажную" ленту. Содержимое
ячеек на 1-ом (нижнем) этаже будет на
каждом такте совпадать с содержимым
тех же ячеек
,
на 2-ом этаже будет копироваться содержимое
левой полуленты: на нем в i -ой
ячейке
будет
тот же символ, что и в -i -ой
ячейке
.
Кроме того, на 3-ем этаже в 1-ой ячейке
будет стоять отмечающий ее символ #.
Таким образом,
.
Будем считать (используя лемму 1 ),
что
завершает
работу в стандартных
конфигурациях.
Требуемая м.Т.
будет
моделировать работу
,
используя "многоэтажную" ленту. Содержимое
ячеек на 1-ом (нижнем) этаже будет на
каждом такте совпадать с содержимым
тех же ячеек
,
на 2-ом этаже будет копироваться содержимое
левой полуленты: на нем в i -ой
ячейке
будет
тот же символ, что и в -i -ой
ячейке
.
Кроме того, на 3-ем этаже в 1-ой ячейке
будет стоять отмечающий ее символ #.
Таким образом, ![]() .
Работа
будет
происходить следующим образом.
.
Работа
будет
происходить следующим образом.
1) На первом этапе отмечается 1-я ячейка и содержимое входа переписывается на 1-ый этаж трехэтажной ленты:

Затем моделирует работу , используя для работы на 2-ом этаже дубликаты состояний (со штрихами) и команды со сдвигами в обратном направлении. Для команды q ,a -> r , b ,C из P и для всех
 в P' поместим команды:
в P' поместим команды:

Кроме
того, для ![]() сохраним
и старые команды для
работы на впервые посещаемых ячейках:
сохраним
и старые команды для
работы на впервые посещаемых ячейках:
![]()
Сдвиги из 1-ой ячейки налево в -1-ю и обратно моделируются переходом с одного этажа на другой в 1-ой ячейке :

После завершения моделирования результат записан в начальных ячейках на 1-ом этаже. переводит его в первоначальный алфавит

Проверка правильности работы м.Т. предоставляется читателю (см. задачу 9.4).
Последовательная и параллельная композиции машин Тьюринга
Используя возможность моделирования произвольной м.Т. на м.Т. со стандартными заключительными конфигурациями, легко установить справедливость следующей леммы о последовательной композиции машин Тьюринга.
Лемма 9.3.( Последовательная композиция ) Пусть м.Т. вычисляет функцию f(x), а м.Т. - функцию g(x). Тогда существует м.Т. вычисляющая функцию h(x) = f(g(x)).
Доказательство Действительно,
пусть ![]() а
а ![]() .
Используя лемму 9.1, будем считать, что
у
.
Используя лемму 9.1, будем считать, что
у ![]() заключительныеконфигурации стандартны.
Тогда легко проверить, что
функция h вычисляется
следующей м.Т.
заключительныеконфигурации стандартны.
Тогда легко проверить, что
функция h вычисляется
следующей м.Т. ![]() где
где ![]() .
.
Покажем, что работу двух м.Т. можно комбинировать так, чтобы в заключительной конфигурациисодержались результаты работы каждой из них над независимыми входами.
Лемма 9.4. ( Параллельная композиция ) Пусть м.Т. вычисляет функцию f(x), а м.Т. - функцию g(x) и символ * не входит в алфавит м.Т. . Тогда существует м.Т. которая по любому входу вида x*y выдает результат f(x)*g(y), т.е. вычисляет функцию H(x*y) = f(x)*g(y).
Доказательство.
Пусть ![]() и
- м.Т.
Не ограничивая общности, будем считать,
что эти машины односторонние (по
Лемме 2). Определим теперьм.Т.
и
- м.Т.
Не ограничивая общности, будем считать,
что эти машины односторонние (по
Лемме 2). Определим теперьм.Т. ![]() ,
которая работает следующим образом.
,
которая работает следующим образом.
Начав в конфигурации (p0x*y), находит 1-ый символ y
и переходит в конфигурацию (x*q02y).
Работая как
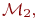 вычисляет g(y) и
переходит при этом в конфигурацию (x*qf2g(y)).
вычисляет g(y) и
переходит при этом в конфигурацию (x*qf2g(y)).Переписывает *x после g(y) и переходит в конфигурацию g(y)*q01x).
Работая как
 вычисляет f(x) и
переходит при этом в конфигурацию (g(y)*qf1f(x).
вычисляет f(x) и
переходит при этом в конфигурацию (g(y)*qf1f(x).Меняет
 и
и  местами
и останавливается.
местами
и останавливается.
Корректность
этапов 2 и 4 следует из односторонности
и ![]() а
реализация этапов 1, 3 и 5 достаточно
очевидна (см. задачу 9.6).
а
реализация этапов 1, 3 и 5 достаточно
очевидна (см. задачу 9.6).
Построенную
в этой лемме м.Т.
,
полученную в результате параллельной
композиции ![]() и
,
будем обозначать как
и
,
будем обозначать как ![]() .
Здесь индекс * указывает
символ, которым отделяются
аргументы
и
на ленте
.
Этот символ может быть любым символом,
не входящим в алфавит машины
.
Например,
.
Здесь индекс * указывает
символ, которым отделяются
аргументы
и
на ленте
.
Этот символ может быть любым символом,
не входящим в алфавит машины
.
Например, ![]() будет
обозначать параллельную
композициюмашин
и
,
в которой их аргументы отделены
символом #.
будет
обозначать параллельную
композициюмашин
и
,
в которой их аргументы отделены
символом #.
Конструкцию параллельной композиции можно обобщить на произвольное конечное число машин Тьюринга.
Следствие.
Пусть ![]() - машины
Тьюринга,
вычисляющие функции f1,
... , fm,
соответственно. Пусть символ * не
входит в алфавиты этих машин. Тогда
существует м.Т.
,
перерабатывающая любой вход вида x1*x2*
... *xm
- машины
Тьюринга,
вычисляющие функции f1,
... , fm,
соответственно. Пусть символ * не
входит в алфавиты этих машин. Тогда
существует м.Т.
,
перерабатывающая любой вход вида x1*x2*
... *xm ![]() в
выход f1(x1)*f2(x2)*
... *fm(xm).
в
выход f1(x1)*f2(x2)*
... *fm(xm).
Действительно,
в качестве
можно
взять м.Т.,
определяемую выражением ![]() .\\
Будем обозначать эту машину
Тьюринга как
.\\
Будем обозначать эту машину
Тьюринга как ![]() .
.
