Тьюрингово программирование

В этом разделе мы приведем примеры вычислений на машинах Тьюринга и рассмотрим некоторые общие приемы, позволяющие комбинировать программы различных м. Т. для получения более сложных вычислений. Будем считать, что ячейки ленты м.Т. занумерованы от   до  , причем в начальнойконфигурации головка находится в 1-ой ячейке:

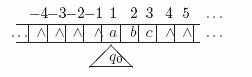
Рис. 9.2.  Нумерация ячеек ленты машины Тьюринга

Пример 9.2.Функция f(x)=x+1

• Унарное кодирование.

Пусть м.Т.  , где  .

• Ясно, что м.Т.   проходит по массиву палочек слева направо и записывает в первой пустой ячейке новую |.

• Бинарное кодирование.

Пусть м.Т.  , где  :

Нетрудно видеть, что эта машина в состоянии q₀ находит младший разряд двоичного входа, затем в состоянии q₁, идя справа налево, заменяет единицы на нули до тех пор, пока не находит 0 (или  ) и заменяет его на 1. Следовательно, м.Т.   вычисляет функцию f(x) = x+1.

Пример 9.2. Копирование.

Рассмотрим функцию копирования (дублирования) слов в алфавите   (мы предполагаем, что   ).

Для ее реализации используем один из типичных приемов Тьюрингова программирования - { it расширение алфавита}.Пусть   и  . М.Т.  , копирующая вход, работает следующим образом:

1. отмечает 1-ый символ входа, идет направо, ставит * после входа и возвращается в начало:

2. в состоянии q_a движется направо и записывает a в первую свободную ячейку:

3. возвращается в отмеченную ячейку и передвигает метку ' на одну ячейку вправо, снова переходя в состояние q₂:

4. увидев символ * в состоянии q₅, останавливается:

Из этого описания непосредственно следует, что   для любого  .

Стандартная заключительная конфигурация

Назовем заключительную конфигурацию стандартной, если в нейголовка наблюдает первый значащий символ результата, который находится в 1-ой ячейке (т.е. в той же ячейке, где начиналось входное слово).

Лемма 9.1.Для всякой м.Т.   можно построить эквивалентную м.Т.  , у которой все заключительныеконфигурации стандартны.

Доказательство. Пусть  . Определим по ней м.Т.  , которая удовлетворяет требованиям леммы. Положим  , где # - новый символ.  работает следующим образом.

1. Отмечает символ в первой ячейке штрихом и переходит в начальное состояние  .

2. Далее работает как 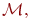  но сохраняет штрих в первой ячейке и вместо пустого символа   записывает #. Для этого для каждой команды q_ia_j -> q_k a_lC из P'

3. в P' добавляется ее дубликат q_ia_j' -> q_k a_l'C, в правых частях команд символ   всюду заменяется на # и для каждой команды вида   в P'добавляется команда q_i # -> q_k a_l C. После завершения этого этапа все посещенные в процессе работы головкой   ячейки составляет непрерывный отрезок, не содержащий пустых символов.

4. Далее   стирает ненужные символы # слева и справа от блока ячеек, содержащего первую ячейку и все ячейки с символами результата, и переходит в одну из трех следующихконфигураций:

где w - результат работы { cal M} (с заменой символов   внутри w на #) и w₁aw₂ = w.

5. Сдвигает в нужном направлении результат, совмещая его начало с ячейкой, помеченной штрихом, заменяет все # внутри w на   , снимает штрих в 1-ой ячейке и останавливается. Например, для K₁это достигается с помощью следующих команд (мы предполагаем, что ни одно из используемых ниже состояний 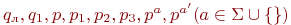  не входит в Q ):

   • поиск левого конца w: 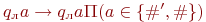  ; 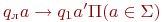  (отметили первый символ w ), 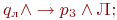  (результат пуст);

   • поиск правого конца w: 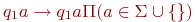 ,  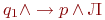 (в состоянии p наблюдает последний символ w );

   • сдвиг результата на 1 ячейку влево: 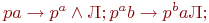  p^a b' -> p^b'aП; p^b' # -> p₁ b'П;

   • возврат к правому концу и переход к следующему сдвигу: 

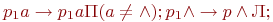
   • при сдвиге до 1-ой ячейки замена символов # на   и удаление штриха:

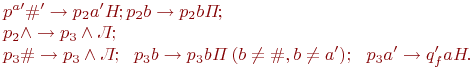
6. Из построения непосредственно следует, что м.Т.   удовлетворяет требованиям леммы.