9.4 Необходимые и достаточные условия.

Рассмотрим теорему

(1)

Как отмечалось, множество истинности предиката есть множество 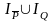. Но тогда множеством ложности этого предиката будет 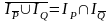. Последнее множество будет пустым лишь в случае, когда 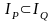(см. рисунок).

Итак, предикат является истинным для всех 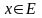том и в только в том случае, когда множество истинности предиката Р(х) содержится в множестве истинности предиката Q(x). При этом говорят, что предикат Q(x) логически следует из предиката Р(х), и предикат Q(x) называют необходимым условием для предиката Р(х), а предикат Р(х) – достаточным условием для Q(x).

Т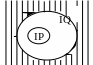 ак, в теореме “Если х – число натуральное, то оно целое ” предикат Q(x): “ х – число целое ” логически следует из предиката Р(х): “х – число натуральное” , а предикат “х- число натуральное” является достаточным условием для предиката “ х – целое число”.

Часто встречается ситуация, при которой истинны взаимно

обратные теоремы (1)

Рис. 28 .(2)

Это, очевидно, возможно при условии, что .

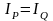В таком случае из теоремы (1)следует, что условия Р(х)являются достаточными для Q(x), а из теоремы (2) следует, что условие Р(х)является необходимым для Q(x).

Таким образом, если истинны теоремы (1) и (2), то условие Р(х) является и необходимым, и достаточным для Q(x). Аналогично в этом случае условие Q(х)является необходимым и достаточным для Р(x).

Иногда вместо логической связки “необходимо и достаточно ” употребляют логическую связку “тогда и только тогда”.

Так как здесь истинны высказывания (1) и (2), то истинно высказывание

.

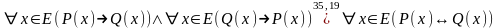9.5. Доказательство теорем методом от противного.

Доказательство теорем методом от противного обычно проводится по следующей схеме: предполагается, что теорема

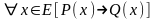(1)

не верна, т. е. , существует такой объект х, что условие Р(х) истинно, а заключение Q(x) – ложно. Если из этих предложений путем логических рассуждений приходят к противоречивому утверждению, то делают вывод о том, что исходное предположение неверно, и верна теорема (1).

Покажем, что такой подход дает доказательство истинности теоремы (1).

Действительно, предположение о том, что теорема (1) не справедлива , означает истинность ее отрицания, т. е. формулы 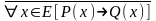. Можно показать, что противоречивое утверждение, которое получается из допущенного предположения, как мы видели из ранее рассмотренных примеров, может быть записано как конъюнкция 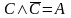, где С – некоторое высказывание.

Язык логики предикатов.

Утверждения о свойствах объектов и отношениях между ними

Утверждения, которые можно сформулировать с помощью средств логики высказываний (пропозициональной логики) всегда относятся к конкретным свойствам конкретных предметов, объектов, ситуаций. Мы уже сталкивались с примерами таких утверждений: "Сегодня идет дождь", "Вася любит Олю", "Если А - преступник, то В - не виновен", "Если цена на нефть растет и страна продает нефть, то растут и доходы ее бюджета" и т.п. Эти утверждения строятся из элементарных высказываний (пропозициональных переменных) с помощью логических связок (операций). Например, последнее из приведенных утверждений может быть формально записано как  , где X, Y иZ - это переменные, обозначющие, соответственно, высказывания " цена на нефть растет", "страна продает нефть" и "растут и доходы бюджета".

Для того, чтобы высказывать более общие точные утверждения о свойствах классов (множеств) объектов, предметов, ситуаций и т.п., нужен более богатый формальный язык. Им является язык логики предикатов (логики 1-ой ступени).

Прежде, чем переходить к формальным определениям, приведем некоторые содержательные примеры используемых понятий: объектов, свойств, отношений и операций (функций).

Объекты: люди, предприятия, числа, цвета, футбольные матчи, экзамены, дома, столы, компьютеры, фигуры, студенты, ...

Свойства: зеленый, тяжелый, голубоглазый, победный, девятиэтажный, деревянный, отличник, ...

Отношения: ... является братом ..., ... занимает должность ... с зарплатой ..., ... больше чем ..., ... находится внутри ..., ... любит ..., ... имеет цвет ..., ... случится после ..., ... владеет ..., и т.п.

Функции: отец ..., лучший_ друг ..., вдвое_больший_ чем ..., сумма ... и ..., группа_студента ..., самый_любимый_кинофильм ..., ...

В примерах отношений и функций многоточиями отмечены места, где должны стоять объекты, к которым они относятся.

Даже этих небольших перечислений достаточно, чтобы понять, что язык логики предикатов позволяет описать почти любой факт и сформулировать нужное утверждение о той или иной рассматриваемой предметной области. Вот несколько простых примеров:

" Два умножить на три равно шесть"

Здесь объекты: два, три и шесть; функция: умножить, отношение: равно.

"Все бармаглоты живут в зеленых домах"

Объекты: бармаглоты, дома; свойство: зеленый; отношение: жить_в.

"Некоторые предприятия в Твери являются банкротами"

Объекты: Тверь, предприятия; свойство: банкрот; отношение: "быть" ("являться").

С формализацией этих понятий мы уже знакомы: объекты - это множества; свойства - подмножества; а отношения и функции имеют обычный математический смысл.

Напомним некоторые определения из лекции 1. Декартовым (прямым) произведением множеств A₁, ... , A_n называется множество последовательностей длины n ( n -ок)

Если A₁= ... =A_n=A, то A₁ \times ... A_n называется декартовой (прямой) степенью множества A и обозначается через Aⁿ. Пусть A⁰ - это множество, состоящее из одной пустой последовательности  длины 0.

n -местным (или n -арным) отношением на множествах A₁,... , A_n называется любое подмножество  . Поэтому понятие свойства (подмножества) совпадает с понятием одноместного отношения. Отношение   называется n -местной (или n -арной) функцией изA₁ x ... x A_n в B, если оно для каждого набора аргументов  , содержит не более одного набора вида <a₁,..., a_n, b>. В этом случае пишем f(a₁, ..., a_n) =b.

С каждым отношением   можно связать его характеристическую функцию, которую мы будем обозначать той же буквой,

Как обычно, будем ассоциировать 1 с логическим значением "истина", а 0 - со значением "ложь". Такие характеристические функции отношений будем называть n -местными предикатами (используются также термины: предикат размерности n, n -арный предикат, предикат валентности n ) и говорить об их истинности или ложности на соответствующих наборах аргументов. Таким образом, предикат - это отображение, сопоставляющее каждому набору своих аргументов одно из логических значений: 1 или 0. Если потребуется, размерность предиката будет указываться соответствующим индексом вверху:P⁽ⁿ⁾ будет означать, что у предиката P имеется n аргументов.

Мы будем рассматривать также функции и предикаты размерности нуль. Множество A⁰ одноэлементно (содержит единственную последовательность длины 0 ). Поэтому функции из A⁰ в A отождествляются с элементами множества A. Такие функции называются константными или просто константами.Предикатов размерности нуль ровно два: 1 (истина) и 0 (ложь).

Вообще говоря, типы объектов-аргументов предиката, т.е. типы множеств A₁, ... , A_n, могут быть различными. Например, у предиката выпускает(Предприятие, Товар), определяющего связь между предприятиями и выпускаемыми ими товарами, первым аргументом является название предприятия, а вторым - одного из выпускаемых им товаров. Но далее для простоты мы будем рассматривать толькопредикаты и функции, все аргументы которых принадлежат одному множеству объектов A. Это ограничение не очень существенно. Можно выделять в A объекты нужных типов с помощью свойств - одноместных предикатов. В нашем случае выражение выпускает(X,Y) можно уточнить, введя предикатыпредприятие⁽¹⁾ и товар⁽¹⁾ и записав конъюнкцию:

.