
- •1.Совершенные нормальные формы.Правила приведения к сднф и скнф. Минимизация логических функций.
- •§8. Нормальные формы функций.
- •8.2 Нормальные формы.
- •8.3 Совершенные нормальные формы.
- •8.4 Правила приведения произвольной формулы алгебры логики к совершенной нормальной форме.
- •8.6 Способ составления снф для произвольной формулы алгебры логики по таблице истинности.
- •§ 1. Понятие формулы исчисления высказываний.
- •§ 2. Определение доказуемой (выводимой) формулы.
- •Правила вывода.
- •Определение выводимой (доказуемой ) формулы.
- •Правило сложной (одновременной) подстановки (спп).
- •Правило сложного заключения.
- •Правило силлогизма.
- •Правило контр позиции.
- •Правило снятия двойного отрицания.
- •§4.Понятие выводимости формул из совокупности формул.
- •§5. Понятие вывода.
- •§6. Правила выводимости.
- •H,w├a из совокупности формул : “Если а выводима из н, то она вы- водима из ”.
- •5. Теорема дедукции: h, c├ a .
- •§9.Проблемы аксиоматического исчисления высказываний.
- •2. Проблема непротиворечивости исчисления высказываний.
- •3.Проблема полноты исчисление высказываний.
- •4.Проблема независимости аксиом исчисления высказываний.
- •§1. Недостаточность логики высказываний. Понятие предиката.
- •§2. Логические операции над предикатами.
- •§3. Кванторные операции.
- •Квантор всеобщности.
- •Квантор существования.
- •Отрицание предложений с кванторами.
- •§4.Понятие формулы логики предикатов.
- •§5. Значение формулы логики предикатов.
- •§6. Равносильные формулы логики предикатов.
- •§7. Нормальные формы формул логики предикатов.
- •§8. Общезначимость и выполнимость формул. Проблема разрешимости.
- •§9. Применение языка логики предикатов для записи математических предложений, определений, построения отрицания предложений.
- •9.1 Запись математических предложений и определений в виде формул логики предикатов.
- •9.2. Построение противоположный утверждений.
- •9.3 Прямая, обратная и противоположная теоремы.
- •9.4 Необходимые и достаточные условия.
- •9.5. Доказательство теорем методом от противного.
- •Утверждения о свойствах объектов и отношениях между ними
- •Язык логики предикатов
- •Синтаксис: формулы логики предикатов
- •Семантика: системы и значения формул на их состояниях
- •Реляционные базы данных
- •Реляционная алгебра
- •Теоретико-множественные операции
- •Специальные реляционные операторы
- •Запросы
- •Ограничения целостности
- •Основные определения
- •Тьюрингово программирование
- •Стандартная заключительная конфигурация
- •Односторонние машины Тьюринга
- •Последовательная и параллельная композиции машин Тьюринга
- •Ветвление (условный оператор)
- •Повторение (цикл)
§9. Применение языка логики предикатов для записи математических предложений, определений, построения отрицания предложений.
9.1 Запись математических предложений и определений в виде формул логики предикатов.
Язык логики предикатов удобен для записи математических предложений и определений. Он дает возможность выражать логические связи между понятиями, записывать определения, теоремы, доказательства. Приведем несколько примеров таких записей.
Пример 1.Определение
предела “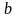 ”
функции ƒ(х), определенной в области E,
в точке x0:
”
функции ƒ(х), определенной в области E,
в точке x0:
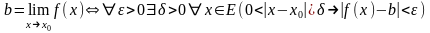 .
Используя трехмесиный предикат
.
Используя трехмесиный предикат
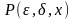 ,
запишем:
,
запишем:
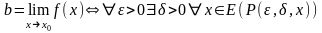 ,
,
где
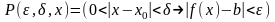 .
.
Пример 2.
Определение непрерывности функции в точке.
Функция
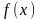 ,
определенная на множестве E,
непрерывна в точке
,
определенная на множестве E,
непрерывна в точке
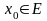 ,
если
,
если
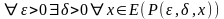 ,
где
,
где
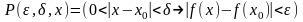 .
.
Пример 3.
Определение возрастающей функции.
Функция
,
определенная на множестве E возрастает
на этом множестве, если
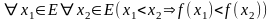 .
.
Здесь использован
двуместный предикат
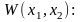
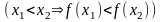 .
.
9.2. Построение противоположный утверждений.
Пусть дано некоторое математическое утверждение А. Ему будет противоположным будет утверждение .
Логика предикатов позволяет путем равносильных преобразований формулы придать ей хорошо обозримый вид.
Определение
неограниченной функции мы получим, беря
отрицание этой формулы и проводя
равносильные преобразования:
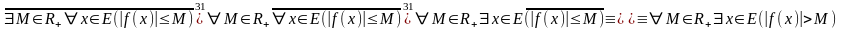 .
.
Последняя формула дает не негативное, а положительное определение неограниченной функции.
Из приведенного определения видно, что для построения противоположного утверждения к утверждению, заданному формулой логики предикатов, содержащей все кванторы впереди, необходимо заменить все кванторы на противоположные и взять отрицание от предиката, стоящего под знаком кванторов.
Особый интерес
представляет построение утверждения,
отрицающего справедливость некоторой
теоремы:
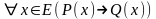 .
Это будет утверждение:
.
Это будет утверждение:
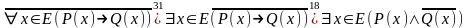 .
.
9.3 Прямая, обратная и противоположная теоремы.
Рассмотрим четыре теоремы:
, (1)
|
|
Пара теорем, у которых условие одной является заключением второй, а условие второй является заключением первой, называются взаимно обратными друг другу.
Так, теоремы (1)и (2), а также (3) и (4)- взаимно обратные теоремы. При этом, если одну из них называют прямой теоремой, то вторая называется обратной.
Пара теорем, у которых условие и заключение одной являются отрицанием соответственно условия и заключения другой, называются взаимно противоположными.
Так, теоремы (1) и (3), а также (2) и (4) являются взаимно противоположными теоремами.
Например, для теоремы “Если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником ” (1) обратной является теорема “Если четырехугольник является прямоугольником, то его диагонали равны” (2). Для теоремы (1) противоположной является теорема “Если в четырехугольнике диагонали не равны, то четырехугольник не является прямоугольником ” (3), а для теоремы (2) противоположной является теорема “Если четырехугольник не является прямоугольником, то его диагонали не равны ” (4).
В рассмотренном примере теоремы (1) и (4) являются одновременно ложными, а теоремы (2) и (3) одновременно истинными. Контрпримером к теореме (1) является равнобочная трапеция.
Ясно, что прямая и обратная теоремы , вообще говоря, не равносильны, т. е. одна из них может быть истинной, а другая – ложной. Однако легко показать, что теоремы (1) и (4), а также (2) и (3) всегда равносильны.
Действительно:
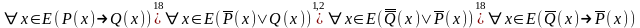 .
.
Из этих равносильностей следует, что, если доказана теорема (1), то доказана и теорема (4), а если доказана теорема (2), то доказана и теорема (3).

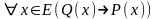 ,
(2)
,
(2)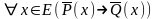 ,
(3)
,
(3)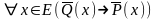 .
(4)
.
(4)