18. Теорема Ролля:

Теорема Ро́лля (теорема о нуле производной) утверждает, что

Если вещественная функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

Геометрический смысл

Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.

Следствие

Если непрерывная функция обращается в ноль в n различных точках, то ее производная обращается в ноль по крайней мере в n − 1 различных точках^[1], причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.

19. Теорема Лагранжа и её геометрический смысл:

 Пусть функция f(x)

1. непрерывна на отрезке [a, b];

2. дифференцируема в интервале (a, b).

Тогда существует точка с  (a, b) такая, что

 

f(b) − f(a) = f '(c) · (b − a) .

(1)

 

Формула (1) называется формулой Лагранжа, или формулой конечных приращений

Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 119.

Геометрическая интерпретация теоремы Лагранжа

Представим формулу (1) в виде

 

f(b) − f(a) b − a    = f '(c) .

(2)

 

Число  

f(b) − f(a)

b − a

   есть угловой коэффициент прямой, проходящей через концы графика функции y = f(x) — точки (a, f(a) ) и (b, f(b) ), а f '(c) — угловой коэффициент касательной к этому графику в точке (c, f(c) ). Из формулы (2) следует, что существует точка с  (a, b), в которой касательная к графику функции f(x) параллельна прямой, проходящей через концы графика (или совпадает с ней) (рис. 2).

20. Теорема Коши и её геометрический смысл

Теорема Коши́ о среднем значении.

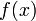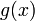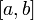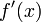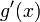Пусть даны две функции   и   такие, что:  и   определены и непрерывны на отрезке  ; производные   и   конечны на интервале 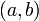 ; производные   и   не обращаются в нуль одновременно на интервале 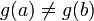 ; тогда 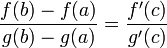, где 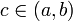 (Если убрать условие 4, то необходимо усилить условие 3: g'(x) не должна обращаться в ноль нигде в интервале (a,b).)

Геометрически это можно переформулировать так: если f и g задают законы движения на плоскости (то есть определяют абсциссу и ординату через параметр t), то на любом отрезке такой кривой, заданном параметрами a и b, найдётся касательный вектор, коллинеарный вектору перемещения от (f(a);g(a)) до (f(b);g(b)).

Доказательство

Для доказательства введём функцию

Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а   равна как раз необходимому числу.