
- •6,7 Электр. И магн. Векторные потенц.Герца
- •11. Поляр-я плоской монохром эм волны
- •19 Нахождение волноводных мод с помощью потенциалов Герца.
- •20 Металлический волновод. Структура э/м поля. Граничные условия.
- •24. Металлический волновод прямоугольного сечения. Структура волны тм поляризации.
- •25.Цилиндрический металлический волновод. Дисперсионное соотношение для волноводных мод те поляризации
- •26,Цилиндрический металлический волновод. Дисперсионное соотношение для волноводных мод тм поляризации
- •30. Погонная индуктивность коаксиального кабеля.
- •31 Решение телеграфных уравнений для коаксиального кабеля.
- •32 Телеграфные уравнения длинной линии с потерями.
- •37 Диаграмма направленности излучения антенны.
- •38 Режимы бегущей и стоячей волн
1.Основные
понятия и математ анализ..
Э\Месть совокупн 2-х физич. величин –
напр-сти э. поля
![]() и м. индукции
и м. индукции
![]()
1). Первый
источник –
это э.заряды Если в обл. находятся э
заряды q,
то вокруг зарядов существует э поле
,
уменьшащ. при удалении от зарядов![]()
![]() В правой части находится ист. поля –
плотность э. заряда .
В левой создаваемое э.поле 2). Второй
источник –
это э.ток. При протекании по проводникам,
вокруг них возникает м.поле
,
которое убывает при удалении от
проводников с током
В правой части находится ист. поля –
плотность э. заряда .
В левой создаваемое э.поле 2). Второй
источник –
это э.ток. При протекании по проводникам,
вокруг них возникает м.поле
,
которое убывает при удалении от
проводников с током
![]() .Если известен вектор плотности э тока
.Если известен вектор плотности э тока
![]() на поверхности S,
то э ток I,
протекающий через эту поверхн. находится
путем интегрир. по этой поверхн..
на поверхности S,
то э ток I,
протекающий через эту поверхн. находится
путем интегрир. по этой поверхн..![]() Здесь
Здесь
![]() ,
где
,
где
![]() -
единичный вектор к поверхности.3). Третий
источник –
это переменное м.поле. Если в обл
пространства существует переменное
м.поле, то в этой обл пространства
появляется э.поле вихревого хар-тера
-
единичный вектор к поверхности.3). Третий
источник –
это переменное м.поле. Если в обл
пространства существует переменное
м.поле, то в этой обл пространства
появляется э.поле вихревого хар-тера
![]() В правой– производная м. поля
В правой– производная м. поля
![]() .
В левой– э.поле
.
Это векторное поле входит в выражение
для ротора поля, что говорит о вихр.
Хар-ре э.поля.4). Четвертый
источник –
это переем.э.поле. Если в обл. пространства
существует переменное э.поле, то в этой
обл. появляется вихревое м.поле.
.
В левой– э.поле
.
Это векторное поле входит в выражение
для ротора поля, что говорит о вихр.
Хар-ре э.поля.4). Четвертый
источник –
это переем.э.поле. Если в обл. пространства
существует переменное э.поле, то в этой
обл. появляется вихревое м.поле.
![]() В правой части– производная э поля по
времени
В правой части– производная э поля по
времени
![]() .
В левой– электр поле
.
Это векторное поле входит в выражение
для ротора поля, что говорит о вихр
хар-ре м.поля. М.объединил все ур в одно
.
В левой– электр поле
.
Это векторное поле входит в выражение
для ротора поля, что говорит о вихр
хар-ре м.поля. М.объединил все ур в одно![]() В правой 2ист.вихревого м.поля-плотность
э.тока и производн.В левой-суммарное
м.поле
В правой 2ист.вихревого м.поля-плотность
э.тока и производн.В левой-суммарное
м.поле
2.Уравнения
Максвелла в дифференциальной
форме.Экспериментальные
и теоре
![]() по теор Гаусса:
по теор Гаусса:![]()
![]() Наличие
div или rot говорит о разной природе
векторного поля. Если rot поля отличен
от нуля, то такое поле вихревое,
в противном случае это безвихревое.
Вихревое поле имеет замкнутые линии
поля, похожие на вихри. Если
Наличие
div или rot говорит о разной природе
векторного поля. Если rot поля отличен
от нуля, то такое поле вихревое,
в противном случае это безвихревое.
Вихревое поле имеет замкнутые линии
поля, похожие на вихри. Если
![]() ,
то линии поля
,
то линии поля
![]() образуют вихрь с направлением вращения
по часовой стрелке, если смотреть вдоль
вектора
образуют вихрь с направлением вращения
по часовой стрелке, если смотреть вдоль
вектора
![]() .
.![]() Если
div поля=0, то такое поле соленоидальное
иначе несоленоид
Линии несоленоид поля
Если
div поля=0, то такое поле соленоидальное
иначе несоленоид
Линии несоленоид поля
![]() начинаются в истоках там где
начинаются в истоках там где
![]() ,
и кончаются в стоках
,
и кончаются в стоках
![]() ,
,
![]() Физ смысл ур М, вх-х в сист:
1-е ур:
источником несоленоид э.поля
Физ смысл ур М, вх-х в сист:
1-е ур:
источником несоленоид э.поля
![]() явл-ся э. заряды с плотностью .”+”(истоки),
а ”-” явл-ся стоками. 2-е
ур:источником
вихревого э.поля
является переменное м.поле
.
3-е ур:м.поле
является соленоид.полемТ.к. в правой
стороне этого ур 0, то у м.поля отсутствуют
истоки и стоки. Т.е отсутствуют + и -. М.
заряды.4-е
ур:ист.
вихревого м.поля
является как э.ток с плотностью
явл-ся э. заряды с плотностью .”+”(истоки),
а ”-” явл-ся стоками. 2-е
ур:источником
вихревого э.поля
является переменное м.поле
.
3-е ур:м.поле
является соленоид.полемТ.к. в правой
стороне этого ур 0, то у м.поля отсутствуют
истоки и стоки. Т.е отсутствуют + и -. М.
заряды.4-е
ур:ист.
вихревого м.поля
является как э.ток с плотностью
![]() ,
так и переменное э.поле
.
Так как 2-ойчлен в правой стороне этого
ур имеет размерность плотности э.тока,
то М. назвал этот член плотностью тока
смещения.
,
так и переменное э.поле
.
Так как 2-ойчлен в правой стороне этого
ур имеет размерность плотности э.тока,
то М. назвал этот член плотностью тока
смещения.
![]() В ур учтена:
В ур учтена:![]() Т.о., линии м.поля всегда замкнуты, а
линии э.поля могут быть как замкнутыми
линиями, так и незамкнутыми. Если э.поле
создается э.зарядами, то линии поля
незамкнуты, они начинаются и кончаются
на э.зарядах. Если же э. поле создается
переменным м.полем, то линии э.поля это
замкнутые вихр. линии.
Т.о., линии м.поля всегда замкнуты, а
линии э.поля могут быть как замкнутыми
линиями, так и незамкнутыми. Если э.поле
создается э.зарядами, то линии поля
незамкнуты, они начинаются и кончаются
на э.зарядах. Если же э. поле создается
переменным м.полем, то линии э.поля это
замкнутые вихр. линии.
3.Уравнения
Максвелла,интегральная форма уравнений.Сист
ур М.имеет вид сист.диф.ур. в частных
производных. Используя т. Гаусса –
Остроградского и Стокса, сист.ур. М в
виде интегральных ур. 1-е
ур
![]() левая сторона равняется по теореме Г.–
О. потоку напряженности э.поля
через замкнутую поверхн S,
охватывающую объем V.
Правая = э.заряду q
в объеме V.
Получим ур.
левая сторона равняется по теореме Г.–
О. потоку напряженности э.поля
через замкнутую поверхн S,
охватывающую объем V.
Правая = э.заряду q
в объеме V.
Получим ур.![]() означающее:Поток напряженности э.поля
через замкнутую поверх. S
равняется э.заряду q
внутри этой поверхности, / на
означающее:Поток напряженности э.поля
через замкнутую поверх. S
равняется э.заряду q
внутри этой поверхности, / на
![]() 2-е ур,
Интегрируем по незамкнутой поверхнS.
2-е ур,
Интегрируем по незамкнутой поверхнS.![]() преобразовывая
преобразовывая![]() Первый интеграл в по т.Стокса= циркуляции
вектора напряженности э.поля
,
по контуру L,
на который натянута поверхность S.В
результате
Первый интеграл в по т.Стокса= циркуляции
вектора напряженности э.поля
,
по контуру L,
на который натянута поверхность S.В
результате![]() означающее:Циркуляция вектора
напряженности э.поля
,
по контуру L,
на который натянута поверхность S,
равна производной по времени от потока
вектора м.индукции
через пов. S,
со знаком минус. Замечая, первый интеграл
, являясь циркуляцией вектора
в
контуре L,
равен электродвижущей силой (ЭДС) e,
действующей в этом контуре. .Правая
сторона ур. является потоком вектора
м.индукции через пов.S,
может быть обозначен как
означающее:Циркуляция вектора
напряженности э.поля
,
по контуру L,
на который натянута поверхность S,
равна производной по времени от потока
вектора м.индукции
через пов. S,
со знаком минус. Замечая, первый интеграл
, являясь циркуляцией вектора
в
контуре L,
равен электродвижущей силой (ЭДС) e,
действующей в этом контуре. .Правая
сторона ур. является потоком вектора
м.индукции через пов.S,
может быть обозначен как
![]() .
В результате ур
.
В результате ур
![]() Изменение потока вектора м.индукции
через поверхность S
натянутую на контур L
вызывает появление ЭДС e
в контуре L.
3-е ур .
Проинтегрируем левую по объему V
и применим теор Г.-О. Получим
Изменение потока вектора м.индукции
через поверхность S
натянутую на контур L
вызывает появление ЭДС e
в контуре L.
3-е ур .
Проинтегрируем левую по объему V
и применим теор Г.-О. Получим
![]() означающее:поток
вектора м.индукции
через произвольную замкнутую пов.S
равен 0. Т.е., сколько линий магнитного
поля входит в замкнутую поверхность S,
столько же линий выходит из этой
поверхностиТ.е. м.поле – это соленоид.поле
4-ое ур
.Интегрируем по поверхн S.
означающее:поток
вектора м.индукции
через произвольную замкнутую пов.S
равен 0. Т.е., сколько линий магнитного
поля входит в замкнутую поверхность S,
столько же линий выходит из этой
поверхностиТ.е. м.поле – это соленоид.поле
4-ое ур
.Интегрируем по поверхн S.![]() 2-ой интеграл является э.током I,
текущим через поверх. S.
В рез..
2-ой интеграл является э.током I,
текущим через поверх. S.
В рез..![]() означает: Циркуляция вектора м.индукции
по произвольному контуру L
отлична от нуля в двух случаях. Во-первых,
течет э.ток I,
который охватывается контуром L.
Во-вторых, если поток напряженности
э.поля
через поверхность S,
натянутую на контур L,
меняется со временем.
означает: Циркуляция вектора м.индукции
по произвольному контуру L
отлична от нуля в двух случаях. Во-первых,
течет э.ток I,
который охватывается контуром L.
Во-вторых, если поток напряженности
э.поля
через поверхность S,
натянутую на контур L,
меняется со временем.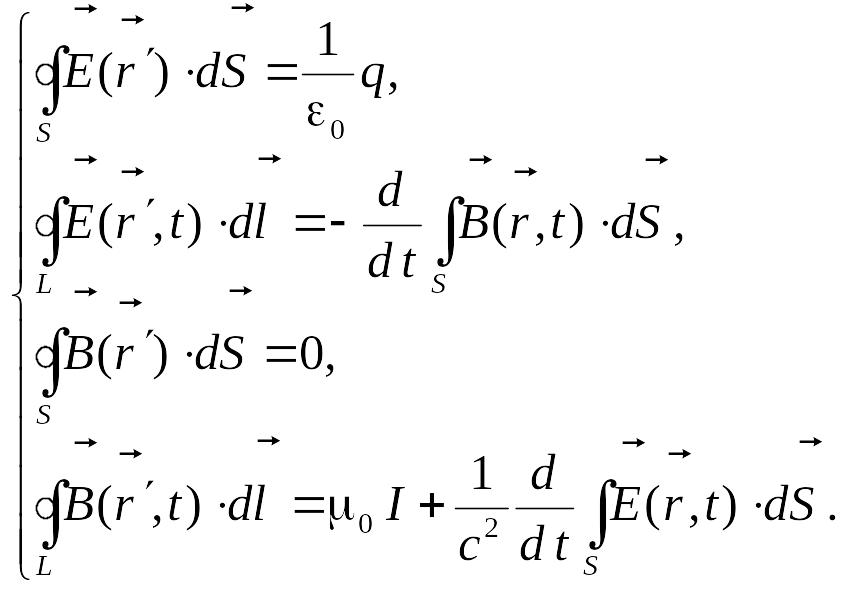
4,5
Потенциалы
электромагнитного поля. Калибровочная
инвариантность. Калибровка Лоренца.Вместо
векторов э.и магнитно поля
![]() ,
вводят вспомогательные поля
,
вводят вспомогательные поля
![]() .
Векторное поле
.
Векторное поле
![]() называется
векторным потенциалом,
а скалярное поле
называется
векторным потенциалом,
а скалярное поле
![]() скалярным
потенциалом.
Вектор
и
,
выражаются через векторный потенциал
и скалярный потенциал
скалярным
потенциалом.
Вектор
и
,
выражаются через векторный потенциал
и скалярный потенциал
![]() так.
так.
![]() В сист. Ур. М
В сист. Ур. М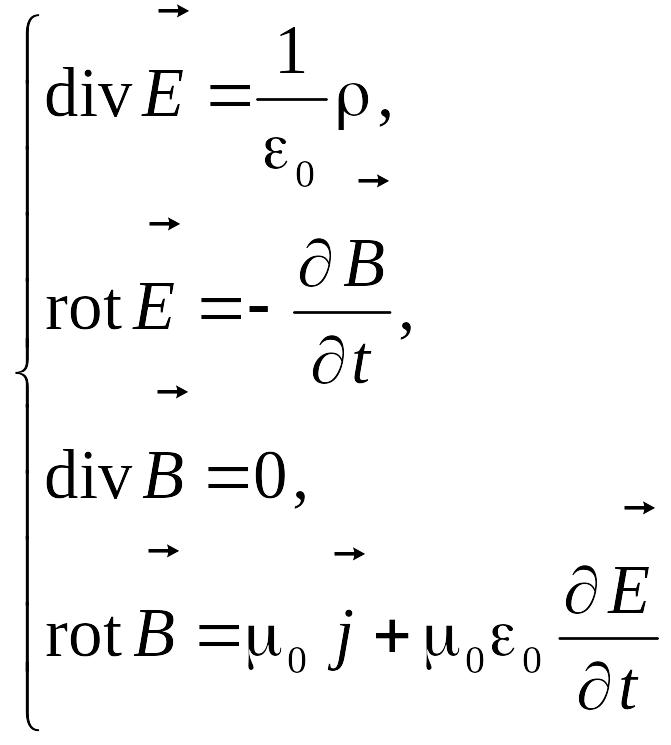 .
Подставим это во 2-е ур. Сист..Получим
.
Подставим это во 2-е ур. Сист..Получим
![]() Раскроем
скобки
Раскроем
скобки![]() Т.к.
rot*grad
скалярного поля всегда равен 0, то
ур.превращается в тождество 0 = 0 Подставим
преобразов. в третье ур. Сист.В результате.
Т.к.
rot*grad
скалярного поля всегда равен 0, то
ур.превращается в тождество 0 = 0 Подставим
преобразов. в третье ур. Сист.В результате.![]() Т.к.для векторного поля див. Рот. равна
нулю, ур. превращается в тождество 0 = 0.
Поэт 3-е ур. выполняется подстановкой и
его не нужно рассматривать
дальше.Т.о.,получаем сист.
Т.к.для векторного поля див. Рот. равна
нулю, ур. превращается в тождество 0 = 0.
Поэт 3-е ур. выполняется подстановкой и
его не нужно рассматривать
дальше.Т.о.,получаем сист.
 Учли связь .
Учли связь .
![]() Вспомним,
Вспомним,
![]() ,
где
оператор Лапласа.Выражение
,
где
оператор Лапласа.Выражение![]() .Учитывая соотношения:
.Учитывая соотношения: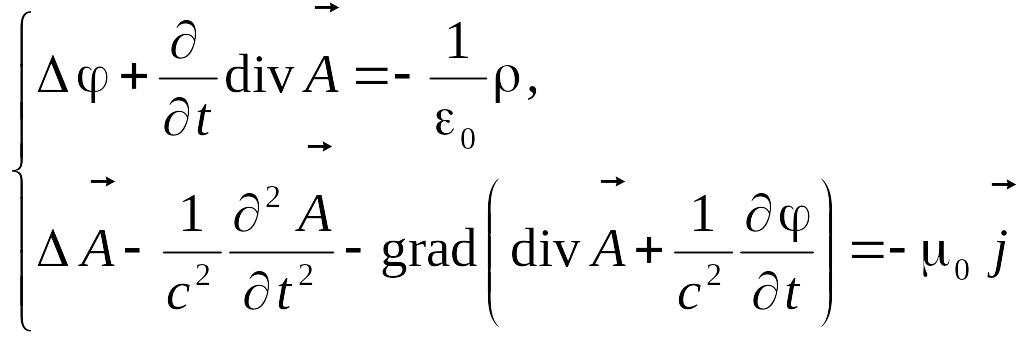 . является системой 4-х
диф.ур.. Для 4-х неизвестных функций
. является системой 4-х
диф.ур.. Для 4-х неизвестных функций![]() Рассмотрим два набора э/м потенциалов
Рассмотрим два набора э/м потенциалов
![]() и
и
![]() .
связаны друг с другом
.
связаны друг с другом
![]() где
f
- произвольная функция координат и
времени. Покажем, что поля
где
f
- произвольная функция координат и
времени. Покажем, что поля
![]() найденные с помощью потенциалов
и поля найденные с пом. Пот.
совпадают. Т.е, измен. э/м. потенц.
найденные с помощью потенциалов
и поля найденные с пом. Пот.
совпадают. Т.е, измен. э/м. потенц.
![]() не приводит к изменению векторов
э/м поля. Такое поведение полей называется
градиентной
или калибровочной инвариантностью.Эта
неоднозначность в выборе электромагнитных
потенциалов позволяет накладывать на
потенциалы дополнительные условия.
Такие дополнительные условия называются
калибровками.
Калибровка
Лоренца
задается:
не приводит к изменению векторов
э/м поля. Такое поведение полей называется
градиентной
или калибровочной инвариантностью.Эта
неоднозначность в выборе электромагнитных
потенциалов позволяет накладывать на
потенциалы дополнительные условия.
Такие дополнительные условия называются
калибровками.
Калибровка
Лоренца
задается:
![]() Подставляя это получ
Подставляя это получ
![]()
Калибровка Кулона
задается:![]() подставляя в сист получаем
подставляя в сист получаем![]() .
.
6,7 Электр. И магн. Векторные потенц.Герца
Считая, что сист
ист. э/м поля эл-ки нейтральна, т.е.
![]() , где V–объем
занимаемый сист ист. поля. За-н сохр.
Э.заряда
, где V–объем
занимаемый сист ист. поля. За-н сохр.
Э.заряда
![]() Эти усл-я будут вып-ся, если вв в-р
э.пол-ции
Эти усл-я будут вып-ся, если вв в-р
э.пол-ции
![]() и в-р намаг-и
:
и в-р намаг-и
:![]() .
В-ры
.
В-ры
![]() опр-ся
неодн-но
опр-ся
неодн-но![]() где
где
![]() –
произвольный вектор и скаляр, не изм.т
физ-х вел-н
–
произвольный вектор и скаляр, не изм.т
физ-х вел-н
![]() в соотн-ии Будем считать, что
–
э.дип-й момент ед-ы объема, а
–
м. дип-й м-т ед. объема. Обозн-м
в соотн-ии Будем считать, что
–
э.дип-й момент ед-ы объема, а
–
м. дип-й м-т ед. объема. Обозн-м
![]() -
э. дип. м-т эл-та объема dV,
а через
-
э. дип. м-т эл-та объема dV,
а через
![]() -
м.дип-й м-т эл-та объема
dV, то:
-
м.дип-й м-т эл-та объема
dV, то:
![]() Эдля
сист.
Эдля
сист.
![]() т.е
т.е![]() Рассмотрим сист, которая характеризуется
вектором э.поляризации
,
а
Рассмотрим сист, которая характеризуется
вектором э.поляризации
,
а
![]() .
Тогда
.
Тогда![]() Используя ур. для э/м потенциалов с
калибровкой Лоренца т.е
Используя ур. для э/м потенциалов с
калибровкой Лоренца т.е![]() Для выполнения колибровки, вв
Для выполнения колибровки, вв
![]() Подстановка этого
Подстановка этого
![]() в
1-е и 2-е ур сист, приводит к
в
1-е и 2-е ур сист, приводит к
![]() Получаем
формулы,
через э.вектор Герца
.
Получаем
формулы,
через э.вектор Герца
.![]() Рассмотрим сист, характеризуется
вектором намагниченности
,
а вектор э.поляризации этой системы
равен нулю
Рассмотрим сист, характеризуется
вектором намагниченности
,
а вектор э.поляризации этой системы
равен нулю
![]() .
Тогда соотношения:
.
Тогда соотношения:![]() Здесь
за-н сохранения заряда выполняется:
Здесь
за-н сохранения заряда выполняется:
![]() Используем
ур для э/м потенциалов с калибровкой
К..
Используем
ур для э/м потенциалов с калибровкой
К..
![]() Вводим
Вводим![]() :
:![]() Подстановка для
в 1-е и 2-е ур сист, приводит к
Подстановка для
в 1-е и 2-е ур сист, приводит к
![]() получаем
.
получаем
.![]() .Рассмотрим поле вне источников т.е .
.Рассмотрим поле вне источников т.е .
![]() .
Тогда ур. принимают вид волнового
ур.
.
Тогда ур. принимают вид волнового
ур.
![]() НО э.
и м.
векторы Герца имеют разную геометрическую
природу:1)ист. для э. вектора Герца
служит вектор э.поляризации
,являющийся
полярным вектором, поэтому э. вектор
Герца тоже является полярным. Ист для
м.вектора Герца
служит вектор намаг-ти
являющийся
аксиальным, поэтому м.в-р Герца тоже
является акс-м.2) Э.поле представимо в
виде:
НО э.
и м.
векторы Герца имеют разную геометрическую
природу:1)ист. для э. вектора Герца
служит вектор э.поляризации
,являющийся
полярным вектором, поэтому э. вектор
Герца тоже является полярным. Ист для
м.вектора Герца
служит вектор намаг-ти
являющийся
аксиальным, поэтому м.в-р Герца тоже
является акс-м.2) Э.поле представимо в
виде:![]()
![]()
![]() поле Е1-векторное,
поле Е1-векторное,![]() –
соленоидальное.Если
–
соленоидальное.Если
![]() то
то
![]() -
гармоническое.Если
-
гармоническое.Если![]() то
-вихревое.Т.о.
э.поле состоит из потенциальных поле и
вихревых.
определяет
только вихревые поля
определяет
потенциальные, так и вихревые поля.
то
-вихревое.Т.о.
э.поле состоит из потенциальных поле и
вихревых.
определяет
только вихревые поля
определяет
потенциальные, так и вихревые поля.
8.9Уравнение
баланса энецргии электромагнитного
поля.Возьмем
сист. Ур. М.
![]() Далее
в сист. (4)-(2),
Далее
в сист. (4)-(2),
![]() вычислим
вычислим![]() Рассмотрим
Рассмотрим
![]() тогда.
тогда.![]() Вв обозначения.
Вв обозначения.![]() здесь w – плотность энергии э/мполя.Если
известна w
вобъеме V,
то энергия э/м поля W
в этом объеме
здесь w – плотность энергии э/мполя.Если
известна w
вобъеме V,
то энергия э/м поля W
в этом объеме
![]() Вв.обозначение
Вв.обозначение![]() где
где![]() имеет размерность Дж/м2/с,
и называется вектором Пойн.его физич.
смысл:это есть вектор плотности потока
энергии.
имеет размерность Дж/м2/с,
и называется вектором Пойн.его физич.
смысл:это есть вектор плотности потока
энергии.
![]() показывает
какая энергия переноситься через единицу
поверхности в единицу времени.В результате
показывает
какая энергия переноситься через единицу
поверхности в единицу времени.В результате
![]() это уравнение
баланса энергии
э/м поля.после интегриров.
это уравнение
баланса энергии
э/м поля.после интегриров.![]() Физич смысл:левая сторона, обозначает
уменьшение энергии электромагнитного
поля W
в объеме V
в единицу времени. Справа описываются
процессы, за счет которых уменьшается
энергия э/мполя. Т.к, часть энергии идет
на работу э.поля над движущимися зарядами
в объеме V.
Мощность P,
выделяемая при этом в объеме V
будет равна.
Физич смысл:левая сторона, обозначает
уменьшение энергии электромагнитного
поля W
в объеме V
в единицу времени. Справа описываются
процессы, за счет которых уменьшается
энергия э/мполя. Т.к, часть энергии идет
на работу э.поля над движущимися зарядами
в объеме V.
Мощность P,
выделяемая при этом в объеме V
будет равна.
![]() Во-вторых,
часть энергии уносится через поверхность
S,
окружающую этот объем в виде э/м излучения.
Поток энергии
Во-вторых,
часть энергии уносится через поверхность
S,
окружающую этот объем в виде э/м излучения.
Поток энергии
![]() через эту поверхность будет равен.
через эту поверхность будет равен.![]() Теперь ур.баланса
Теперь ур.баланса
![]()
10,Среднее
значение плотности энергии и вектора
Пойтинга для монохроматического ЭМ
поля
–
это вектор плотности потока энергии
э/м поля![]() где
и
– это действительные векторные
поляРассмотр.монохроматические поля.
В комплек..
где
и
– это действительные векторные
поляРассмотр.монохроматические поля.
В комплек..![]()
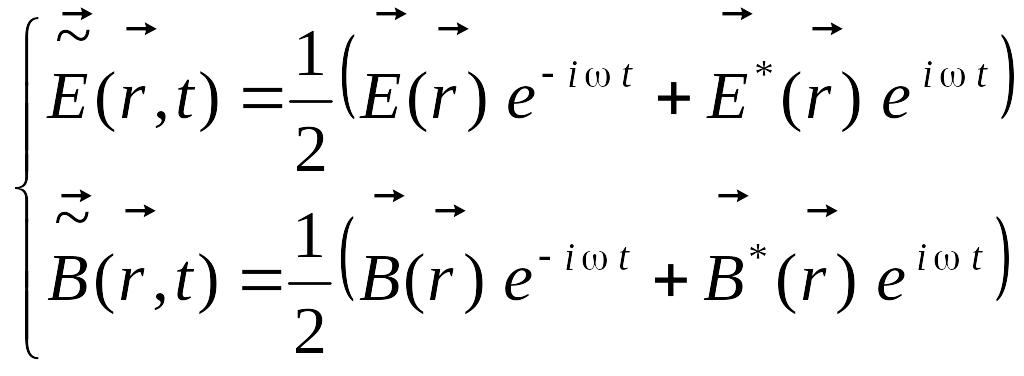
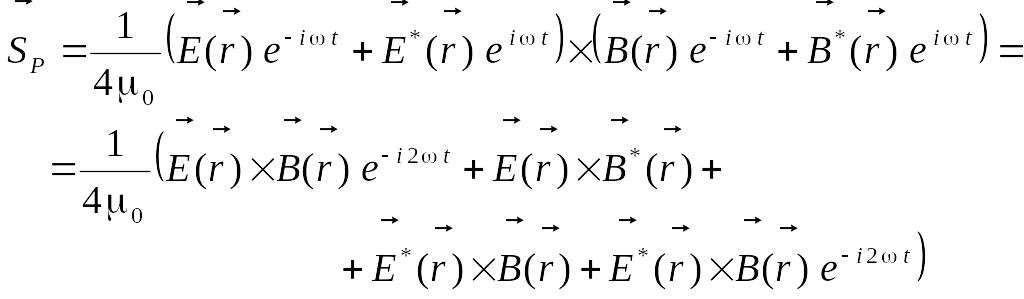 Рассмотрим усреднение
Рассмотрим усреднение
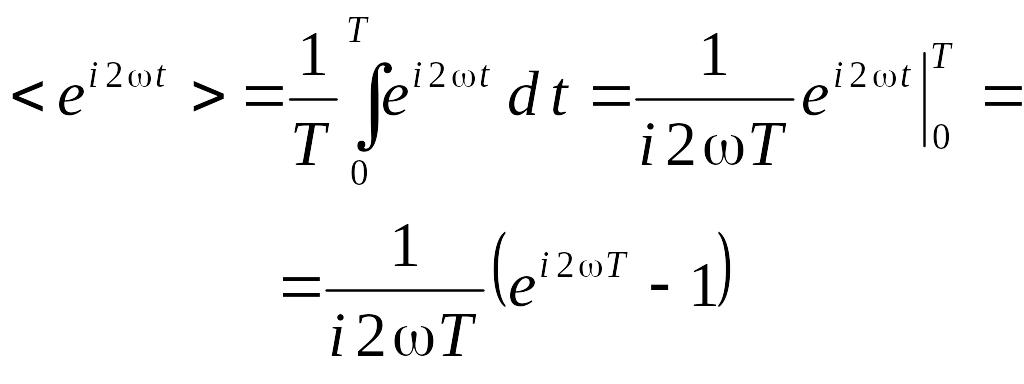 В результате получаем
В результате получаем
![]() Подставляем в формулу и Взяв компл.
сопряжение от обеих частей
Подставляем в формулу и Взяв компл.
сопряжение от обеих частей
![]() Теперь
производим усреднение
Теперь
производим усреднение
![]() В
результате для монохромат волны
В
результате для монохромат волны
![]()
