6*. Неоднакове число випробувань на різних рівнях

Нами передбачалось, що число випробувань на різних рівнях є однаковим. Нехай число випробувань на різних рівнях, взагалі кажучи, різне, а саме: проведено випробувань на рівні , випробувань – на рівні , , випробувань – на рівні . В цьому випадку загальну суму квадратів відхилень знаходять за формулою

,

де 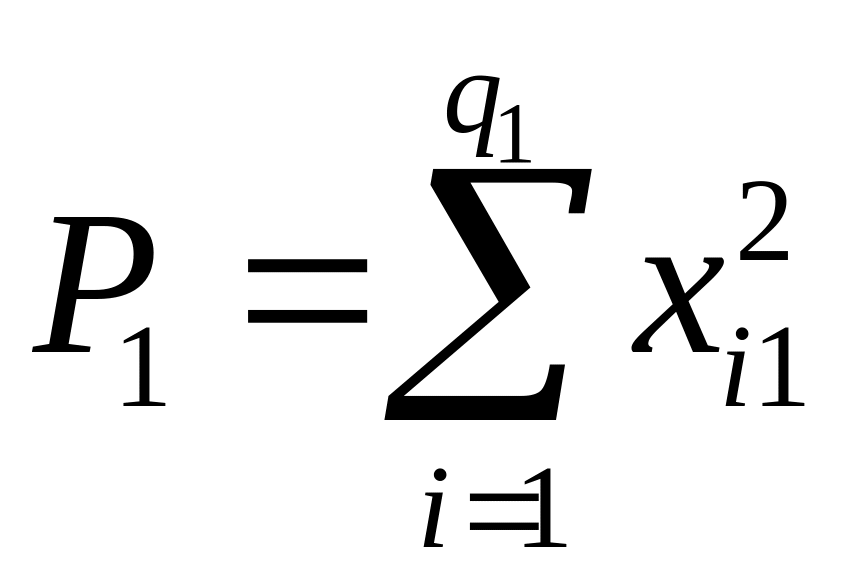– сумма квадратів спостерігаємого значення ознаки на рівні ;

– сумма квадратів спостерігаємого значення ознаки на рівні ;

– сумма квадратів спостерігаємого значення ознаки на рівні ;

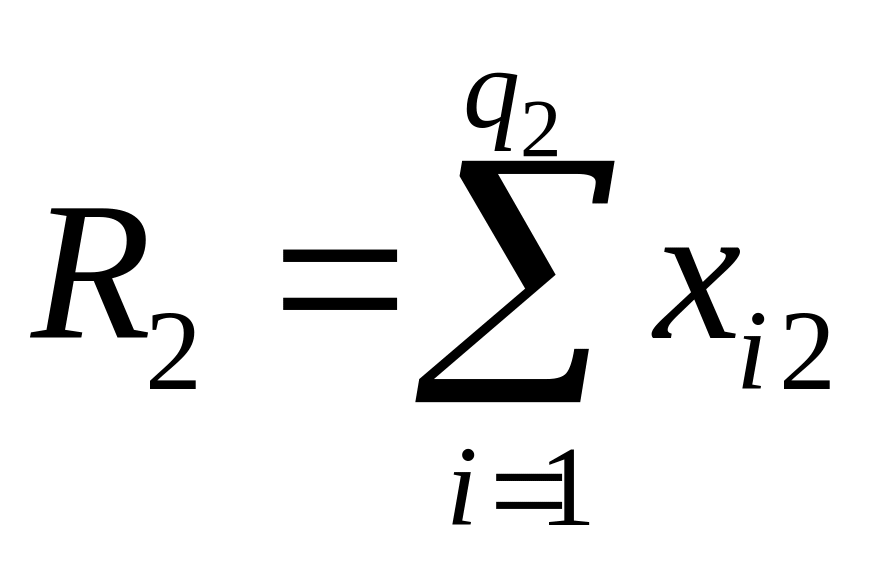, , , – суми значень ознаки, що спостерігалися, відповідно на рівнях , , , ;

– загальне число випробувань (об’єм вибірки).

Якщо для спрощення обчислень з кожного значення , що спостерігалося, віднімали одне і те ж число , то

,

де , , , ; , , , .

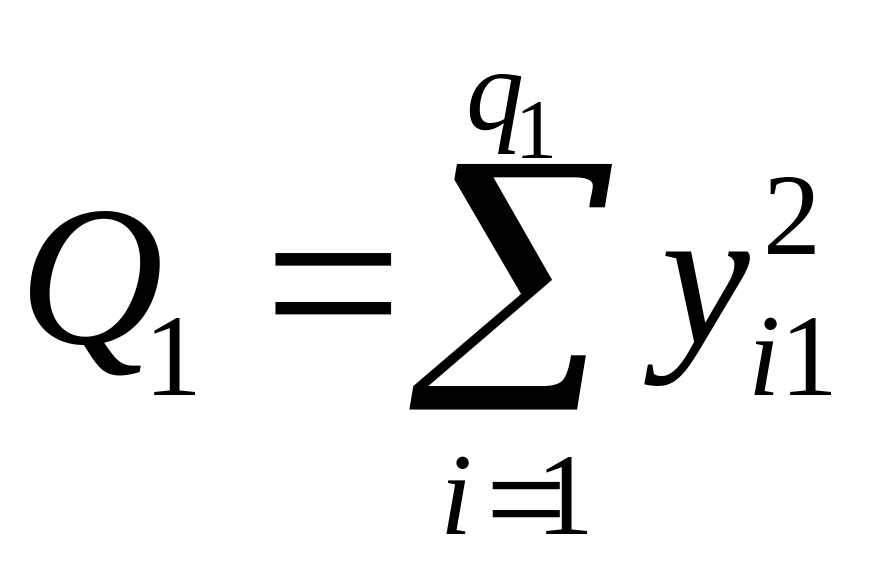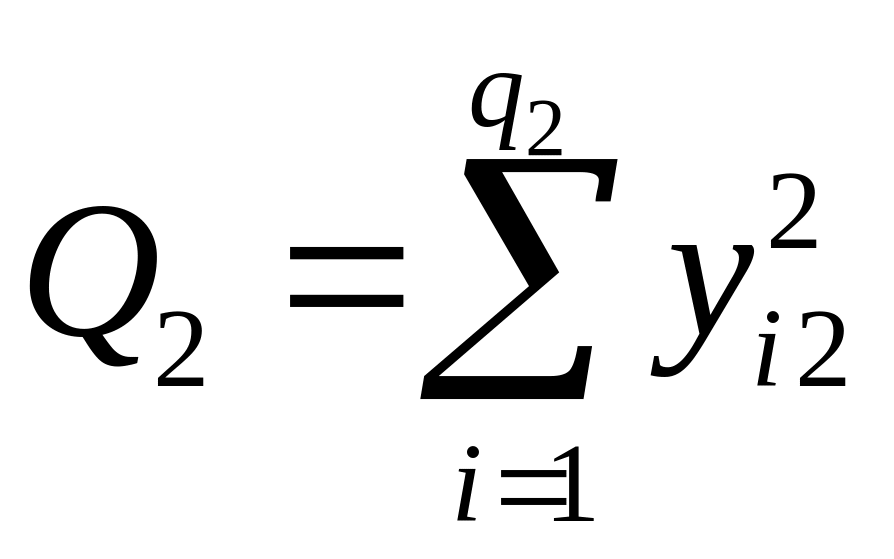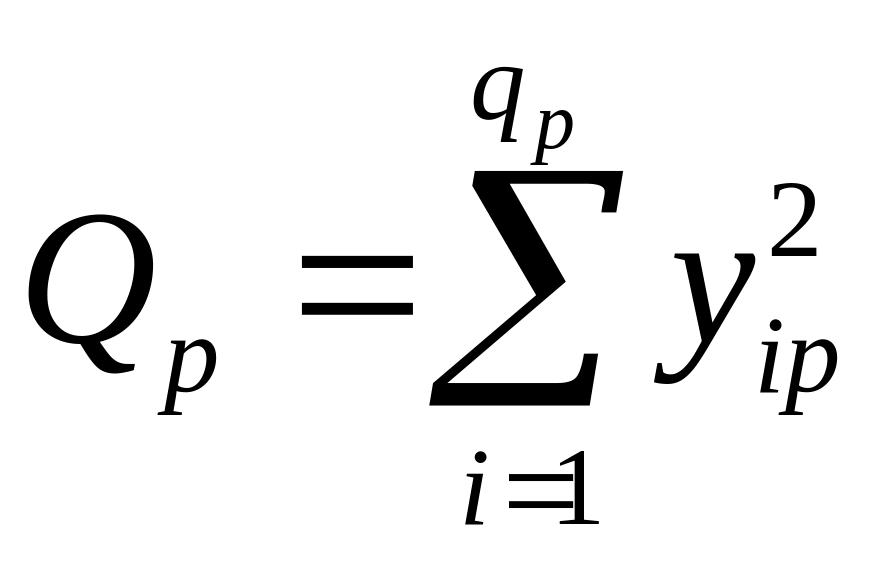Факторну суму квадратів відхилень знаходять за формулою

;

якщо значення ознаки були зменшені , то

.

Решту обчислень проводять, як і у разі однакового числа випробувань:

,

, .

Приклад. Проведено випробувань, з них на першому рівні фактора, – на другому і – на третьому. Результати випробувань приведены в таблиці. Методом дисперсійного аналізу при рівні значущості перевірити нульову гіпотезу про рівність групових середніх. Передбачається, що вибірки витягнуті з нормальних совокупностей з однаковими дисперсіями.

Номер випробування	Рівні фактора

Розв’язання. Для спрощення розрахунку віднімемо з кожного спостережуваного значення: . Складемо розрахункову таблицю.

Використовуючи таблицю, знайдемо загальну і факторну суми квадратів відхилень:

;

.

Знайдемо залишкову суму квадратів відхилень:

.

Знайдемо факторну і залишкову дисперсії:

;

.

Порівняємо факторну і залишкову дисперсії за критерієь , для чого знайдемо спостережуване значення критерію:

.

Номер випробування	Рівні фактора						Підсумковий стовпець

Враховуючи, що число ступенів свободи чисельника , а знаменника і рівень значущості , по таблиці додатку знаходимо критичну точку: .

Оскільки – нулевую гіпотезу про рівність групових середніх відкидаємо. Іншими словами, групові середні розрізняються значущо.

12