3*. Зв’язок між загальною, факторною і залишковою сумами

Покажемо, що

Для спрощення висновку обмежимося двома рівнями і двома випробуваннями на кожному рівні . Результати випробувань представимо у вигляді таблиці.

Номер випробування	Рівні фактора

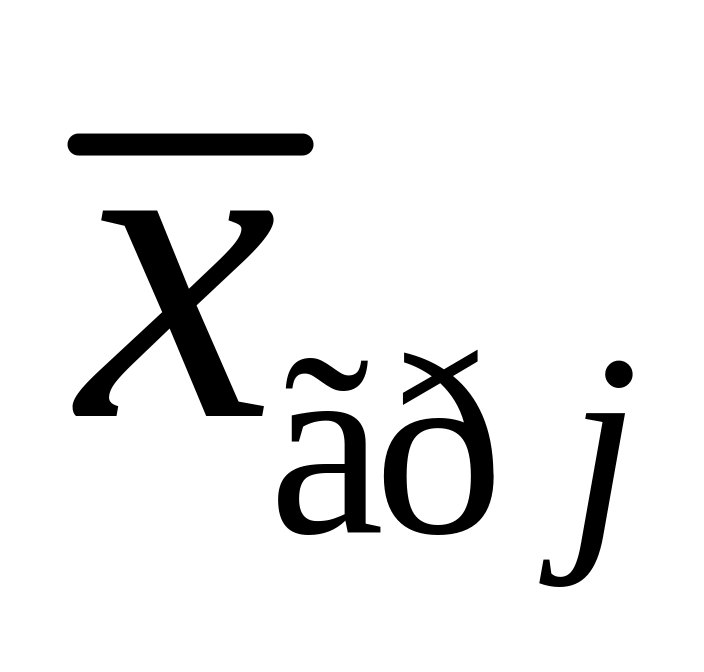
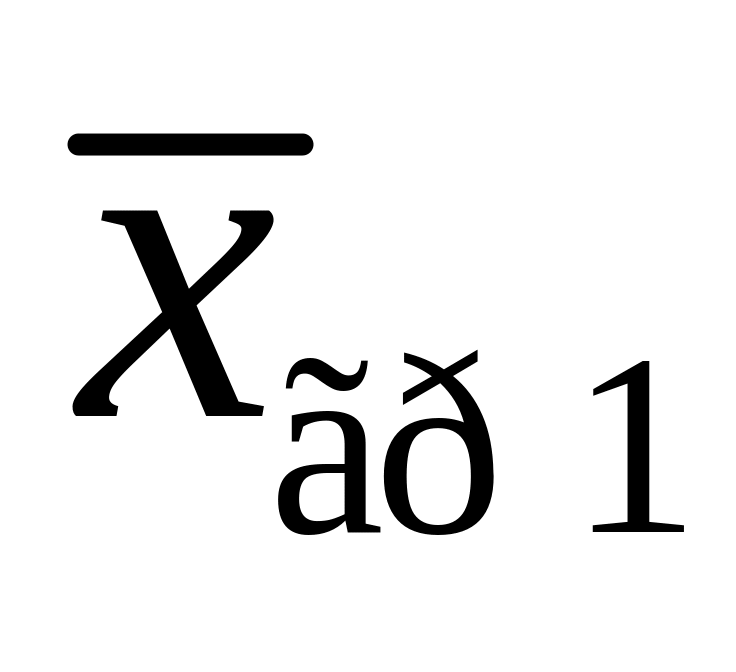
Тоді

.

Віднімемо і додамо до кожного спостережуваного значення на першому рівні групову середню , а на другому – . Виконавши підведення до квадрату і враховуючи, що сума всіх подвоєних добутків дорівнює нулю, отримаємо

.

Отже,

.

Слідство. З отриманої рівності витікає важливе слідство:

.

Звідси видно, що немає потреби безпосередньо обчислювати залишкову суму: достатньо знайти загальну і факторну суми, а потім їх різницю.

4*. Загальна, факторна і залишкова дисперсії

Розділивши суми квадратів відхилень на відповідне число ступенів свободи, отримаємо загальну, факторну і залишкову дисперсії:

, , ,

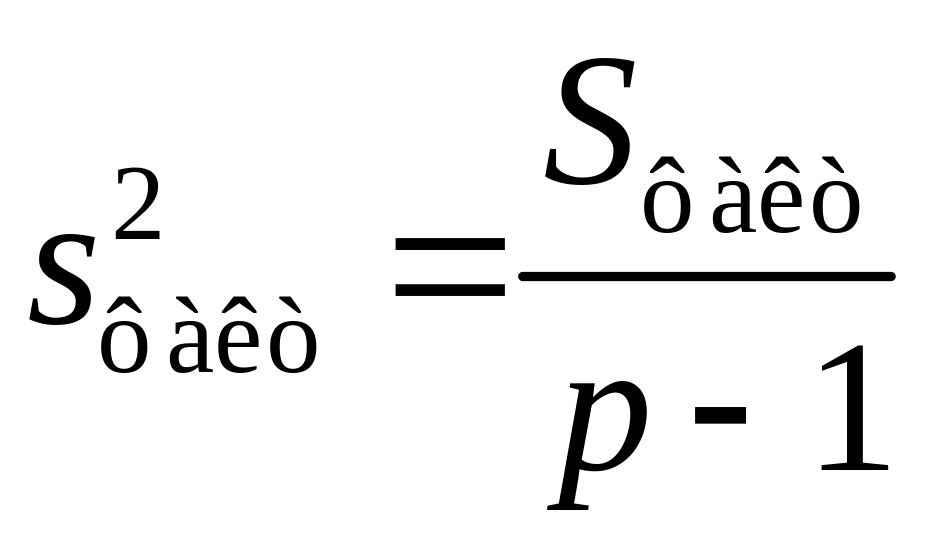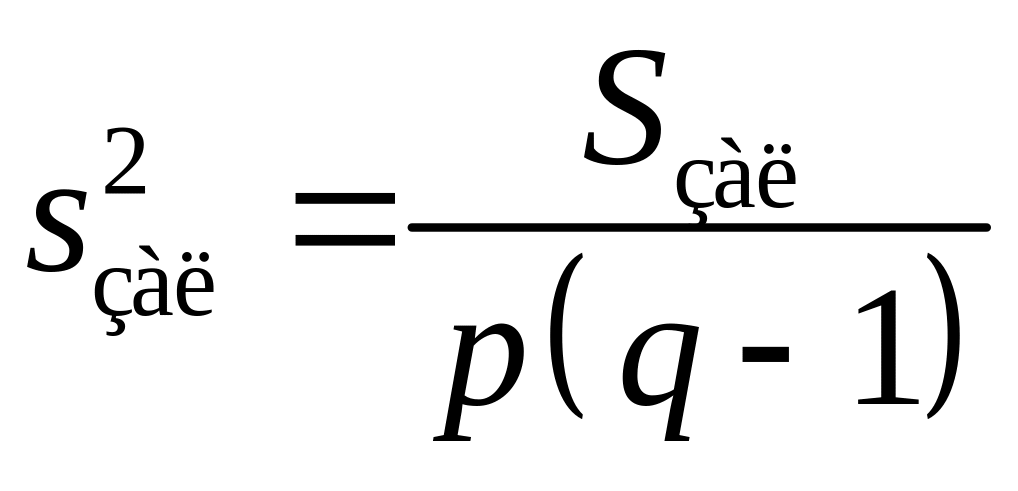де – число, рівнів фактора; – число спостережень на кожному рівні; – число степенів свободи загальної дисперсії; – число степенів свободи факторної дисперсії; – число степенів свободи залишкової дисперсії.

Якщо нульова гіпотеза про рівність середніх справедлива, то всі ці дисперсії є незміщеними оцінками генеральної дисперсії. Наприклад, враховуючи, що об’єм вибірки укладаємо, що

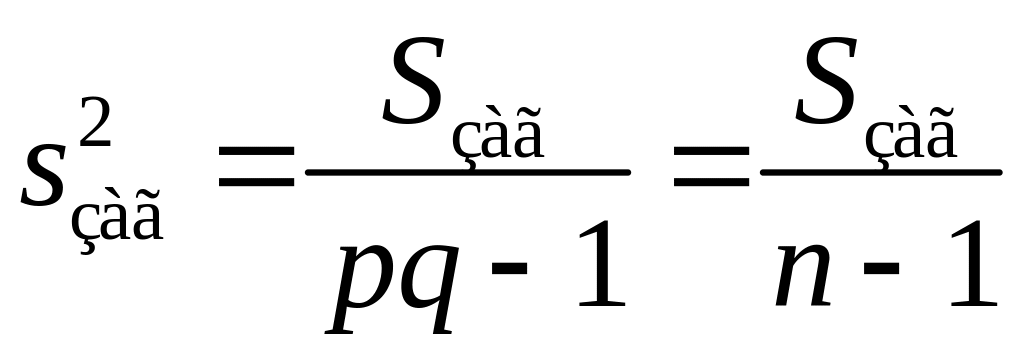
– виправлена вибіркова дисперсія, яка, як відомо, є незміщеною оцінкою генеральної дисперсії.

Зауваження. Число степенів свободи залишкової дисперсії дорівнює різниці між числами степенів свободи загальної і факторної дисперсій. Дійсно

.

5*. Порівняння декількох середніх методом дисперсійного аналізу

Треба перевірити при заданому рівні значущості нульову гіпотезу про рівність декількох середніх нормальних сукупностей з невідомими, але однаковими дисперсіями. Покажемо, що розв’язок цієї задачі зводиться до порівняння факторної і залишкової дисперсій по критерію Фишера – Снедекора.

1. Нехай нульова гіпотеза про рівність декількох середніх (надалі називатимемо їх груповими) правильна. В цьому випадку факторна і залишкова дисперсії є незміщеними оцінками невідомої генеральної дисперсії і, отже, розрізняються незначущо. Якщо порівняти ці оцінки по критерію , то очевидно, критерій вкаже, що нульову гіпотезу про рівність факторної і залишкової дисперсій слід прийняти.

Таким чином, якщо гіпотеза про рівність групових середніх правильна, то вірна і гіпотеза про рівність факторної і залишкової дисперсій.

2. Нехай нульова гіпотеза про рівність групових середніх помилкова. В цьому випадку із зростанням расхождения між груповими середніми збільшується факторна дисперсія, а разом з нею і відношення . У результаті виявиться більше і, отже, гіпотеза про рівність дисперсій буде знехтувана.

Таким чином, якщо гіпотеза про рівність групових середніх помилкова, то помилкова і гіпотеза про рівність факторної і залишкової дисперсій.

Легко довести від протилежного справедливість зворотних тверджень: з правильності (помилковості) гіпотези про дисперсії слідує правильність (помилковість) гіпотези про середні.

Отже, для того, щоб перевірити нульову гіпотезу про рівність групових середніх нормальних совокупностей з однаковими дисперсіями, достатньо перевірити по критерію нульову гіпотезу про рівність факторної ізалишкової дисперсій. В цьому і полягає метод дисперсійного аналізу.

Зауваження 1. Якщо факторна дисперсія виявиться менше залишкової, то вже звідси слідує справедливість гіпотези про рівність групових середніх і, значить, немає потреби вдаватися до критерію .

Зауваження 2. Якщо немає впевненості в справедливості предположення про рівність дисперсій розглядаваних сукупностей, то це припущення слід перевірити заздалегідь, наприклад по критерію Кочрена.

Приклад. Проведено по випробування на кожних з трьох рівнів. Результати випробувань приведені в таблиці. Методом дисперсійного аналізу при рівні значущості перевірити нульову гіпотезу про рівність группорых середніх. Передбачається, що вибірки витягнуті з нормальних

Номер випробування	Рівні фактора

совокупностей з однаковими дисперсіями.

Розв’язання. Для спрощення розрахунку віднімемо з кожного спостережуваного значення: . Складемо розрахункову таблицю.

Користуючись таблицею і враховуючи, що число рівнів фактора , число випробувань на кожному рівні , знайдемо загальну і факторну суми квадратів відхилень:

;

.

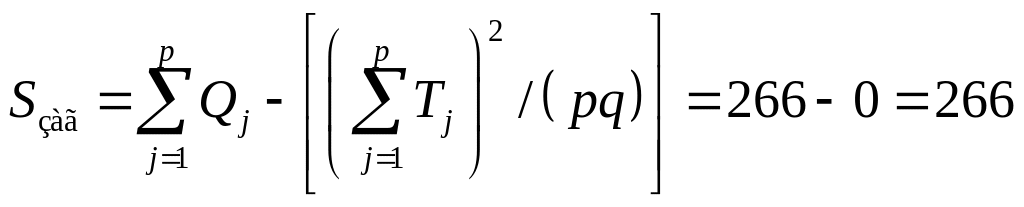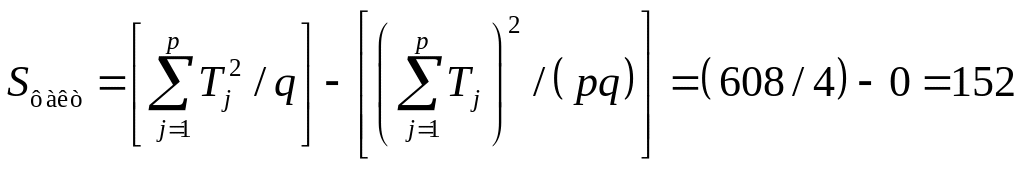Знайдемо залишкову суму квадратів відхилень:

.

Знайдемо факторну і залишкову дисперсії:

;

Номер випробування	Рівні фактора						Підсумковий стовпець

.

Порівняємо факторну і залишкову дисперсії по критерію , для чого знайдемо спостережуване значення критерію:

.

Враховуючи, що число ступенів свободи чисельника , а знаменника і рівень значущості , по таблиці знаходимо критичну точку:

.

Оскільки – нулевую гіпотезу про рівність групових середніх відкидаємо. Іншими словами, групові середні «в цілому» розрізняються значущо. Якщо вимагається порівняти середні попарно, то слід скористатися критерієм Стьюдента.

Зауваження 3. Якщо спостережувані значення – десяткові дроби з одним знаком після коми, то доцільно перейти до чисел , де – приблизно середнє значення чисел . В підсумку отримаємо порівняно невеликі цілі числа. Хоча при цьому факторна і залишкова дисперсія збільшуються в разів, їх відношення не зміниться. Наприклад; якщо , , , то, прийнявши , отримаємо: , , .

Аналогічно поступають, якщо після коми є знаків:

.