3*. Класифікація станів і ланцюгів Маркова

Властивості ланцюга Маркова та відповідно способи розв’язання пов’язаних з його аналізом задач істотно залежать від того, з яких саме станів він складається. У зв’язку з цим наведемо тут прийняту класифікацію станів скінченого ланцюга Маркова та обумовлену нею класифікацію самих ланцюгів Маркова.

Означення. Кажуть, що стан досягається зі стану якщо існує таке число кроків , що , тобто з додатною ймовірністю ланцюг Маркова за кроків переходить із стану в стан (включаючи випадок ).

У термінах ймовірностей першого досягнення той факт, що стан досягається зі стану може бути визначений умовою . Повертаючись до наших прикладів, можна легко переконатися в тому, що в прикладах 7, 9 всі стани розглядуваних там ланцюгів Маркова є досяжними з будь-яких станів, а в прикладі 8 всі стани досягаються зі станів .

Означення. Множина станів називається поглинаючою (або замкненою), якщо кожний стан, який не входить в , є недосяжний з жодного стану, який належить , тобто, коли для всіх та таких, що належить , а не належить.

Звідси, зокрема, випливає, що окремий розгляд станів, які входять у замкнену множину, знову приводить до ланцюга Маркова, який можна вивчати незалежно.

Якщо один стан утворює замкнену множину, то він називається поглинаючим станом. Наприклад, стани та у прикладі 8 є поглинаючими.

Означення. Стан і називається зворотним, якщо ймовірність повернення для нього дорівнює одиниці, тобто , і незворотним, якщо ця ймовірність менша від одиниці, тобто .

Можна показати, що стан ланцюга Маркова є зворотним тоді і тільки тоді, коли середнє число повернень в нього нескінченне, і що з будь-якого зворотного стану не можна досягнути жодного незворотного стану. Крім цього, для того, щоби стан був незворотним необхідно і достатньо, щоб .

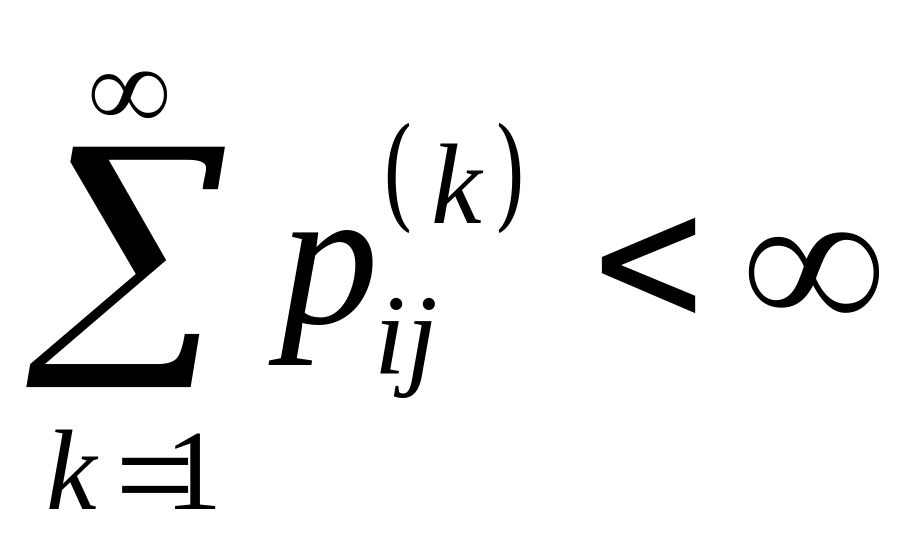Означення. Стан називається періодичним з періодом , якщо , коли не є кратним , і – найбільше ціле число з цією властивістю (тобто система не може повернутися в стан за час, відмінний від . Стан називається неперіодичним, якщо такого не існує.

Означення. Стан і називається ергодичним, якщо він зворотний і неперіодичний.

Наведені означення різних типів станів марковського ланцюга становлять основу класифікації самих ланцюгів Маркова.

Означення. Ланцюг Маркова називається незвідним, якщо він не містить замкнених множин станів, відмінних від множини всіх станів.

З даного означення випливає, що незвідний скінченний ланцюг Маркова складається лише із зворотних станів, кожний з яких досягається з будь-якого іншого стану ланцюга. Отже, виходячи з означення замкненої (поглинаючої) множини станів, робимо висновок, що будь-яка така множина може розглядатися як незвідний скінченний ланцюг Маркова.

Означення. Ланцюг Маркова називається ергодичним, якщо він незвідний і всі його стани є ергодичними.

Властивість ергодичності для однорідного ланцюга Маркова в термінах перехідних ймовірностей означає, що існує таке ціле число , що всі елементи матриці є додатними.

Зауважимо, що при аналізі структури ланцюга Маркова слід розрізняти визначене вище поняття поглинаючої (замкненої) множини станів від множини поглинаючих станів. Очевидно, в останньому випадку ланцюг Маркова вже не може бути незвідним, оскільки не всі стани є взаємодосяжними (з поглинаючого стану жодний інший стан не досягається). Зрозуміло також, що такий ланцюг мусить містити незворотні стани, бо якщо поглинаючий стан є досяжним для деякого стану , то система вже не може повернутися в стан з ймовірністю одиниця (а тому стан незворотний). Якщо в склад складного ланцюга Маркова входять і замкнені множини станів, то, як вже відзначалося, їх можна окремо аналізувати як незвідний ланцюг Маркова. У зв’язку з цим важливим є розгляд марковських ланцюгів, які містять лише поглинаючі та незворотні стани.

Означення. Ланцюг Маркова називається поглинаючим (ланцюгом з поглинанням), якщо він складається лише з поглинаючих та незворотних станів.