Лекція № 7-8, 3 семестр, ІТП

Лекція № 7-8

Тема: Математичне сподівання дискретної випадкової величини і його властивості. Дисперсія дискретної випадкової величини, властивості. Середнє квадратичне відхилення

Питання лекції:

1. Математичне сподівання дискретної випадкової величини і його властивості.

2. Дисперсія дискретної випадкової величини, властивості.

3. Середнє квадратичне відхилення.

1*. Математичне сподівання дискретної випадкової величини і його властивості

Вичерпною характеристикою дискретної випадкової величини є її закон розподілу. Але він на практиці не завжди буває відомим. Іноді буває відомим тільки деяке середнє значення біля якого ґрунтуються можливі значення випадкової величини.

Нехай – величина, яка приймає значення – разів, – разів,…, – разів і , тоді середнє зважене цієї величини визначається за формулою

.

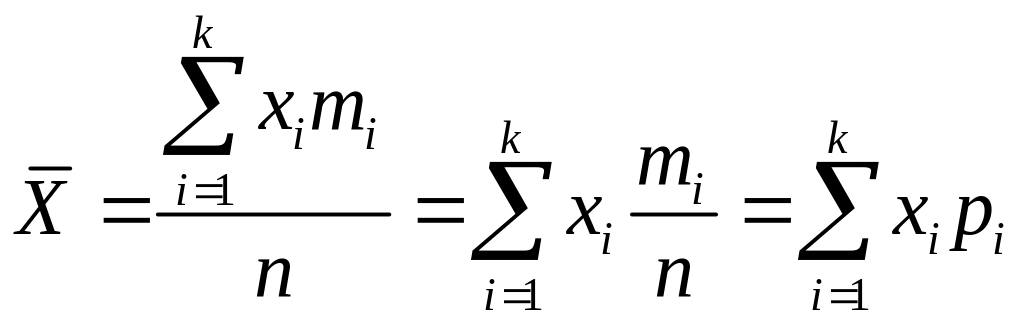Нехай тепер – дискретна випадкова величина, для якої закон розподілу задано таблицею

Середнє значення випадкової величини тепер буде середнім очікуваним значенням, яке називається математичним сподіванням. Математичне сподівання позначається так

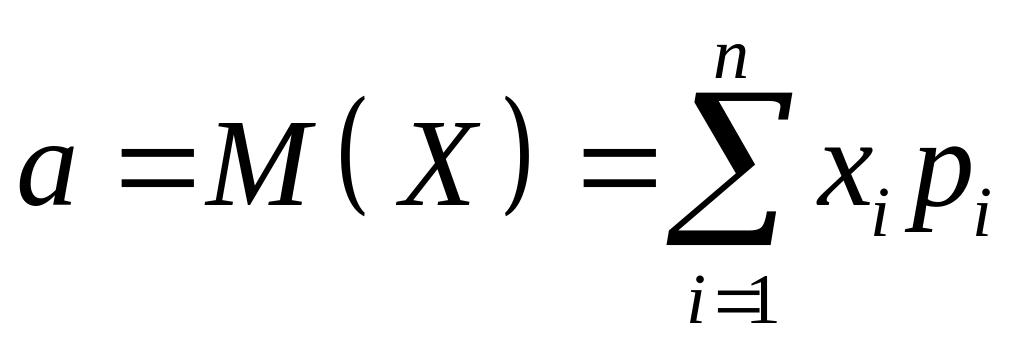. (1)

Отже, математичне сподівання випадкової дискретної величини дорівнює сумі добутків можливих значень випадкової величини і ймовірностей цих значень.

Таким чином, математичне сподівання є узагальненням середньої величини.

Математичне сподівання не є випадковою величиною. Якщо приймає скінчене число можливих значень, то .

Математичне сподівання числа появ події в однім іспиті дорівнює ймовірності цієї події.

Властивості математичного сподівання

1°. Математичне сподівання сталої величини дорівнює самій сталій величині:

.

Доведення. Будемо розглядати сталу як дискретну випадкову величину, яка має одне можливе значення і приймає його з ймовірністю . Отже,

.

2°. Математичне сподівання алгебраїчної суми скінченого числа випадкових величин дорівнює алгебраїчній сумі їх математичних сподівань

.

Доведення. Доведення проведемо для суми.

Нехай випадкові величини і задані наступними законами розподілу

Запишемо усі можливі значення . Для цього до кожного можливого значення добавимо кожне можливе значення , отримаємо , , , . Припустимо, що ці можливі значення різні і позначимо їх ймовірності відповідно через , , , .

Математичне сподівання величини дорівнює сумі добутків можливих значень на їх ймовірності:

або

(*)

Доведемо, що . Подія, яка складається з того, що прийме значення (ймовірність цієї події дорівнює ) тягне за собою подію, яка складається з того, що приймає значення або (ймовірність цієї події по теоремі додавання дорівнює ) і навпаки. Звідси і слідує, що . Аналогічно доводяться рівності

, і .

Підставляючи праві частини цих рівностей в співвідношення (*), отримаємо

або остаточно .

Аналогічно можна довести формулу для математичного сподівання різниці.

Наслідок. Математичне сподівання суми декількох випадкових величин дорівнює сумі математичних сподівань доданків

.

3°. Математичне сподівання добутку двох незалежних випадкових величин і дорівнює добутку їх математичних сподівань

.

Доведення. Нехай незалежні випадкові величини і задані своїми законами розподілу ймовірностей:

Упорядкуємо всі значення, які може приймати випадкова величина . Для цього перемножимо всі можливі значення на кожне можливе значення , отже отримаємо: , , і . Запишемо закон розподілу добутку

Математичне сподівання дорівнює сумі добутків усіх можливих значень на їх ймовірності

,

або

.

Отже, .

Наслідок. Математичне сподівання добутку декількох взаємно незалежних випадкових величин дорівнює добутку їх математичних сподівань

.

Наслідок. Сталий множник можна виносити за знак математичного сподівання

.

Доведення. .

4°. Математичне сподівання відхилення випадкової величини від її математичного сподівання дорівнює нулю

.

5°. Математичне сподівання числа появи події в незалежних іспитах дорівнює добутку числа іспитів на ймовірність появи події в кожному іспиті

.

6°. Математичне сподівання відносної частоти появи події в незалежних дослідах дорівнює ймовірності події

.

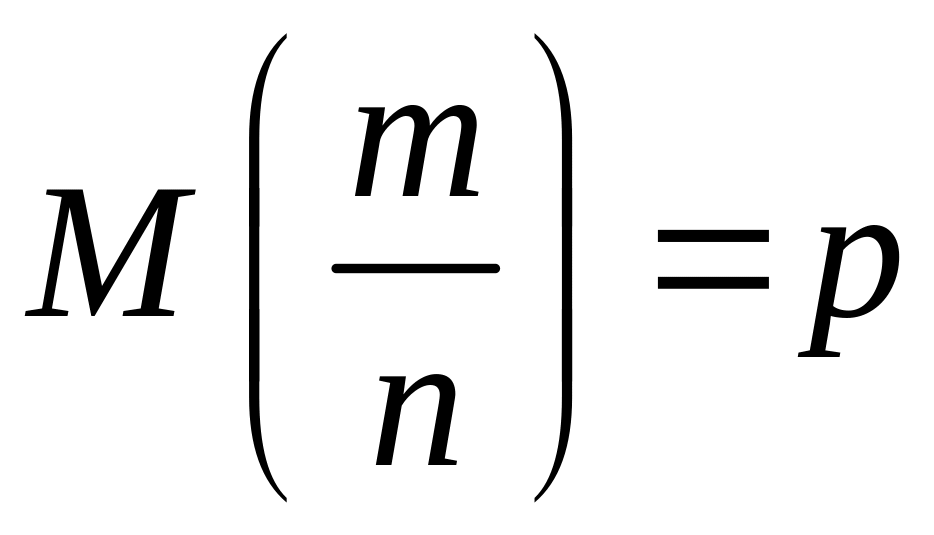Приклад 1. Стрілець стріляє по мішені. Число вибитих очок при одному пострілі є величина випадкова, яка характеризується наступним законом розподілу

Обчислити математичне сподівання числа вибитих очок.

Розв’язання. За формулою математичного сподівання маємо:

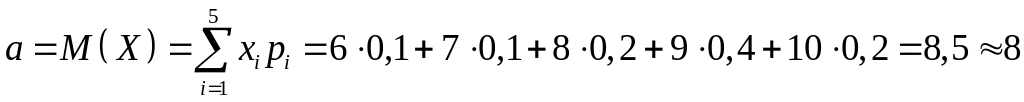очок.

Приклад 2. При складанні приладу для точної підгонки можуть бути потрібні , , , , спроб. Число спроб є випадкова величина , яка має наступний закон розподілу:

Скільки деталей повинен мати складальник, щоб скласти приладів?

Розв’язання. Обчислимо математичне сподівання числа спроб для складання одного приладу

деталі.

Для приладів: (деталей).