Условия равновесия между зарядами и электрическим полем.

При помещении металла ^[1] в электрическое поле   на свободные электроны действуют электрические силы, под действием которых электроны приходят в движение. 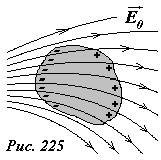Если электрическое поле не слишком велико, то электроны не могут покинуть объем металла и скапливаются на одной стороне проводника, с другой стороны проводника образуется недостаток электронов, поэтому положительный заряд ионов решетки оказывается нескомпенсированным (рис. 225). Таким образом, на поверхности проводника появляются электрические заряды, при этом суммарный заряд проводника остается, конечно, неизменным.

Напряженность поля всюду внутри проводника должна быть равна нулю Е=0. В соответствии с уравнением   это означает, что потенциал внутри проводника должен быть постоянным, т.е.   .

Явление возникновения электрических зарядов на проводнике под воздействием электрического поля называется электростатической индукцией, а возникшие заряды – индуцированными.

Появившиеся индуцированные заряды создают собственное индуцированное электрическое поле  , которое направлено в сторону, противоположную внешнему полю (рис. 226). Конечно, эти заряды создают поле как внутри проводника, так и вне его. Суммарное поле   отличается от внешнего поля.

Электри́ческая инду́кция (электри́ческое смеще́ние) — векторная величина, равная сумме вектора напряжённости электрического поля ивектора поляризации.

В СИ:  .

№16 Емкость. Емкость плоского конденсатора.

Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.

В системе СИ ёмкость измеряется в фарадах.

Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид

  где Q — заряд, U — потенциал проводника.

Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (еёдиэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара радиуса R равна (в системе СИ):

C = 4πε₀εR.

Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком —конденсатору. В этом случае взаимная ёмкость этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:

где S — площадь одной обкладки (подразумевается, что они равны), d — расстояние между обкладками, ε 

 относительная диэлектрическая проницаемость среды между обкладками, ε₀ = 8.854×10⁻¹² Ф/м — электрическая постоянная.

№17 Конденсаторы. Последовательное и параллельное соединение конденсаторов.

Конденсатор – это система из двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Так, например, две плоские металлические пластины, расположенные параллельно и разделенные слоем диэлектрика, образуют плоский конденсатор.

Если пластинам плоского конденсатора сообщить равные по модулю заряды противоположного знака, то напряженность электрического поля между пластинами будет в два раза больше, чем напряженность поля у одной пластины. Вне пластин напряженность электрического поля равна нулю, т. к. равные заряды разного знака на двух пластинах создают вне пластин электрические поля, напряженности которых равны по модулю, но противоположны по направлению.

Основной характеристикой конденсатора является его ёмкость, характеризующая способность конденсатора накапливать электрический заряд.

Также различают конденсаторы по форме обкладок: плоские, цилиндрические, сферические и другие.

Название	Ёмкость	Электрическое поле
Плоский конденсатор
Цилиндрический конденсатор
Сферический конденсатор
Сфера	C = 4πε0εrR1

Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею

  

Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади.

При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы, так как от источника питания они поступают только на внешние электроды, а на внутренних электродах они получаются только за счёт разделения зарядов, ранее нейтрализовавших друг друга. Общая ёмкость батареи последовательно соединённых конденсаторов равна

№18 Энергия уединенного проводника и заряженного конденсатора. Плотность энергии.

Если уединенный проводник имеет заряд q, то вокруг него существует электрическое поле, потенциал которого на поверхности проводника равен   , а емкость - С. Увеличим заряд на величину dq. При переносе заряда dq из бесконечности должна быть совершена работа равная   . Но потенциал электростатического поля данного проводника в бесконечности равен нулю   . Тогда

При переносе заряда dq с проводника в бесконечность такую же работу совершают силы электростатического поля. Следовательно, при увеличении заряда проводника на величину dq возрастает потенциальная энергия поля, т.е.

Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:

Применяя соотношение   , можно получить следующие выражения для потенциальной энергии W:

(16.2)

Для заряженного конденсатора разность потенциалов (напряжение) равна   поэтому соотношение для полной энергии его электростатического поля имеют вид

(16.3)

Плотность энергии — количество энергии на единицу объёма.

Плотность энергии электромагнитного поля может быть выражена через значения электрического и магнитного полей. В системе СИ:

№19 Электрический ток. Опыт Рикке. Носители тока. Определение тока как потока вектора плотности тока.

Электри́ческий ток — упорядоченное нескомпенсированное движение свободных электрически заряженных частиц, например, под воздействием электрического поля. Такими частицами могут являться: в проводниках — электроны, в электролитах — ионы (катионы и анионы), в газах - ионы и электроны, в вакууме при определенных условиях - электроны, в полупроводниках — электроны и дырки (электронно-дырочная проводимость).

Постоянный ток — ток, направление и величина которого слабо меняется во времени.

Переменный ток — это ток, направление и величина которого меняется во времени. 

Силой тока называется физическая величина, равная отношению количества заряда, прошедшего за некоторое время через поперечное сечение проводника, к величине этого промежутка времени.

Сила тока в системе СИ измеряется в Амперах.

По закону Ома сила тока I для участка цепи прямо пропорциональна приложенному напряжению U к участку цепи и обратно пропорциональна сопротивлению R проводникаэтого участка цепи :

Плотностью тока называется вектор, модуль которого равен отношению силы тока, протекающего через некоторую площадку, перпендикулярную направлению тока, к величине этой площадки, а направление вектора совпадает с направлением движения положительного заряда в токе.

Согласно закону Ома плотность тока в среде   пропорциональна напряжённости электрического поля   и проводимости среды  :

Плотность тока в системе СИ измеряется в амперах на квадратный метр.

В 1901 г. Рикке взял три цилиндра два медных и один алюминиевый с тщательно отшлифованными торцами. После взвешивания цилиндры были сложены вместе в последовательности медь - алюминий - медь. Через такой составной проводник непрерывно в течение года пропускался ток одного и того же направления. За все время через цилиндры прошел заряд, равный  . Взвешивание показало, что пропускание тока не оказало на массу цилиндров никакого влияния. При исследовании соприкасавшихся торцов под микроскопом не было обнаружено проникновение одного металла в другой.  Результаты опыта свидетельствовали о том, что перенос заряда в металлах осуществляется не атомами, а какими-то частицами, входящими в состав всех металлов. Чтобы отождествить носители тока в металлах с электронами, нужно было определить знак и числовое значение удельного заряда носителей.

№20 Понятие сторонних сил. ЭДС. Закон Ома для однородного участка цепи.

Для протекания тока в течение продолжительного времени на заряды в электрической цепи должны действовать силы, отличные по природе от сил электростатического поля, такие силы получили название сторонних сил. Эти силы могут быть обусловлены химическими процессами, диффузией носителей тока в неоднородной среде, электрическими (но не электростатическими) полями, порождаемыми переменными во времени магнитными полями, и т. д. Всякое устройство, в котором возникают сторонние силы, называется источником электрического тока. Сторонние силы характеризуют работой, которую они совершают над перемещаемыми по электрической цепи носителями заряда. Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС)  , действующей в электрической цепи или на ее участке. Представим стороннюю силу  , действующую на заряд q, в виде 

,

где векторная величина   представляет напряженность поля сторонних сил. Тогда на участке цепи ЭДС равна

.

Интеграл, вычисленный для замкнутой цепи, дает ЭДС, действующую в этой цепи,

.

Последнее выражение дает самое общее определение ЭДС и пригодно для любых случаев. Если известно, какие силы вызывают движение зарядов в данном источнике, то всегда можно найти напряженность поля сторонних сил и вычислить ЭДС источника. Физическая природа электродвижущих сил в разных источниках весьма различна. 

Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника: 

где R = const.

Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.

№21 Закон ома для участка цепи. Сопротивление. Дифференциальная форма записи закона Ома.

Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника: 

где R = const.

Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.

,

(7.6.3)

это запись закона Ома в дифференциальной форме.

Здесь   – удельная электропроводность.

Размерность σ – [ ].

№22 Последовательное и параллельное соединение сопротивлений.

Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же. 

Рис 1. Последовательное соединение сопротивлений

U = U1 + U2 + U3

где

U1 = IR1 U2 = IR2 и U3 = IR3

R = R1 + R2 + R3

I=const

№23 Разветвления цепи. Ветви, контуры, узлы. З-ны Кирхгофа

Эл.цепь называется линейной, если она содержит только линейные элементы.

Линейный элемент – это сопротивление, которое не зависит от протекающего тока и действующего напряжения.

Точка на схеме называется узлом, если в ней соединяются 2 или более проводов.

Ветвь эл.цепи – ее участок, состоящий из одного или нескольких элементов, соединенных так, что по ним

протекает один и тот же ток.

Контур эл.цепи – это замкнутый путь, проходящий по нескольким ветвям.

1 закон:

Сумма втекающих в узел токов равна сумме вытекающих из узла токов.

2 закон

Алгебраическая сумма ЭДС в контуре равна алгебраической сумме напряжений на всех элементах этого

контур

№24 Работа и мощность тока. Закон Джоуля-Ленца.

При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном учестке совершает работу 

ΔA = (φ1 – φ2) Δq = Δφ12 I Δt = U I Δt,

где U = Δφ₁₂ – напряжение. Эту работу называют работой электрического тока.

Если обе части формулы 

RI = U,

выражающей закон Ома для однородного участка цепи с сопротивлением R, умножить на IΔt, то получится соотношение 

R I2 Δt = U I Δt = ΔA.

Это соотношение выражает закон сохранения энергии для однородного участка цепи.

Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.

ΔQ = ΔA = R I2 Δt.

Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца.

Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена: 

Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).

Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцом^[1].

В словесной формулировке звучит следующим образом^[2]

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля

где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t₁ до t₂. В случае постоянных силы тока и сопротивления:

№25 Закон Био-савара-Лапласса для элементарной индукции

Закон Био-Савара-Лапласа: вектор индукции магнитного поля, созданного элементом проводника  , по которому течет ток  , имеет вид:

 

  ,                                      (1)

где  – радиус-вектор, проведенный от элемента   до той точки, в которой определяется индукция поля;   – магнитная постоянная.

·   

  В скалярной форме

№26 Индукция прямого тока. Индукция кругового тока в его центре. Индукция отрезка прямого тока.