Лабораторная работа №10 Определение оценок и доверительных границ для параметров логарифмически нормального распределения
Ц е л ь р а б о т ы:
найти оценки параметров
и
для
логарифмически нормального определения.
Н е о б х о д и м о е о б о р у д о в а н и е: микрокалькулятор; таблица исходных данных.
Основные теоретические сведения
Логарифмически нормальное распределение весьма часто встречается на практике. Оно возникает в задачах надежности технических систем (например, срок службы некоторых типов изделий, в экономических исследованиях и др.). Ему, как правило, подчиняются размеры частиц при дроблении, и поэтому оно встречается в геологии (процентное содержание минералов в природе) и др.
В данной работе уже известно, что распределение изучаемой случайной величины логарифмически нормально, и требуется оценить его параметры.
Следует иметь в виду, что, на не слишком больших отрезках функции логарифмически нормального распределения мало отличается от функции нормального распределения. Поэтому рекомендуется следующее правило: если распределение логарифмически нормально, но выборочный коэффициент вариации, т.е. отношение выборочной дисперсии к выборочному среднему, меньше 0,3, то можно считать, что исследуемая величина распределена нормально, и обрабатывать данные соответствующим образом.
Распределение положительной случайной величины Х называется логарифмически нормальным, если случайная величина
(91)
имеет нормальное распределение (см. ГОСТ 11.004-74).
Функция распределения величины Х имеет вид:
при Х>0
(92)
0
при Х
0
Таким образом, и являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Y, определенной по формуле (91).
Плотность распределения величины Х имеет вид
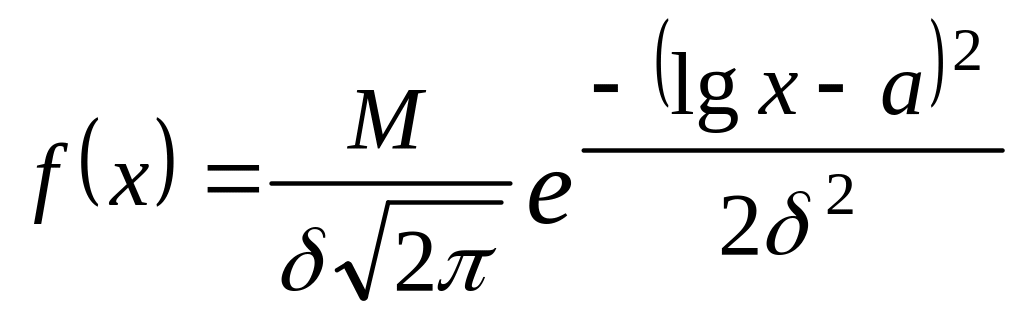при
X>0
(93)
0 при Х 0
где
.
Оценку параметра находят по формуле
(94)
где
-
совокупность наблюдений значений
случайной величины Х;
n-число
изделий, поставленных на испытание, или
число испытаний.
Если значения
параметра
неизвестно,
то оценка S2
параметра
,
(95)
где
определяют по формуле (94)
Оценка
параметра
(96)
где вычисляют по формуле (94).
Оценку можно использовать в тех случаях, когда не требуется большая точность вычислений. Поэтому надо найти также несмещенную оценку для :
,
(97)
где Мк определяют по табл. 25 при K=n-1.
Таблица 25
Значения коэффициентов МK.
-
К
МK
K
МK
К
МK
1
1,253
10
1,025
19
1,013
2
1,128
11
1,023
20
1,013
3
1,085
12
1,021
25
1,010
4
1,064
13
1,019
30
1,008
5
1,051
14
1,018
35
1,007
6
1,042
15
1,017
40
1,006
7
1,036
16
1,016
45
1,006
8
1,032
17
1,015
50
1,005
9
1,028
18
1,014
60
1,004
Определение доверительных границ для параметра а
Нижнюю и верхнюю доверительные границы (соответственно ан и аВ для параметра а при известном значении параметра σ находят по следующим формулам:
(98)
(99)
где
- вычисляют по формуле (94), а uγ
- по таблицам.
Доверительные границы для параметра a при неизвестном значении σ находят по формулам:
(100)
(101)
где и S определяют соответственно по формулам (94) и (97), а tγ - в табл. 26 по заданным значениям n - 1 и γ.
Таблица 26
Значения коэффициентов tγ
-
n -1
Значения коэффициентов tγ при односторонней доверительной
вероятности γ
0,80
0,90
10,95
0,975
0,990
0,995
0,9975
0,9990
1
1,375
3,078
6,314
12,71
31,82
63,66
127,3
318,3
2
1,061
1,886
2,920
4,303
6,965
9,925
14,09
22,33
3
0,978
1,638
2,353
3,182
4,541
5,841
7,453
10,21
4
0,941
1,533
2,132
2,776
3,747
4,604
5,598
7,173
5
0,920
1,476
2,015
2,571
3,365
4,032
4,773
5,893
6
0,906
1,440
1,943
4,447
3,143
3,707
4,317
5,208
7
0,896
1,415
1,895
2,365
2,998
3,449
4,029
4,785
8
0,889
1,397
1,859
2,306
2,896
3,335
3,832
4,501
9
0,883
1,383
1,833
2,252
2,821
3,250
3,690
4,297
10
0,879
1,372
1,812
2,228
2,764
3,169
3,581
4,144
11
0,876
1,363
1,796
2,201
2,713
3,106
3,497
4,025
12
0,873
1,356
1,782
2,170
2,680
3,054
3,497
3,930
13
0,870
1,350
1,771
2,160
2,650
3,012
3,373
3,852
14
0,868
1,345
1,761
2,145
2,624
2,977
3,326
3,787
15
0,866
1,341
1,753
2,131
2,602
2,947
3,286
3,286
16
0,865
1,337
1,746
2,120
2,583
2,921
3,252
3,686
17
0,863
1,333
1,740
2,110
2,567
2,898
3,222
3,646
18
0,862
1,330
1,734
2,101
2,552
2,878
3,197
3,611
19
0,861
1,328
1,729
2,093
2,539
2,861
3,174
3,579
20
0,860
1,325
1,725
2,086
2,528
2,845
3,153
3,552
21
0,859
1,323
1,721
2,080
2,518
2,831
3,135
3,527
22
0,858
1,321
1,717
2,074
2,508
2,819
3,119
3,505
23
0,858
1,319
1,714
2,069
2,500
2,807
3,104
3,485
24
0,857
1,318
1,711
2,064
2,492
2,797
3,090
3,467
25
0,856
1,316
1,708
2,060
2,485
2,787
3,078
3,450
26
0,856
1,315
1,706
2,056
2,479
2,779
3,067
3,435
27
0,855
1,314
1,703
2,052
2,473
2,771
3,056
3,421
28
0,855
1,313
1,701
2,048
2,467
2,763
3,047
3,408
29
0,854
1,311
1,699
2,045
2,462
2,756
3,038
3,396
30
0,854
1,310
1,697
2,042
2,457
2,750
3,030
3,385
32
0,853
1,309
1,694
2,037
2,449
2,737
3,015
3,365
34
0,853
1,307
1,691
2,032
2,441
2,728
3,002
3,348
36
0,852
1,305
1,688
2,028
2,434
2,719
2,990
3,333
38
0,852
1,304
1,686
2,024
2,429
2,712
2,980
3,319
40
0,851
1,303
1,684
2,021
2,423
2,704
2,971
3,307
Определение доверительных границ для параметра σ
Нижнюю и верхнюю доверительные границы для параметра σ (соответственно σН и σВ) определяют по следующим формулам:
(102)
(103)
где S находят по формуле (97), ZН и ZВ – соответственно по табл. 27 и 28 при К=n-1, если значения параметра а неизвестны.
Таблица 27
Значения коэффициентов ZН
-
К
Значения коэффициентов ZН при односторонней доверительной
вероятности γ
0,80
0,90
0,95
0,975
0,990
0,995
0,9975
0,9990
2
0,788
0,788
0,578
0,521
0,466
0,434
0,408
0,380
3
0,804
0,804
0,620
0,566
0,514
0,483
0,457
0,429
4
0,817
0,817
0,649
0,599
0,549
0,519
0,493
0,455
5
0,828
0,828
0,672
0,624
0,576
0,546
0,521
0,494
6
0,837
0,837
0,690
0,644
0,597
0,569
0,544
0,517
7
0,845
0,845
0,705
0,661
0,616
0,588
0,563
0,536
8
0,852
0,852
0,718
0,675
0,631
0,604
0,580
0,553
9
0,859
0,788
0,729
0,688
0,645
0,618
0,549
0,568
10
0,864
0,804
0,699
0,739
0,656
0,630
0,607
0,581
11
0,869
0,817
0,748
0,708
0,667
0,641
0,619
0,593
12
0,872
0,828
0,755
0,717
0,677
0,651
0,629
0,604
13
0,874
0,837
0,762
0,725
0,685
0,660
0,638
0,614
14
0,877
0,845
0,769
0,732
0,693
0,669
0,647
0,623
15
0,881
0,852
0,775
0,739
0,700
0,676
0,655
0,631
16
0,884
0,859
0,780
0,745
0,707
0,683
0,662
0,638
17
0,886
0,864
0,785
0,713
0,690
0,690
0,669
0,646
18
0,888
0,869
0,790
0,756
0,719
0,696
0,675
0,652
19
0,836
0,872
0,760
0,725
0,725
0,702
0,681
0,658
20
0,894
0,874
0,798
0,765
0,730
0,687
0,707
0,664
22
0,898
0,877
0,773
0,739
0,739
0,717
0,697
0,675
24
0,901
0,881
0,812
0,781
0,747
0,726
0,707
0,685
26
0,904
0,884
0,818
0,788
0,755
0,734
0,715
0,694
28
0,907
0,886
0,823
0,794
0,762
0,741
0,723
0,702
30
0,909
0,888
0,828
0,799
0,768
0,748
0,730
0,709
35
0,915
0,836
0,838
0,811
0,781
0,762
0,745
0,725
40
0,919
0,894
0,847
0,821
0,792
0,774
0,757
0,738
45
0,923
0,898
0,854
0,829
0,802
0,784
0,768
0,750
50
0,927
0,901
0,861
0,837
0,810
0,793
0,777
0,760
60
0,932
0,904
0,871
0,349
0,824
0,808
0,793
0,776
70
0,937
0,907
0,879
0,858
0,835
0,820
0,805
0,789
80
0,941
0,909
0,88§
0,866
0,844
0,829
0,815
0,801
90
0,943
0,915
0,892
0,373
0,852
0,338
0,825
0,810
100
0,946
0,919
0,897
0,879
0,858
0,845
0,832
0,818
Таблица 28
Значения коэффициентов ZВ
-
К
Значения коэффициентов ZВ при односторонней доверительной
вероятности γ
0,80
0,90
0,95
0,975
0,990
0,995
0,9975
0,9990
2
2,12
3,08
4,42
6,28
9,97
14,1
19,89
31,6
3
1,73
2,27
2,92
3,73
5,11
6,47
8,19
11,1
4
1,56
1,94
2,37
2,87
3,67
4,40
5,29
6,64
5
1,46
1,76
2,09
2,45
3,00
3,48
4,04
4,88
6
1,40
1,65
1,92
2,20
2,62
2,98
3,38
2,97
7
1,35
1,57
1,80
2,04
2,38
2,66
2,97
3,42
8
1,32
1,51
1,71
1,92
2,20
2,44
2,69
3,06
9
1,29
1,47
1,65
1,83
2,08
2,28
2,49
2,79
10
1,27
1,43
1,59
1,75
1,98
2,15
2,34
2,60
11
1,25
1,40
1,55
1,70
1,90
2,06
2,22
2,45
12
1,24
1,38
1,52
1,65
1,83
1,98
2,13
2,33
13
1,23
1,36
1,49
1,61
1,78
1,91
2,05
2,23
14
1,22
1,34
1,46
1,58
1,73
1,85
1,98
2,15
15
1,21
1,32
1,44
1,55
1,69
1,81
1,93
2,08
16
1,20
1,31
1,42
1,52
1,66
1,76
1,87
2,01
17
1,19
1,30
1,40
1,50
1,63
1,73
1,83
1,96
18
1,18
1,28
1,38
1,48
1,60
1,70
1,79
1,92
19
1,18
1,27
1,37
1,46
1,58
1,67
1,75
1,87
20
1,17
1,26
1,36
1,44
1,56
1,64
1,72
1,84
22
1,16
1,25
1,34
1,42
1,52
1,60
1,67
1,77
24
1,15
1,24
1,32
1,39
1,49
1,56
1,63
1,72
26
1,15
1,23
1,30
1,37
1,46
1,53
1,59
1,72
28
1,14
1,22
1,29
1,35
1,44
1,50
1,56
1,64
30
1,13
1,21
1,27
1,34
1,42
1,48
1,53
1,61
35
1,12
1,19
1,25
1,30
1,38
1,43
1,47
1,54
40
1,11
1,17
1,23
1,28
1,34
1,39
1,43
1,49
45
1,10
1,16
1,21
1,26
1,32
1,36
1,40
1,46
50
1,10
1,15
1,20
1,24
1,30
1,34
1,37
1,42
60
1,09
1,14
1,18
1,22
1,27
1,30
1,33
1,37
70
1,08
1,13
1,16
1,20
1,24
1,27
1,30
1,34
80
1,08
1,12
1,15
1,18
1,22
1,25
1,27
1,31
90
1,07
1,11
1,14
1,17
1,21
1,23
1,25
1,29
100
1,07
1,10
1,13
1,16
1,19
1,22
1,24
1,27
Доверительный интервал (бесконечный в одностороннем случае и конечный в двустороннем) накрывает значение параметра с вероятностью γ в одностороннем случае и γ* в двустороннем.