
- •Введение
- •Лабораторная работа № 1
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 4 Графо-аналитический метод определения параметров закона распределения показателей надежности
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 5 Определение оптимального ресурса и периодичности обслуживания узлов трения при простом процессе восстановления
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 6 Оценка эффективности использования ресурса деталей при групповых заменах
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 7 Прогнозирование расхода запасных частей при групповых заменах
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Лабораторная работа № 8 Обработка эмпирических данных, принадлежащих экспоненциальному закону распределения
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 9 Методы прогнозирования надежности
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №10 Определение оценок и доверительных границ для параметров логарифмически нормального распределения
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №12 Методика расчета проектной надежности технической системы
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 13 Применение критерия Колмогорова
- •Основные теоретические сведения
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Список литературы
- •Содержание
Лабораторная работа № 9 Методы прогнозирования надежности
Ц е л ь р а б о т ы: рассчитать ресурс технической системы до первого капитального ремонта за период 2006…2009 гг.
Н е о б х о д и м о е о б о р у д о в а н и е: микрокалькулятор; таблица исходных данных.
Основные теоретические сведения
Современные методы прогнозирования надежности могут быть разделены на три основные группы:
1) методы экспертных оценок;
2) методы моделирования, включающие физические, физико-математические и информационные модели;
3) статистические методы прогнозирования, основные на интерполяции или экстраполяции данных, полученных в результате предварительных исследований.
В зависимости от длительности прогнозируемого периода различают прогнозы: краткосрочные (до 5лет), среднесрочные (5…15 лет), долгосрочные (свыше 15 лет). Глубину ретроспективного анализа информации об объекте определяют длительностью периода: чем больше
прогнозируемый период, тем больший срок берут для анализа закономерности изменения надежности объекта в прошлом. Считается, что ретроспективный период должен превышать прогнозируемый период примерно в 2 …3 раза.
Установлено, что для большинства задач прогнозирования надежности технических систем достаточно получить решение с точностью 10 … 15%. Информация об изменении состояния элементов систем обычно невелика. Сбор информации в полном объеме связан с большими материальными затратами, техническими трудностями, требует много времени. Это ограничивает объем исходной информации. Эти причины предопределяют использование достаточно простых методов прогнозирования, которые позволяют получить решение задачи в минимальные сроки и с использованием простого математического аппарата.
Методы прогнозирования выбирают с учетом: а) задач прогнозирования; б) количества и качества исходной информации; в) характера реального процесса изменения показателя надежности прогнозируемого параметра, (рис. 2).
Обработка и анализ исходной информации позволяют построить математическую модель объекта прогнозирования. Точность модели определяется: 1) целью и задачами прогнозирования; 2) количеством и качеством информации.

Рис. 2. Схема прогнозирования надежности
Сущность методов прогнозирования, основанных на экспертных оценках, заключается в обобщении, статистической обработке и анализе мнений специалистов относительно перспектив развития данной области.
Методы моделирования базируются на основных положениях теории подобия. Процедура прогнозирования с использованием моделирования заключена в следующем. На основании показателей подобия модификации А технической системы, уровень надежности которой исследован ранее, и некоторых свойств модификации Б той же системы, уровень надежности которой необходимо оценить, прогнозируют показатели надежности Б на некоторый период времени.
Метод моделирования состоит из трех этапов:
1) формирование модели исследования;
2) проведение экспериментальных исследований;
3) пересчета полученных значений с модели на натуральный объект.
В основу прогнозирования надежности технических систем и их элементов могут быть положены физические и математические методы моделирования. Задача заключена в определении условий, при которых модель приобретает прогностическую функцию допущений и ограничений, накладываемых на область применения модели и период прогнозирования.
Один из статистических методов прогнозирования – метод экстраполяции. В основе прогнозирования надежности методом экстраполяции лежат закономерности изменения прогнозируемых параметров во времени.
Если известно
значение функции в точках
![]() ,
лежащих внутри интервала
,
лежащих внутри интервала
![]() ,
то процедуру установления значения
функции
,
то процедуру установления значения
функции
![]() в точках Х, лежащих вне интервала
,
называют экстраполяцией.
в точках Х, лежащих вне интервала
,
называют экстраполяцией.
Прогнозирование состоит из нескольких этапов:
1) анализа исходных данных и построения графика, иллюстрирующего изменение прогнозируемого параметра во времени;
2) определение аналитического выражения (математической модели), описывающего закономерность изменения прогнозируемого параметра;
3) экстраполяции полученного уравнения и прогнозирования показателей надежности за данный период.
После построения графиков, отражающих связь между переменными, подбирают аналитическую функцию. Подбор функции составляет важную часть прогнозирования. Выбор кривой определяется субъективными факторами, и здесь большое значение имеет правильное логическое объяснение зависимости анализируемых параметров с учетом опыта их развития в прошлом. По возможности нужно стремиться подбирать простые аналитические функции с минимальным числом переменных.
Существует ряд методов определения параметров эмпирических формул: метод выбранных точек; метод средних; метод наименьших квадратов.
Рассмотрим метод
выбранных точек. Пусть в результате
наблюдений получена система опытных
данных:
![]()
![]() при
при
![]() =1,
2,…,n.
Необходимо определить параметры функции
=1,
2,…,n.
Необходимо определить параметры функции
![]() .
.
На координатную
плоскость XOY
наносят точки и проводят плавную кривую,
по возможности примыкающую к точкам
.
На кривой выбирают систему m
(по числу параметров) точек с координатами
xi
и
![]() при
при
![]() =
1,2,…,m.
Выбранные точки должны быть равномерно
распределены по всей кривой. Для удобства
обычно берут абсциссы этих точек,
совпадающие с крупными делениями оси
OX
координатной сетки. Далее измеряют
ординаты выбранных точек
yi.
Параметры
=
1,2,…,m.
Выбранные точки должны быть равномерно
распределены по всей кривой. Для удобства
обычно берут абсциссы этих точек,
совпадающие с крупными делениями оси
OX
координатной сетки. Далее измеряют
ординаты выбранных точек
yi.
Параметры
![]() в общем случае определяют из системы m
уравнений при
=
1,2,…,m:
в общем случае определяют из системы m
уравнений при
=
1,2,…,m:
![]()
Для определения
параметров линейной зависимости решают
систему уравнений:
![]() ,
,
![]() .
.
Для случая
квадратичной зависимости
![]() коэффициенты
,
b
и c
определяют из системы трех уравнений:
коэффициенты
,
b
и c
определяют из системы трех уравнений:
![]() ,
,
![]() ,
,
![]() .
.
Метод выбранных точек является весьма простым и наглядным, но обладает малой точностью.
При прогнозировании надежности технических систем и их элементов наиболее часто используют такие зависимости, как линейная и квадратичная функции.
Общий вид линейной функции выражен формулой:
![]() (88)
(88)
где
![]() и
и
![]() - постоянные коэффициенты.
- постоянные коэффициенты.
Коэффициент
![]() :
:
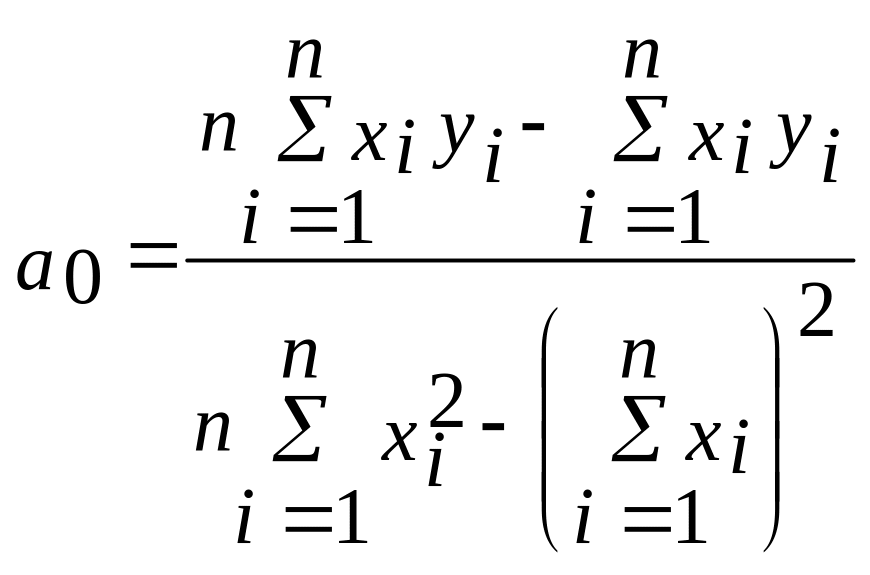 .
(89)
.
(89)
Коэффициент
![]() определяет угол наклона прямой к оси
абсцисс. Для нахождения значения
используют выражение или находят по
формуле
определяет угол наклона прямой к оси
абсцисс. Для нахождения значения
используют выражение или находят по
формуле
![]()
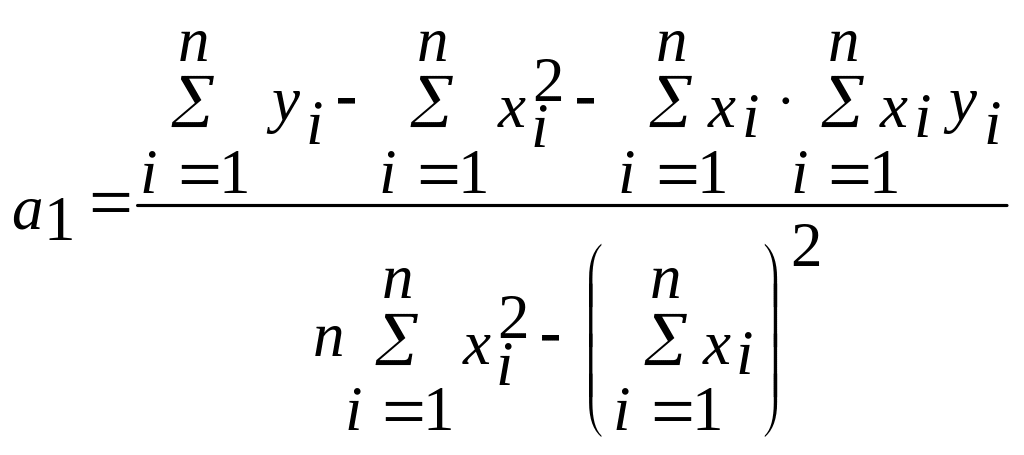 .
(90)
.
(90)
