6. Многогранники. Пересечение многогранника плоскостью

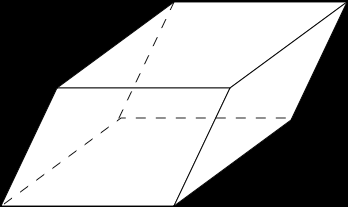
Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Вершины и стороны многогранников являются вершинами и ребрами многогранников. Они образуют пространственную сетку. Если вершины и ребра многогранника находятся по одну сторону плоскости любой из его граней, то многогранник называют выпуклым, все его грани – выпуклые.

М ногогранник называется метрически правильным, если все его грани являются правильными многоугольниками. К ним относятся куб, тетраэдр, октаэдр, икосаэдр, додекаэдр.

Пересечение многогранника плоскостью

 Геометрическая фигура, получающаяся в результате пересечения многогранника плоскостью, называется сечением многогранника.  Сечение представляет собой плоский многоугольник с внутренней областью. В частном случае эти многоугольники могут распадаться на несколько многогранников, вырождаться в прямые и точки.  Сечение многогранника плоскостью можно построить двумя способами: 1. По точкам пересечения с плоскостью ребер многогранника.  2. По линиям пересечения граней многогранника с плоскостью.  В первом случае задача сводится к определению точек пересечения прямой с плоскостью. Во втором случае - к определению линий пересечения плоскостей.  В ряде случаев целесообразно комбинированное применение обоих способов.

7.Приобразование чертежа. Натуральная величина отрезка

Решение многих задач упрощается, если прямые, плоские фигуры и другие элементы геометрических тел находятся в частном положении, которое может быть обеспечено преобразованием чертежа.  Преобразование чертежа может быть выполнено способом вращения, способом проецирования на дополнительную плоскость, способом плоскопараллельного переноса и другими. Наиболее часто применяются способ вращения и способ проецирования на дополнительную плоскость.

СПОСОБ ВРАЩЕНИЯ: Способ вращения геометрической фигуры вокруг некоторой оси состоит в том, что фигура вращается вокруг оси до требуемого положения относительно заданной неподвижной системы плоскостей проекций.

СПОСОБ ПРОЕЦИРОВАНИЯ НА ДОПОЛНИТЕЛЬНУЮ ПЛОСКОСТЬ

   Этот способ широко применяют в практике выполнения чертежей. Сущность способа проецирования на дополнительную плоскость проекций заключается в следующем: положение точек, линий, плоских фигур, геометрических тел в пространстве не изменяется, а данная система плоскостей проекций дополняется плоскостями, расположенными к П₁ или П₂, или друг к другу под прямым углом.

Натуральная величина

При нахождении решения задачи иногда бывает необходимость в определении натуральной величины отрезка.

Можно решить так: способ прямоугольного треугольника, способ вращения, способ плоскопараллельного перемещения, способ заменой плоскостей проекций.

8.Криволинейная поверхности способы задания.

Различны и способы задания кривой линии:

аналитический – кривая задана математическим уравне-

нием;

графический – кривая задана визуально на носителе графической информации;

табличный – кривая задана координатами последовательного ряда точек. В основу классификации кривых положена природа их

уравнений. Уравнением кривой линии называется такое соотношение

между переменными, которому удовлетворяют координаты

точки, принадлежащей кривой. Кривые подразделяются на алгебраические и трансцен-дентные в зависимости от того является ли их уравнение алгебраическим или транцендентным в прямоугольной системе координат. Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими, остальные пространственными..

Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой). Например, если прямая пересекает ось вращения, то при её вращении получится коническая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — однополостный гиперболоид вращения. Одна и та же поверхность может быть получена вращением самых разнообразных кривых.

9. Точка и линия на поверхности В общем случае линия может принадлежать поверхности или не принадлежать. Линия принадлежит поверхности, если все ее точки принадлежат этой поверхности. Исключение составляет случай, когда линия представлена прямой, а поверхность — плоскостью. В этом случае для принадлежности прямой плоскости достаточно, чтобы хотя бы две точки ее принадлежали этой поверхности

Задача определения принадлежности точки поверхности решается следующим способом. Если заданы проекции элементов поверхности и точки, необходимо на одной из плоскостей проекций через заданную точку провести линию, принадлежащую поверхности, и построить проекцию этой линии на одной плоскости проекций. Если вторая проекция пройдет через вторую проекцию точки — точка принадлежит поверхности, если не пройдет — не принадлежит

10.Общий метод построения линии пересечения поверхностейОбщим способом построения линии пересечения одной поверхности другою является нахождение точек этой линии при помощи некоторых секущих поверхностей.

На рисунке покажем что поверхности 1 и 2 пересечены некоторой поверхностью 3; эта вспомогательная поверхность пересекает поверхность 1 по линии АВ и CD.Точка K, в которой пересекаются линии АВ и CD, общая для поверхностей 1 и 2 следовательно, принадлежит линии их пересечения. Повторяя такой прием, получаем ряд точек искомой линии

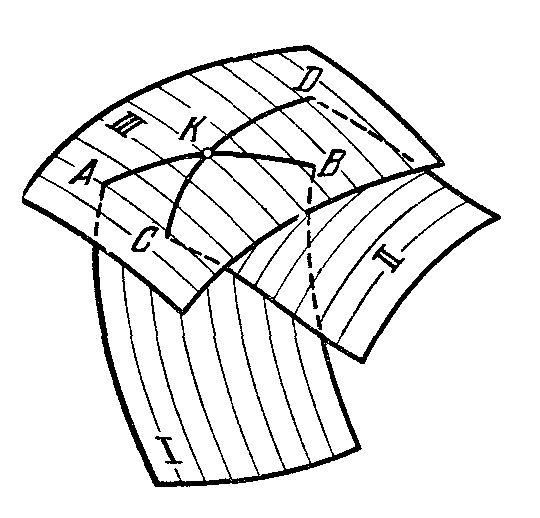
Применяя указанный общий способ для построения линии пересечения двух кривых поверхностей мы можем:

1)Пересекать поверхности вспомогательными плоскостями

2)Пересекать поверхности вспомогательными кривыми поверхностями(например сферами)