Завдання 3. Визначення моменту інерції маятника j0 .

Момент інерції маятника складається з моменту інерції хрестовини та моменту інерції рухливих вантажців на спицях

J=J₀+J_гр. (11)

Якщо вантажці можна вважати точковими масами, то J_гр=4mR², і, підставляючи цей вираз у (11), одержимо

J=J₀+4mR². (12)

Скориставшись методом найменших квадратів (програма № 4), розрахувати значення моменту інерції хрестовини без вантажів.

Контрольні питання

1. Запишіть визначення векторів повороту d, кутової швидкості , кутового прискорення .

5. Дайте визначення моментів сили та імпульсу. Намалюйте вказані вектори.

6. Доведіть вираз для моменту імпульсу .

7. Дайте визначення моменту інерції J точкового тіла та макроскопічного тіла. Наведіть приклади виразів моменту інерції J для найпростіших тіл. Запишіть теорему Штейнера.

8. Виведіть рівняння обертового руху Ньютона .

9. Виведіть вирази (8,10).

10. Поясніть спосіб розрахунку границі довірчого інтервалу виміру та у чому його сутність.

Лабораторна робота № 4

Визначення моменту інерції тіла методом крутильних коливань

Мета роботи

• обчислити момент інерції тіла невідомої геометрії

Прилади та обладнання

• секундомір,

• крутильний маятник,

• тіло невідомої геометрії.

Коротка теорія.

Одним із методів експериментального визначення моменту інерції тіла є метод Гауса, заснований на використанні обертальних чи крутильних коливань.

Рух крутильного маятника докладно розглянуто в Додатку (§ 15). Нижче буде розглянуте застосування крутильного маятника для визначення моменту інерції тіла невідомої геометрії.

Період вільних гармонічних крутильних коливань тіла з моментом інерції J визначається по формулі

,

де f  модуль крутіння дроту (стрижня). Період вільного гармонічного коливання тим більше, чим більше інертність тіла і чим менш пружна пружина чи дріт, на якій воно підвішене.

Виміривши період Т крутильних коливань, можна визначити момент інерції тіла, що робить ці коливання. Однак для цього необхідно знати модуль крутіння f.

Метод Гауса полягає в застосуванні крутильних коливань і виключенні невідомого модуля крутіння f при уведенні ще одного тіла геометрично правильної форми. Період коливань вимірюють двічі

а) для досліджуваного тіла (диск), для якого період коливань маятника

,

б) для складного тіла, складеного з досліджуваного тіла з моментом інерції J_х і тіла правильної форми (у нашому випадку вид циліндричного кільця) із моментом інерції J. Для цього складного тіла період коливань визначається по формулі

.

Звівши обидві частини виражень для періодів у квадрат і, поділяючи одне на друге, одержимо пропорцію

з якої випливає

.

.

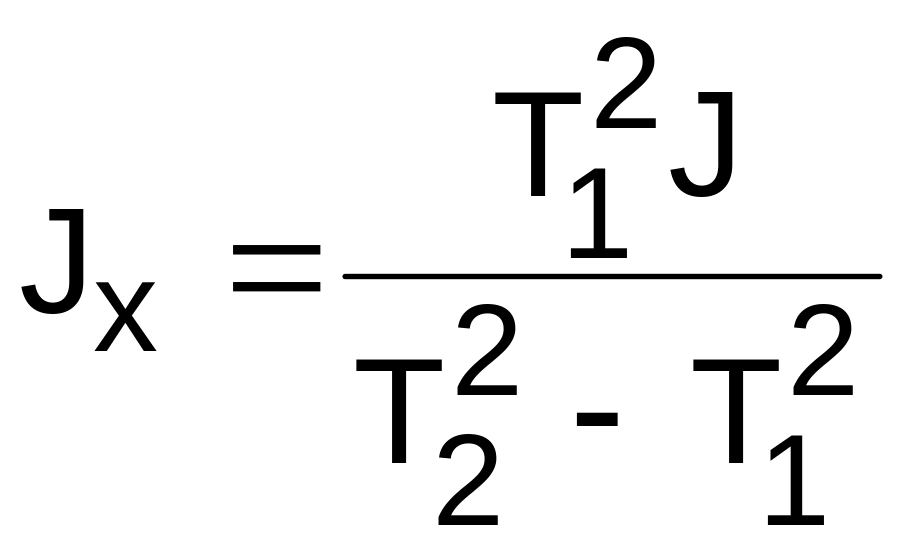Момент інерції J тіла правильної форми (циліндричного кільця) визначають за формулою

,

де R і r - відповідно зовнішній і внутрішній радіуси кільця, а d₁ і d₂ їхні діаметри, m  маса кільця.

Зовнішній і внутрішній діаметри тіла вимірюють штангенциркулем, а масу знаходять зважуванням на вагах. Періоди коливань Т₁ і Т₂ досліджуваного й складного тіла визначають, вимірюючи час 20 коливань секундоміром ( t₁ і t₂).

Момент інерції обчислюють по робочій формулі

.