§ 25. Теорема Больцмана про рівнорозподіл енергії

Теорема Больцмана про рівнорозподіл енергії за ступенями свободи установлює, що на кожну поступальну або обертову ступінь свободи приходиться енергія , а на коливальну ступінь  kT (коливальна ступінь характеризується наявністю кінетичної  та потенціальної  енергій).

Ступені свободи (вільності) тіла  незалежні параметри, які визначають положення тіла в просторі. Розрізняють поступальні, обертові та коливальні ступені свободи, зокрема, точкове тіло в просторі має три поступальні ступені свободи, наприклад, три декартові координати x,y,z. Зв'язки - рівняння, які описують обмеження руху тіла іншими тілами. Наявність зв'язків зменшує число ступенів свободи на їх кількість. Система з N частинок може бути визначена в просторі положенням центра мас X_C,Y_C,Z_C  3 поступальні ступені свободи, поворотами системи відносно осей X,Y,Z  3 обертові ступені (2 для лінійної системи частинок), та відповідно  3N - 6(5) коливальними ступенями свободи.

Внутрішня теплова енергія молекули з N атомами визначається як

,

де

де n_пост - число поступальних, n_оберт  число обертових і n_кол  число коливальних ступенів свободи. Зауважимо, що n_пост + n_оберт + n_кол = 3N. Для звичайних температур теплової енергії kТ недостатньо для теплових збуджень коливань у молекулі і тому покладається, що зв'язки частинок у молекулі жорсткі і n_кол = 0.

Якщо газ має масу m і молярну масу , то він маєь частинок, а його внутрішня енергія теплового руху дорівнює

=,

або

U = .

Якщо врахувати, що стан ідеального газу визначається рівнянням Клапейрона-Менделєєва

,

то вираз для внутрішньої енергії прийме вид

.

§ 26. Робота термодинамічної системи

Умовою здійснення термодинамічною системою елементарної роботи А є переміщення взаємодіючих із нею зовнішніх тіл. При цьому елементарна робота А' зовнішніх тіл над системою А' = - А.

Р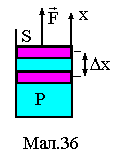 оботою розширення газу називається робота, що здійснюється системою проти сил зовнішнього тиску. При цьому елементарна робота дорівнює

А = PdV і .

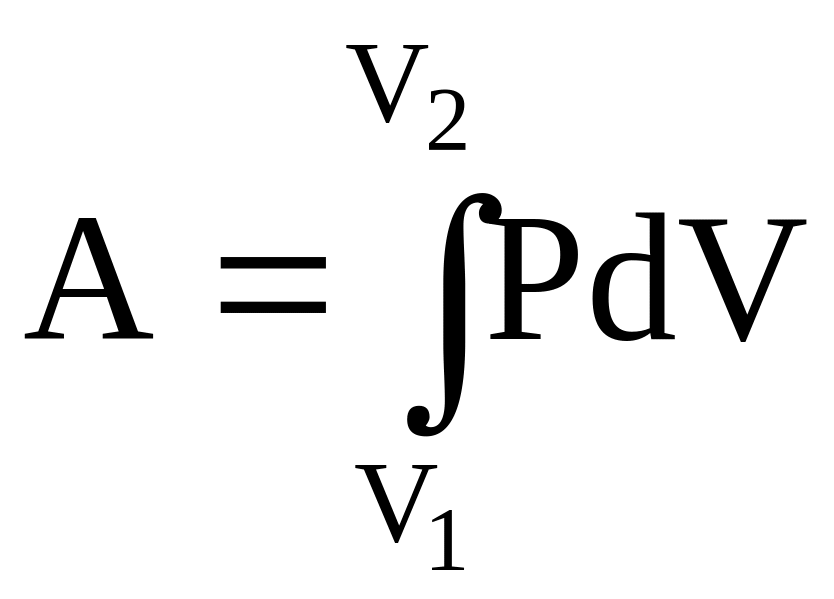Наприклад, при розширенні газу в циліндрі (див. Мал. 36), газ створює тиск Р на поршень площею S і в результаті на нього діє сила F = PS. При переміщенні поршня на dx, газ виконує роботу

,

де dV - приріст об'єму газу.

Робота розширення газу від об'єму V₁ до об'єму V₂ при ізотермічному процесі ( ) дорівнює A= . З рівняння Клапейрона - Менделєєва маємо

,

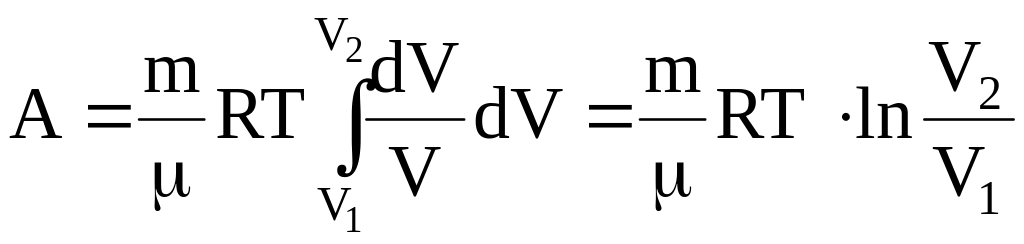
Робота розширення газу від V₁ до V₂ при ізобаричному процесі ( )

.

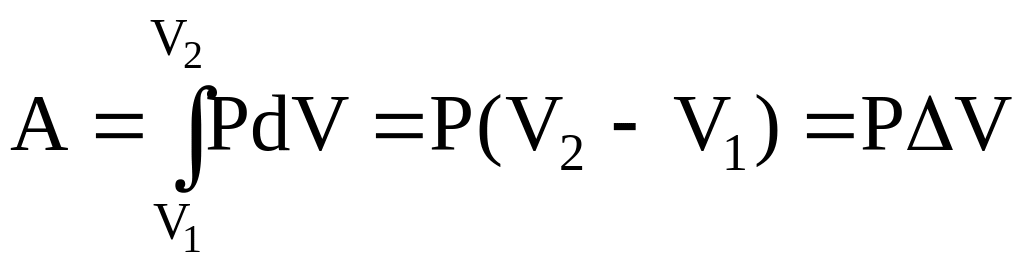§ 27. Перший закон (начало) термодинаміки

Перший закон (начало) термодинаміки  передане системі тепло , створює приріст внутрішньої енергії системи dU та йде на виконання нею елементарної роботи

(нагадаємо, що символом позначаються елементарні величини, які не є функціями стану системи).

Перший закон термодинаміки виражає загальний закон збереження та перетворення енергії і не визначає напрямок протікання процесу теплопередачі, а також умов, за яких відбувається теплопередача. Це питання врегульовується другим законом термодинаміки.

§ 28. Адіабатичний процес

Адіабатичним називається термодинамічний процес, що переводить термодинамічну систему в різні рівноважні стани без теплообміну із зовнішнім середовищем, тобто коли Q=0. Для ідеального газу справджується рівняння адіабати

, (1)

де  =  стала адіабати, що залежить від структури складових газу. Разом із тим рівноважні стани описуються одночасно і рівнянням Клапейрона - Менделєєва .

Щоб одержати рівняння (1), запишемо перший закон термодинаміки у вигляді

. (2)

Узявши диференціал по P,V,T у рівнянні стану , матимемо

, (3)

і після підстановки в перший закон термодинаміки одержимо

. (4)

Поділивши ліву частину (4) на PV, одержимо

,

що й треба було довести.

Користуючись об'єднаним газовим законом , одержане рівняння адіабати можна записати в таких видах

, . (5)

Робота розширення газу від до при адіабатичному процесі може бути одержана з першого начала Q=dU+A=0

A=-dU. (6)

В інших виразах роботу можна знайти прямим обчисленням

. (7)