Коливання та хвилі § 12. Коливальний рух

Коливальним рухом називається рух, що повторюється в часі. Якщо повторюваність відбувається за один і той же проміжок часу Т, то рух називається періодичним, а час Т  періодом. За період здійснюється одне повне коливання. Частота коливань  число повних коливань за одиницю часу,  = 2  циклічна частота. Рівняння коливання описує залежність зміщення тіла з положення рівноваги від часу.

Г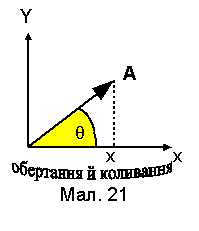 армонічним називається коливання, рівняння якого описується функцією синуса або косинуса від часу  кінематичне визначення, наприклад,

х = А·cos(t + ).

В цьому виразі х  зміщення від положення рівноваги, А  амплітуда коливань (максимальне зміщення), Ф(t)=t+  фаза коливань, Ф(t=0)=  початкова фаза. Якщо рух тіла спричиняється пружною силою, або квазипружною силою  величина сили пропорційна зміщенню тіла зі стану спокою), то такі коливання будуть також гармонічними. Це є динамічне визначення гармонічних коливань.

Гармонічне коливання можна представити графічно за допомогою вектора А, який обертається в площині ХОУ (див. Мал. 21). Модуль вектора дорівнює амплітуді коливання, а кут , який він складає з віссю ОХ дорівнює фазі коливання, тобто =Ф=t-. Проекція вектора А на вісь ОХ здійснює коливання по гармонічному закону х=А·cos(t+). Графічне зображення гармонічного коливання називається методом векторних діаграм.

В комплексній формі гармонічне коливання можна представити у вигляді:

,

де Z₀ = A·e^i  комплексна амплітуда, модуль якої дорівнює Z₀=A, а аргумент  argZ₀=. Фізичний зміст має дійсна частина комплексної величини Z, а саме , або уявна частина , які представляють гармонічні коливання величин х та y відповідно.

§ 13. Математичний маятник

Математичний маятник  точкове тіло маси m, підвішене на нерозтяжному підвісі L, розмірами якого , порівнюючи з довжиною підвісу, можна знехтувати. Маса підвісу значно менша маси тіла m. Коливання описуються кутом відхилення тіла від положення рівноваги  . Вектор задає точку прикладання сил. Коливання здійснюються в загальному випадку під дією моменту зовнішніх сил , моменту сили тяжіння та моменту сил опору , де  коефіцієнт опору. Вектори моментів сил та кутового прискорення лежать на осі обертання, яка  площині коливання та проходить через центр обертання О.

В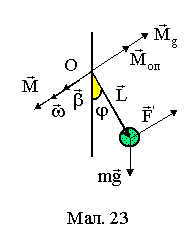 еличину моменту сили тяжіння можна записати у вигляді . Для малих коливань  маємо sin­   і . За другим законом Ньютона для обертового руху маятника рівняння коливань можна записати так

,

де J=mL²  момент інерції точкового тіла. Вектори лежать на одній прямій, а тому, взявши напрямок кутового прискорення за додатній , векторне рівняння можна записати в алгебраїчній формі

.

В канонічному вигляді це рівняння має вигляд:

,

де  коефіцієнт згасання коливань, , ₀  частота вільних незгасаючих коливань, або частота власних коливань маятника.

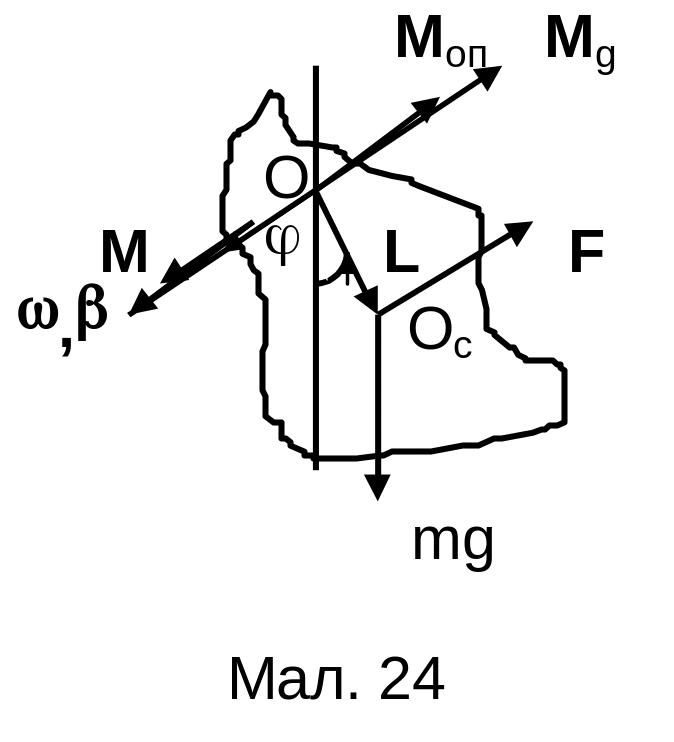
§ 14. Фізичний маятник

Фізичний маятник  макроскопічне тіло, що здійснює малі періодичні коливання. Вісь обертання маятника О зміщена відносно центра мас тіла O_c на вектор . Коливання визначаються кутом  відхилення тіла від положення рівноваги. Ці коливання здійснюються в загальному випадку під дією моменту зовнішніх сил , моменту сили тяжіння та моменту сил опору , де  коефіцієнт опору. Величину моменту сили тяжіння можна записати у вигляді: М_g = mgLsin. Для малих коливань маятника маємо sin­   і М_g = mgL.

Використовуючи другий закон Ньютона для обертового руху, рівняння коливань можна записати так:

, (1)

де J  момент інерції тіла. Вектори лежать на одній прямій, а тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати в алгебраїчній формі:

. (2)

В канонічному вигляді рівняння (2) можна записати так

, (3)

де  коефіцієнт згасання коливань, , ₀  частота вільних незгасаючих коливань. Період малих власних коливань маятника T₀ = 2/₀ і T₀ = 2 , де l_пр =  приведена^)* довжина фізичного маятника.