
- •Застосування статистичних методів та методу найменших квадратів у фізичних вимірюваннях
- •Приклад 1
- •Хід виконання статистичної обробки прямих вимірювань.
- •5.Співвідношення величин та s.
- •6.Границі довірчого інтервалу .
- •Хід виконання статистичної обробки непрямих вимірювань.
- •1.Обчислення середнього значення густини.
- •Дослідження закону збереження імпульсу й визначення коефіцієнта відновлення енергії
- •Хід виконання роботи Завдання 1. Пружне зіткнення куль.
- •Методика обробки результатів вимірювання
- •З авдання 2. Не пружне зіткнення куль
- •Методика обробки результатів вимірювання
- •Контрольні питання
- •Вивчення законів обертового руху на прикладі маятника обербека
- •Визначення моменту сил тертя.
- •2. Визначення моменту інерції маятника.
- •Хід виконання роботи. Завдання 1. Вимірювання моменту сили тертя
- •Результати вимірів занести в Таблицю 1.
- •Завдання 2. Вимірювання моменту інерції маятника.
- •Завдання 3. Визначення моменту інерції маятника j0 .
- •Контрольні питання
- •Визначення моменту інерції тіла методом крутильних коливань
- •Хід виконання роботи
- •Вимірювання прискорення сили тяжіння за допомогою математичного маятника
- •Х ід виконання роботи
- •Методика обробки результатів вимірювання
- •Визначення характеристик вільних згасаючих коливань фізичного маятника
- •Х ід виконання роботи
- •Методика обробки результатів вимірювання
- •Визначення швидкості звуку та сталої адіабати у повітрі
- •Хід виконання роботи
- •Обробка результатів вимірів.
- •Контрольні питання
- •Хід виконання роботи.
- •Обробка результатів вимірів
- •Термодинаміка
- •Лабораторна робота № 12
- •Визначення деяких молекулярно-кінетичних характеристик повітря
- •Мета роботи.
- •Прилади та обладнання
- •Коротка теорія.
- •Хід виконання роботи
- •О бробка результатів вимірювання Обчислити
- •Визначення коефіцієнта в'язкості рідини методом Стокса.
- •Визначення сталої адіабати повітря атмосфери.
- •Х ід виконання роботи та обробка результатів вимірювання.
- •Методика обробки результатів вимірювання
- •Визначення коефіцієнта поверхневого натягу рідини
- •Хід виконання роботи
- •Визначення сталої Больцмана
- •Хід виконання роботи
- •Методика обробки результатів вимірювання
- •Контрольні запитання
- •Додаток Механіка § 1. Основні поняття механіки
- •§ 2. Швидкість
- •§ 3. Прискорення, кривина траєкторії
- •§ 4. Кінематика обертового руху
- •§ 5. Закони Ньютона
- •§ 6. Імпульс тіла та імпульс сили. Закон збереження імпульсу
- •§ 7. Робота сили та її обчислення. Потужність. Енергія
- •§ 8. Закон збереження енергії
- •§ 9. Центральний удар двох не взаємодіючих куль
- •§ 10. Динаміка обертового руху
- •§ 11. Другий закон Ньютона для обертового руху
- •§ 12. Момент інерції деяких тіл
- •§ 13. Маятник Обербека
- •Коливання та хвилі § 12. Коливальний рух
- •§ 13. Математичний маятник
- •§ 14. Фізичний маятник
- •§ 15. Крутильний маятник
- •§ 16. Вільні незгасаючі коливання
- •§ 17. Вільні згасаючі коливання
- •§ 18. Характеристики вільних згасаючих коливань
- •§ 19. Стоячі хвилі
- •§ 20. Спектр власних частот одновимірних середовищ
- •§ 21. Ультразвук
- •Статистична фізика та термодинаміка § 22. Cередня довжина вільного пробігу частинки ідеального газу
- •§ 23. Явища переносу
- •§ 24. Ідеальний газ та термодинамічні процеси в ньому
- •§ 25. Теорема Больцмана про рівнорозподіл енергії
- •§ 26. Робота термодинамічної системи
- •§ 27. Перший закон (начало) термодинаміки
- •§ 28. Адіабатичний процес
- •§ 29. Теплоємність ідеального газу
- •§ 30. Рідини
- •4. Стискальність
- •§ 31. Стаціонарна течія рідини та газу в циліндрі
§ 11. Другий закон Ньютона для обертового руху
Візьмемо похідну
від
![]() по часу
по часу
![]() .
(1)
.
(1)
Перший доданок у
правій частині (1) дорівнює 0, тому що
маємо векторний добуток паралельних
векторів - швидкості тіла та його
імпульсу. У другому доданкові за другим
законом Ньютона
![]() .
Тепер остаточно маємо
.
Тепер остаточно маємо
![]() .
(2)
.
(2)
Підставивши в (2) вираз для моменту імпульсу одержимо
![]() .
(3)
.
(3)
Прирівнюючи праві частини (2) та (3), одержимо
![]() .
(4)
.
(4)
Вирази (3) та (4)
представляють собою рівняння другого
закону Ньютона для обертового руху. З
(4) можна зробити висновок про фізичний
зміст моменту інерції J,
а саме, момент інерції є мірою інертності
тіла відносно моменту сили, що діє на
нього. При дії на тіло моменту сили
![]() воно буде обертатися з більшим кутовим
прискоренням
при меншому моментові інерції J.
воно буде обертатися з більшим кутовим
прискоренням
при меншому моментові інерції J.
§ 12. Момент інерції деяких тіл
Момент інерції
макроскопічного тіла можна знайти
розбиттям тіла на нескінченно малі маси
![]() і розглянути їх як точкові. При цьому
момент інерції тіла дорівнює сумі
моментів інерції його складових
і розглянути їх як точкові. При цьому
момент інерції тіла дорівнює сумі
моментів інерції його складових
![]()
або
![]() .
.
Застосовуючи цей метод, розглянемо момент інерції деяких тіл.
а). Момент інерції
J тонкого обруча
маси m і радіусом R
відносно осі, що проходить через центр,
перпендикулярно його площині, дорівнює
J=mR2.
Дійсно, якщо розбити обруч на нескінченно
малі дуги з масами dm, які
мають радіус обертання
![]() ,
то
,
то
![]() .
При R=0, J=0 і
тоді С=0, а
.
При R=0, J=0 і
тоді С=0, а
![]() .
.
б). Момент інерції J циліндра маси m із радіусом основи R відносно його осі дорівнює J=mR2/2.
Дійсно, розіб'ємо циліндр на концентричні обручі радіуса х з нескінченно малою товщиною dx момент інекції яких буде дорівнювати dJ=x2dm, де dm=2xdxh елемент маси обруча, h висота циліндра, його густина. Тепер момент інерції циліндра можна обчислити так:
![]()
J=![]() hR4=
(R2h)R2=
hR4=
(R2h)R2=
![]() mR2.
mR2.
Момент інерції J диска маси m із радіусом основи R відносно осі, що проходить через центр мас, перпендикулярно його площині, дорівнює J= mR2. Ми зважили, що диск за формою є циліндром.
в). Момент інерції циліндричного кільця маси m з внутрішнім радіусом R1 і зовнішнім R2 відносно його осі дорівнює:
 ,
,
![]()
і остаточно
![]() ,
,
де
![]() маса циліндра з
радіусом основи R1,
маса циліндра з
радіусом основи R1,
![]() маса циліндра з
радіусом основи R2,
а m=m2-m1-маса
кільця.
маса циліндра з
радіусом основи R2,
а m=m2-m1-маса
кільця.
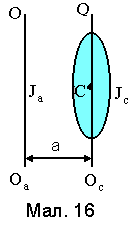
Теорема Штейнера: момент інерції Ja тіла відносно осі ООа паралельній осі ООс, яка проходить через центр мас тіла на відстані а від неї, дорівнює Ja=Jc+ma2, де Jc момент інерції тіла відносно осі ООс (див. Мал. 16).
§ 13. Маятник Обербека
Для ілюстрації сумісного розв'язку рівнянь поступального та обертового руху, розглянемо маятник Обербека. Маятник Обербека являє собою циліндричне тіло із шківом на осі радіусу r та 4-ма однаковими взаємно перпендикулярними стержнями. На стержнях пристосовані пересувні тягарці масою m0 кожний. Вони розташовані на відстані R від центру маятника (див. Мал. 17).
Стержні лежать у
площині осі циліндра
і проходять через центр маятника. Маятник
приводиться в обертовий рух тягарцем
m із ниткою, намотаною на
шків. Вісь обертання співпадає з віссю
циліндра. Спочатку тягарець за рахунок
сили натягу нитки
![]() розкручує маятник на всю довжину нитки
h1 і в нижній точці
ривком маятника починає підніматися в
гору. Після підняття тягарця на висоту
h2<h1,
маятник зупиняється й починає обертовий
рух у протилежному початковому напрямкові.
розкручує маятник на всю довжину нитки
h1 і в нижній точці
ривком маятника починає підніматися в
гору. Після підняття тягарця на висоту
h2<h1,
маятник зупиняється й починає обертовий
рух у протилежному початковому напрямкові.
За час опускання t та підйому t маятник повертається на кут
![]() ,
,
д е
r
радіус шківа. Запишемо рівняння руху
тягарця та маятника, виходячи з наступного.
При опусканні тягарця, маятник приводиться
в обертовий рух моментом сили натягу
е
r
радіус шківа. Запишемо рівняння руху
тягарця та маятника, виходячи з наступного.
При опусканні тягарця, маятник приводиться
в обертовий рух моментом сили натягу
![]() ,
де
радіус-вектор
точки прикладання сили відносно центра
обертання, а момент сили тертя
,
де
радіус-вектор
точки прикладання сили відносно центра
обертання, а момент сили тертя
![]() гальмує цей рух (див. Мал. 17). Вектор
кутового прискорення
гальмує цей рух (див. Мал. 17). Вектор
кутового прискорення
![]() лежить на осі обертання і
лежить на осі обертання і
![]() ,
причому
,
причому
![]() .
Усі три вектори
.
Усі три вектори
![]() лежать
на осі обертання і тому, вибравши напрям
вектора кутового прискорення за додатній,
векторне рівняння другого закону Ньютона
для обертового руху маятника
лежать
на осі обертання і тому, вибравши напрям
вектора кутового прискорення за додатній,
векторне рівняння другого закону Ньютона
для обертового руху маятника
![]()
можна записати в алгебраїчному вигляді
![]() .
.
В цьому рівнянні
![]() модуль моменту
сили натягу підвісу.
модуль моменту
сили натягу підвісу.
При опусканні
тягарця, на нього діють прискорююча
сила тяжіння
![]() та гальмуюча сила натягу
та гальмуюча сила натягу
![]() ,
причому
,
причому
![]() .
Вектор прискорення
.
Вектор прискорення
![]() .
Усі три вектори лежать на одній прямій
і тому, вибравши за додатній напрямок
вектора прискорення, векторне рівняння
другого закону Ньютона для прискореного
руху тягарця
.
Усі три вектори лежать на одній прямій
і тому, вибравши за додатній напрямок
вектора прискорення, векторне рівняння
другого закону Ньютона для прискореного
руху тягарця
![]()
можна записати в алгебраїчному вигляді
![]() .
.
Таким чином ми одержали першу пару рівнянь руху маятника Обербека:
, (1)
![]() .
(2)
.
(2)
Рух тягарця рівноприскорений і тому
![]() .
(3)
.
(3)
Для знаходження моменту інерції маятника J, помножимо рівняння (2) на r і додамо ліві та праві частини рівнянь (1-2). В результаті одержимо
rmg-![]() .
(4)
.
(4)
Підставимо в (4)
![]() і знайдемо J:
і знайдемо J:
![]() .
(5)
.
(5)
В (5) залишається невідомим момент сили тертя. Знайдемо його з того, що робота проти сили тертя дорівнює
![]() ,
(6)
,
(6)
Робота виконується
за рахунок зменшення потенціальної
енергії тягарця на величину
![]() .
Після підстановки в (6) значень кута
повороту та енергії одержимо значення
моменту сили тертя
.
Після підстановки в (6) значень кута
повороту та енергії одержимо значення
моменту сили тертя
![]() .
(7)
.
(7)
Момент інерції J є сумою моменту інерції власне маятника J0 та моменту інерції 4-х тягарців m, які можна вважати точковими, і тоді
![]() .
(8)
.
(8)
