
- •Застосування статистичних методів та методу найменших квадратів у фізичних вимірюваннях
- •Приклад 1
- •Хід виконання статистичної обробки прямих вимірювань.
- •5.Співвідношення величин та s.
- •6.Границі довірчого інтервалу .
- •Хід виконання статистичної обробки непрямих вимірювань.
- •1.Обчислення середнього значення густини.
- •Дослідження закону збереження імпульсу й визначення коефіцієнта відновлення енергії
- •Хід виконання роботи Завдання 1. Пружне зіткнення куль.
- •Методика обробки результатів вимірювання
- •З авдання 2. Не пружне зіткнення куль
- •Методика обробки результатів вимірювання
- •Контрольні питання
- •Вивчення законів обертового руху на прикладі маятника обербека
- •Визначення моменту сил тертя.
- •2. Визначення моменту інерції маятника.
- •Хід виконання роботи. Завдання 1. Вимірювання моменту сили тертя
- •Результати вимірів занести в Таблицю 1.
- •Завдання 2. Вимірювання моменту інерції маятника.
- •Завдання 3. Визначення моменту інерції маятника j0 .
- •Контрольні питання
- •Визначення моменту інерції тіла методом крутильних коливань
- •Хід виконання роботи
- •Вимірювання прискорення сили тяжіння за допомогою математичного маятника
- •Х ід виконання роботи
- •Методика обробки результатів вимірювання
- •Визначення характеристик вільних згасаючих коливань фізичного маятника
- •Х ід виконання роботи
- •Методика обробки результатів вимірювання
- •Визначення швидкості звуку та сталої адіабати у повітрі
- •Хід виконання роботи
- •Обробка результатів вимірів.
- •Контрольні питання
- •Хід виконання роботи.
- •Обробка результатів вимірів
- •Термодинаміка
- •Лабораторна робота № 12
- •Визначення деяких молекулярно-кінетичних характеристик повітря
- •Мета роботи.
- •Прилади та обладнання
- •Коротка теорія.
- •Хід виконання роботи
- •О бробка результатів вимірювання Обчислити
- •Визначення коефіцієнта в'язкості рідини методом Стокса.
- •Визначення сталої адіабати повітря атмосфери.
- •Х ід виконання роботи та обробка результатів вимірювання.
- •Методика обробки результатів вимірювання
- •Визначення коефіцієнта поверхневого натягу рідини
- •Хід виконання роботи
- •Визначення сталої Больцмана
- •Хід виконання роботи
- •Методика обробки результатів вимірювання
- •Контрольні запитання
- •Додаток Механіка § 1. Основні поняття механіки
- •§ 2. Швидкість
- •§ 3. Прискорення, кривина траєкторії
- •§ 4. Кінематика обертового руху
- •§ 5. Закони Ньютона
- •§ 6. Імпульс тіла та імпульс сили. Закон збереження імпульсу
- •§ 7. Робота сили та її обчислення. Потужність. Енергія
- •§ 8. Закон збереження енергії
- •§ 9. Центральний удар двох не взаємодіючих куль
- •§ 10. Динаміка обертового руху
- •§ 11. Другий закон Ньютона для обертового руху
- •§ 12. Момент інерції деяких тіл
- •§ 13. Маятник Обербека
- •Коливання та хвилі § 12. Коливальний рух
- •§ 13. Математичний маятник
- •§ 14. Фізичний маятник
- •§ 15. Крутильний маятник
- •§ 16. Вільні незгасаючі коливання
- •§ 17. Вільні згасаючі коливання
- •§ 18. Характеристики вільних згасаючих коливань
- •§ 19. Стоячі хвилі
- •§ 20. Спектр власних частот одновимірних середовищ
- •§ 21. Ультразвук
- •Статистична фізика та термодинаміка § 22. Cередня довжина вільного пробігу частинки ідеального газу
- •§ 23. Явища переносу
- •§ 24. Ідеальний газ та термодинамічні процеси в ньому
- •§ 25. Теорема Больцмана про рівнорозподіл енергії
- •§ 26. Робота термодинамічної системи
- •§ 27. Перший закон (начало) термодинаміки
- •§ 28. Адіабатичний процес
- •§ 29. Теплоємність ідеального газу
- •§ 30. Рідини
- •4. Стискальність
- •§ 31. Стаціонарна течія рідини та газу в циліндрі
§ 2. Швидкість
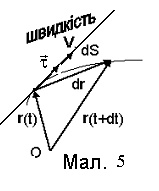
Рух тіла в різні моменти часу може відрізнятися величиною та напрямом переміщення. Для визначення цих змін, вводиться поняття швидкості тіла.
Швидкість (миттєва швидкість) - це вектор, який дорівнює похідній від радіус-вектора положення тіла в просторі по часу
![]() .
.
Величина швидкості
![]() (величина миттєвої швидкості) є похідною
від шляху, пройденого тілом по часу
(величина миттєвої швидкості) є похідною
від шляху, пройденого тілом по часу
![]() .
Ми зважили на той факт, що нескінченно
мала дуга кола дорівнює довжині хорди,
що стягує цю дугу |dr|=dS,
і тоді
.
Ми зважили на той факт, що нескінченно
мала дуга кола дорівнює довжині хорди,
що стягує цю дугу |dr|=dS,
і тоді
![]() .
Вектор швидкості лежить на дотичній до
траєкторії, так як
.
Вектор швидкості лежить на дотичній до
траєкторії, так як
![]() (див. Мал. 5).
(див. Мал. 5).
Середня швидкість
- вектор, який дорівнює відношенню
вектора переміщення r
тіла в просторі до скінченого проміжку
часу t,
за який це переміщення сталося
![]() .
.
Середня за величиною
швидкість нерівномірного руху
дорівнює відношенню шляху
![]() ,
пройденого тілом до часу руху
,
пройденого тілом до часу руху
![]()
![]() ,
,
тобто це є швидкість такого рівномірного прямолінійного руху, коли за час t тіло проходить шлях S.
Одиницею вимірювання швидкості є м/с.
Рух тіла може бути зі сталою швидкістю - рівномірний і прямолінійний, із швидкістю, що змінюється за величиною й напрямком - прискорений, криволінійний рух.
§ 3. Прискорення, кривина траєкторії
Прискорення
криволінійного руху визначає зміну
швидкості за напрямом та величиною.
Прискорення (миттєве прискорення)
- вектор, який є похідною від швидкості
тіла по часу
![]() .
Кут між прискоренням матеріальної
точки, що рухається по кривій, і її
швидкістю може змінюватися від 0 до 180
градусів. Одиницею вимірювання прискорення
є
.
Кут між прискоренням матеріальної
точки, що рухається по кривій, і її
швидкістю може змінюватися від 0 до 180
градусів. Одиницею вимірювання прискорення
є
![]() .
.
С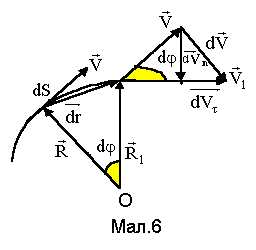 ереднє
прискорення - вектор, який дорівнює
відношенню приросту швидкості V
до часу t,
за який цей приріст стався
ереднє
прискорення - вектор, який дорівнює
відношенню приросту швидкості V
до часу t,
за який цей приріст стався
![]() .
.
Прискорення визначає
зміну вектора швидкості
![]() за величиною - тангенціальна складова
прискорення
за величиною - тангенціальна складова
прискорення
![]() та за напрямком - нормальна складова
та за напрямком - нормальна складова
![]() .
Розглянемо докладніше це питання.
Швидкості
та
.
Розглянемо докладніше це питання.
Швидкості
та
![]() є дотичними до траєкторії (див.
Мал. 6) і точка перетину нормалей до
них визначає центр кола О, дуга якого
dS співпадає з траєкторією
dS. За радіус кола можна
взяти R чи R1,
величини яких практично однакові і які
називаються радіусами кривизни
траєкторії. Приріст вектора швидкості
dV можна
розкласти на два вектори: по нормалі -
dVn
та по дотичній до траєкторії - dV.
Ці складові називаються нормальною та
тангенціальною відповідно. Вектор
прискорення тепер можна записати у
вигляді а=an+а,
де
є дотичними до траєкторії (див.
Мал. 6) і точка перетину нормалей до
них визначає центр кола О, дуга якого
dS співпадає з траєкторією
dS. За радіус кола можна
взяти R чи R1,
величини яких практично однакові і які
називаються радіусами кривизни
траєкторії. Приріст вектора швидкості
dV можна
розкласти на два вектори: по нормалі -
dVn
та по дотичній до траєкторії - dV.
Ці складові називаються нормальною та
тангенціальною відповідно. Вектор
прискорення тепер можна записати у
вигляді а=an+а,
де
![]() - нормальне i
- нормальне i
![]() -
тангенціальне прискорення. З малюнка
видно, що dVn=Vd,
а
-
тангенціальне прискорення. З малюнка
видно, що dVn=Vd,
а
![]() і тому
і тому
![]()
Кривина траєкторії
за визначенням є С=![]() ,
d
- кутова величина дуги dL.
Для малих d
маємо dS=R·d
i кривина траєкторії
може бути записана у вигляді
,
d
- кутова величина дуги dL.
Для малих d
маємо dS=R·d
i кривина траєкторії
може бути записана у вигляді
![]() .
.
§ 4. Кінематика обертового руху
Обертовий рух точки (див. Мал. 7) визначається кутом повороту радіус-вектора положення тіла r(t). Елементарний поворот d визначається як вектор, що лежить на осі обертання, причому обертання тіла відбувається проти годинникової стрілки, якщо його спостерігати з кінця вектора d.
Цей вектор задовольняє аксіомам алгебри векторів. Однак, скінчені повороти не задовольняють цим аксіомам і не можуть представлятися векторами. Вектор переміщення dr за величиною можна визначити як dr=rd.
К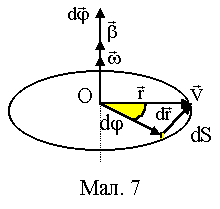 утова
швидкість є похідною від кута повороту
радіус-вектора r(t)
утова
швидкість є похідною від кута повороту
радіус-вектора r(t)
![]() ,
,
її вектор лежить на
вісі обертання і паралельний вектору
![]() .
Кутове прискорення
.
Кутове прискорення
![]() визначається як
визначається як
![]()
і є вектором, паралельним вектору кутової швидкості.
Одиницею вимірювання
величини кутової швидкості є
![]() ,
а кутового прискорення -
,
а кутового прискорення -
![]() .
.
Лінійна швидкість
V обертового руху
дорівнює векторному добуткові кутової
швидкості
![]()
![]()
і радіуса обертання
:
і радіуса обертання
:
![]() .
Дійсно, величина швидкості V=
.
Дійсно, величина швидкості V=![]() , а за напрямком
.
, а за напрямком
.
Величина тангенціального
прискорення обертового руху дорівнює
добуткові кутового прискорення
i радіуса кривизни r
a=r.
Дійсно, a=![]() =
=
![]() =r·
=r·![]() =r
(r=const) , причому
=r
(r=const) , причому
![]() .
.
Час повного обороту (кут обертання 360 градусів) називається періодом T, а число повних оборотів за одиницю часу - частотою n=1/T, причому кут повороту за одиницю часу = 2n. Одиницею вимірювання швидкості є рад/c, а прискорення - рад/c2.
