Визначення сталої адіабати повітря атмосфери.

Мета роботи .

Обчислити сталу адіабати атмосферного повітря.

Прилади та обладнання

• балон,

• манометр,

• насос,

• 2 крани.

Коротка теорія.

Статистичний метод дозволяє розрахувати теплоємність ідеального газу. В Додатку (§§ 24, 25, 28) докладно розглянуто внутрішню енергію ідеального газу та його теплоємності у різних процесах. Наведемо деякі, потрібні в роботі результати, одержані у вказаних параграфах.

Молярна теплоємність при сталому об’ємі дорівнює

, (1)

а при сталому тискові

(2)

У виразах (1-2) і  число ступенів свободи молекули.

Відношення вказаних теплоємкостей

(3)

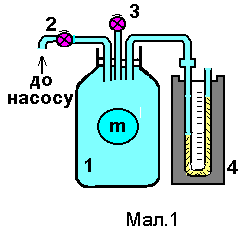
називається сталою адіабати. Для визначення величини  застосувується установка, принципова схема якої наведена на Мал.1. Вона складається зі скляного балона 1, з’єднаного із манометром 4 і насосом. За допомогою крану 3 балон може сполучатись з атмосферою, а краном 2  із насосом.

Представимо, що у середині балона виділено якусь масу газу m. Саме її і будемо досліджувати у описуваних нижче процесах і саме до цієї маси будемо застосовувати закони термодинаміки.

Приймемо, що у початковий момент газ знаходиться у стані де Р₁  атмосферний тиск газу, V₁  початковий об’єм газу, Т₁  температура атмосферного повітря у кімнаті. Проведемо з виділеним газом експеримент, принципова схема якого зображена у діаграмі на Мал. 2.

1. Закриємо кран 3 і відкриємо кран 2. Накачаємо насосом у балон деяку додаткову масу газу і закриємо кран 2. При цьому газ із стану перейде у стан . Його тиск і температура збільшаться до і . Зачекаємо деякий час , поки температура у балоні зменшиться до атмосферної, а тиск стане рівним Р₂, тобто газ перейде у стан .

Зміна тиску у досліді вимірюється різницею висот стовпа рідини водяного манометра h. Прийнявши тиск атмосфери рівним висоті Н водяного стовпа, тиск Р₂ запишеться як .

2. Відкриємо на короткий час кран 3. При цьому газ адіабатично перейде зі стану у стан , причому його температура зменшиться до Т₃, об’єм збільшиться до V₃, а тиск стане рівний атмосферному Р₁. Стани 3 та 4 зв’язані рівнянням адіабати

. (4)

Через деякий час температура газу Т₃ шляхом теплообміну через стінки балона підвищиться до температури атмосфери Т₁, а тиск збільшиться до Р₃ і газ перейде у стан . Стани 4 та 5 знаходяться на одній ізотермі і тому

. (5)

Тиск Р₃ запишемо у вигляді . З рівнянь (4) і (5) утворимо рівняння

. (6)

Підставивши у формулу (6) тиски, виражені через перепад висот водяного манометра, одержимо рівняння, для визначення сталої адіабати

. (7)

Після логарифмування виразу (7) одержимо

Нагадаємо у який спосіб можна спростити вираз (7), коли .

Похідною функції y=f(x) за визначенням є

. (9)

Для достатньо малих х похідну з достатньою точністю можна обчислити наближено як

. (10)

З останнього виразу можна наближено знайти значення функції у точці х+х через значення функції та її похідної у точці х та х:

f(х+х)=f(x)+ ·x= f(x)+ ·x = f(x)+ f'(x)·x (11)

У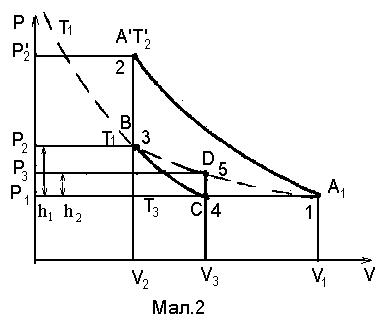 виразі (7) під знаком логарифма стоїть аргумент H+h, причому відношення тому, що величина стовпа води а величини . Користуючись виразом (11) можна записати

, . (12)

Підставляючи (12) у (7) одержимо остаточний вираз для обчислення сталої адіабати

. (13)