25. Частота столкновений молекул идеального газа. Средняя длина свободного пробега газовых молекул.

Молекулы, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь l,

который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но т. к. мы имеем дело с огромным числом хаотически движущихся молекул, то можно говорить о средней длине свободного пробега молекул <l>.

Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d. (рис.1). Он зависит от скорости сталкивающихся молекул, т.е. от температуры газа (несколько уменьшается с ростом температуры).

Так как за 1 с молекула проходит в среднем путь, равный средней арифметической скорости <v>, и если <z> — среднее число столкновений, испытываемых одной молекулой газа за 1 с, то

средняя длина свободного пробега <l>=<v>/<z>.

Рис.1 рис.2

Для определения <z> представим молекулу в виде шарика радиусом d, которая движется среди других «застывших» молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри «ломаного» цилиндра диаметром d(рис. 2).

Среднее число столкновений за 1 с равно числу молекул в объеме «ломаного» цилиндра:<z>=nV, где n-концентрация молекул, V =d² <v>, <v>— средняя скорость молекулы или путь, пройденный ею за 1 с. Таким образом, среднее число столкновений <z>=nd² <v>.

Предположение о том, что все молекулы, кроме одной, неподвижны, является не верным. В действительности все молекулы движутся, и возможность соударения двух частиц зависит от их относительной скорости. Поэтому вместо среднеарифметической скорости <v> должны входить средняя относительная скорость молекул <v_отн>. Если скорости молекул распределены по закону Максвелла, то, как можно показать, средняя относительная скорость двух молекул однородного газа в раз превышает . Таким образом, среднее число соударений должно быть увеличено в раз, <z>=n=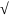 2d² <v>.

Тогда средняя длина свободного пробега <l>=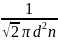 , т.е. <l> обратно пропорциональна концентрации п молекул. С другой стороны, из уравнения p=nkT следует, что при постоянной температуре п пропорциональна давлению р. Следовательно, .

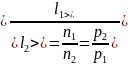Таким образом, средняя длина свободного пробега не зависит от температуры газа, т.к. с ростом температуры одновременно возрастают и <v>, и <z>. При подсчете числа соударений и средней длины свободного пробега молекул за модель молекулы было принято шарообразное упругое тело. В действительности каждая молекула представляет собой сложную систему элементарных частиц и при рассмотрении упругого соударения молекул имелось в виду, что центры молекул могут сблизиться до некоторого наименьшего расстояния. Затем возникает силы отталкивания которые вызывают взаимодействие, подобное взаимодействию при упругом ударе.